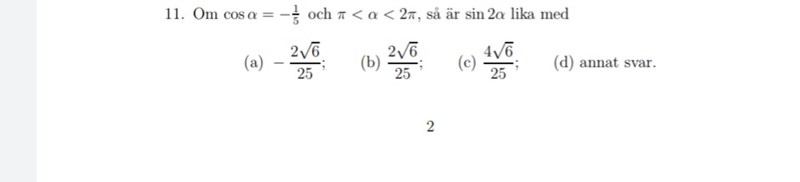Hur tänker du?
henrikus skrev:Hur tänker du?
Jag fick+- 2*roten ur 6/5. Sin2x= 2*(2rotenur6/5)=4*roten ur 6/5. Jag fattar ej varför jag ej kan få 25 i nämnare..
Det första jag skulle göra är att rita upp enhetscirkeln och markera vinkeln. Då kan jag klura ut i vilken kvadrant vinkeln ligger i.
Hur gjorde du för att få fram ditt svar? Vilken formel har du använt? Vilket värde har ?
Smaragdalena skrev:Det första jag skulle göra är att rita upp enhetscirkeln och markera vinkeln. Då kan jag klura ut i vilken kvadrant vinkeln ligger i.
Hur gjorde du för att få fram ditt svar? Vilken formel har du använt? Vilket värde har ?
det gjorde jag. den ligger i andra kvadranten. jag använde trigonometriska ettan
sin²x+cos²x= 1
sin²x= 1-cos²x
sin²x= 1-(-1/5)²
sin²x= 1-1/25
sin²x= 24/25
sinx= +-=
Ja, vinkeln ligger i andra kvadranten, men det jag frågade efter var i vilken kvadrant man hittar vinkeln .
Vilken formel använder du för att beräkna om du vet och ?
Smaragdalena skrev:Ja, vinkeln ligger i andra kvadranten, men det jag frågade efter var i vilken kvadrant man hittar vinkeln .
Vilken formel använder du för att beräkna om du vet och ?
okej jag vet faktiskt ej var vinkeln 2alfa kan ligga nånstans och misstänker att den kan ligga i andra kvadranten också, men sin2x är samma sak som 2sinxcosx. Om vi vet att cosx= -1/5 och sinx= så blir det 2*(*(-))
okej jag vet faktiskt ej var vinkeln 2alfa kan ligga nånstans och misstänker att den kan ligga i andra kvadranten också, m
Lägg upp din bild av enhetscirkeln, så kan vi hjälpa dig att se det.
Smaragdalena skrev:
okej jag vet faktiskt ej var vinkeln 2alfa kan ligga nånstans och misstänker att den kan ligga i andra kvadranten också, m
Lägg upp din bild av enhetscirkeln, så kan vi hjälpa dig att se det.
Nu ser jag att jag har skrivit lite fel innan...
Du har markerat fel vinkel som . Vinkeln skall börja på positiva x-axeln.
Markera intervallet . Då har du bara ett värde kvar på vinkeln.
Smaragdalena skrev:Nu ser ja gatt jag har skrivit lite fel innan...
Markera intervallet . Då har du bara ett värde kvar på vinkeln.
var ska jag markera det menar du?
Mahiya99 skrev:Smaragdalena skrev:Nu ser ja gatt jag har skrivit lite fel innan...
Markera intervallet . Då har du bara ett värde kvar på vinkeln.
var ska jag markera det menar du?
Markera det i enhetscirkeln. Såg du det jag skrev om vinkeln i mitt förra inlägg?
Smaragdalena skrev:Mahiya99 skrev:Smaragdalena skrev:Nu ser ja gatt jag har skrivit lite fel innan...
Markera intervallet . Då har du bara ett värde kvar på vinkeln.
var ska jag markera det menar du?
Markera det i enhetscirkeln. Såg du det jag skrev om vinkeln i mitt förra inlägg?
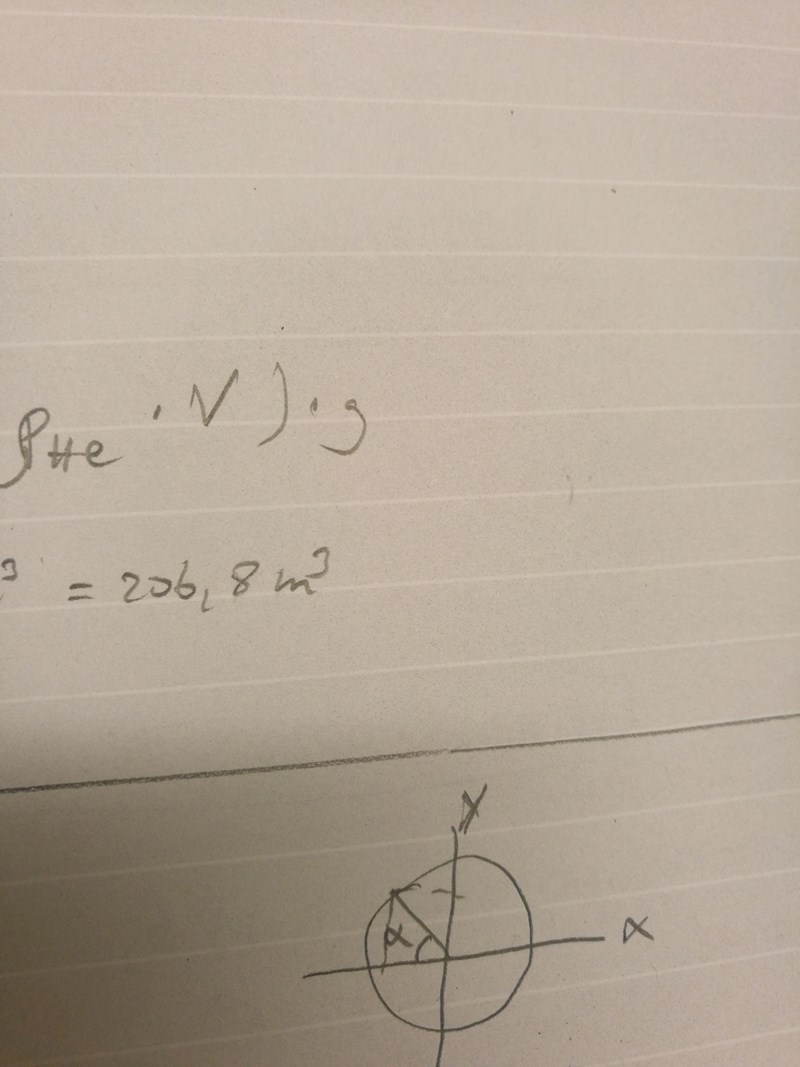
Nej. Var i enhetscirkeln har du det önskade intervallet, alltså mellan pi och 2 pi?
Smaragdalena skrev:
Nej. Var i enhetscirkeln har du det önskade intervallet, alltså mellan pi och 2 pi?
mellan tredje och fjärde kvadranten. Detta innebär väl att sinus alfa= -
Nja, hela tredje och fjärde kvadranten. Vinkeln ligger i någon av de här båda kvadrantern, och har cosinusvärdet -0,2. Markera vinkeln !
Smaragdalena skrev:Nja, hela tredje och fjärde kvadranten. Vinkeln ligger i någon av de här båda kvadrantern, och har cosinusvärdet -0,2. Markera vinkeln !
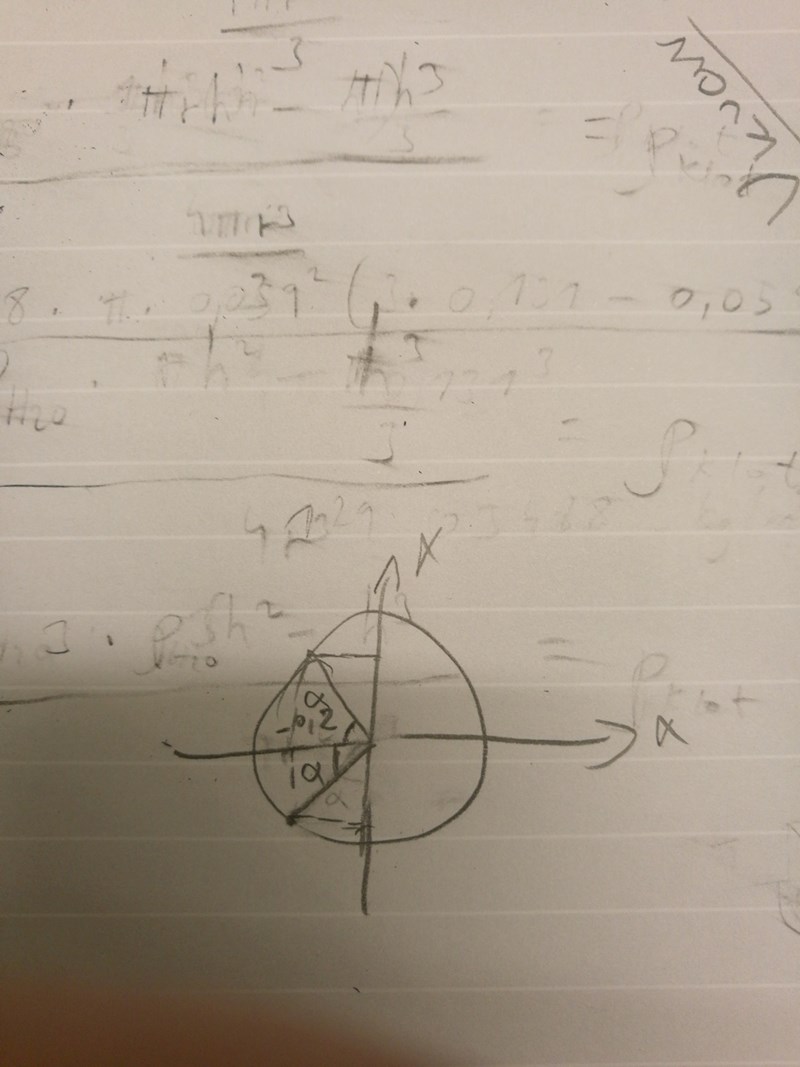
Jag vet ej om jag gjort rätt, menar du så?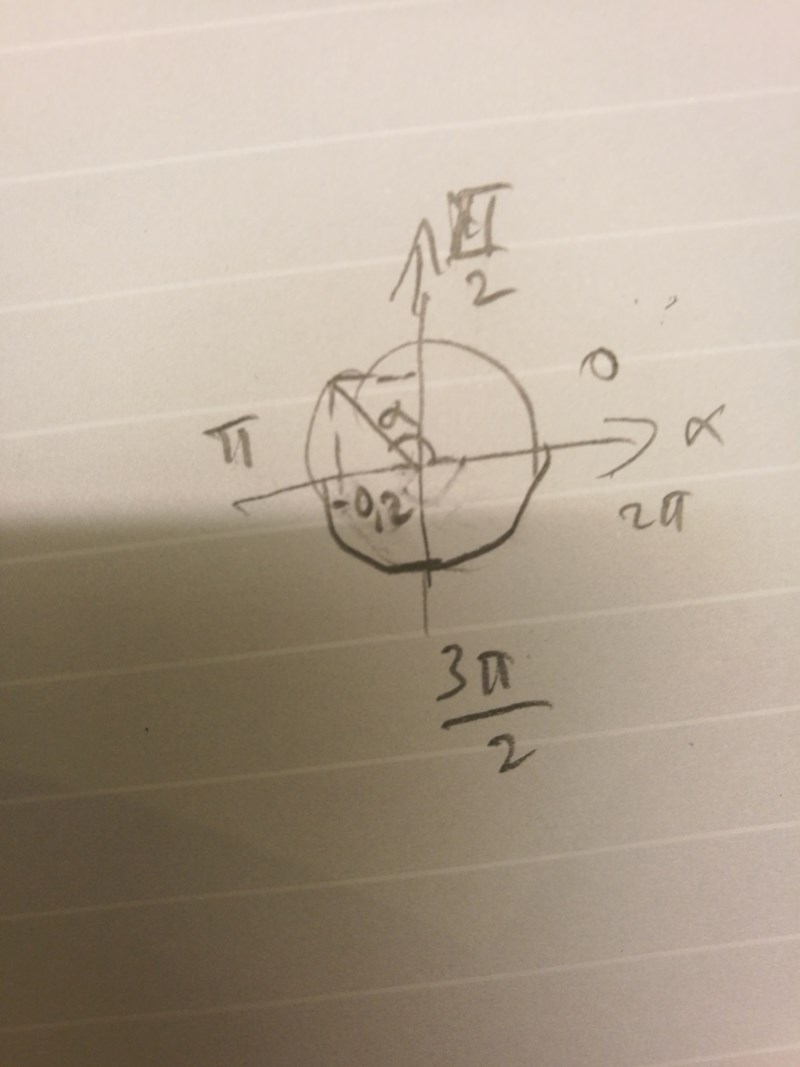
Smaragdalena skrev:Nja, hela tredje och fjärde kvadranten. Vinkeln ligger i någon av de här båda kvadrantern, och har cosinusvärdet -0,2. Markera vinkeln !
Du får gärna visa mig hur du menar med en figur så får jag lära mig något av det. Jag förstår att pi och 2pi ligger i hela tredje och fjärde kvadranten och kan tänka mig att - 0,2 måste också ligga i tredje kvadranten eftersom då blir sin alfa negativt och vi får ett svar som liknar alternativ c enligt sin2x=2 sinxcosx
Nej, din vinkel skall hamna i tredje kvadranten. Vinkeln som duhar ritat ligger i andra kvadranten, där vinkeln ligger mellan pi/2 och pi. Förläng din streckade lodräta linje tills den träffar cirkeln. Dra en linje från denna punkt till origo. Markera vinkeln , som är drygt ½ varv stor och skall ritas från positiva x-axeln genom första, andra och lite av tredje kvadranten. Lägg upp din bild.
Jag tror att du lär dig bättre om du gör det här själv, jämfört med om jag visar dig.
Smaragdalena skrev:Nej, din vinkel skall hamna i tredje kvadranten. Vinkeln som duhar ritat ligger i andra kvadranten, där vinkeln ligger mellan pi/2 och pi. Förläng din streckade lodräta linje tills den träffar cirkeln. Dra en linje från denna punkt till origo. Markera vinkeln , som är drygt ½ varv stor och skall ritas från positiva x-axeln genom första, andra och lite av tredje kvadranten. Lägg upp din bild.
Jag tror att du lär dig bättre om du gör det här själv, jämfört med om jag visar dig.
Ok jag förstår. Se bilden nedan. Jag hoppas nu att jag gjort rätt. Anledningen till att jag ritade vinkeln i andra kvadranten också är för att visa att de är spegel vända
Den undre punkten på enhetscirkeln är rätt, men du har inte markerat rätt vinkel. Vinklen skall gå hela vägen från positva x-axeln till linjen som lutar så här: /.
Smaragdalena skrev:Den undre punkten på enhetscirkeln är rätt, men du har inte markerat rätt vinkel. Vinklen skall gå hela vägen från positva x-axeln till linjen som lutar så här: /.
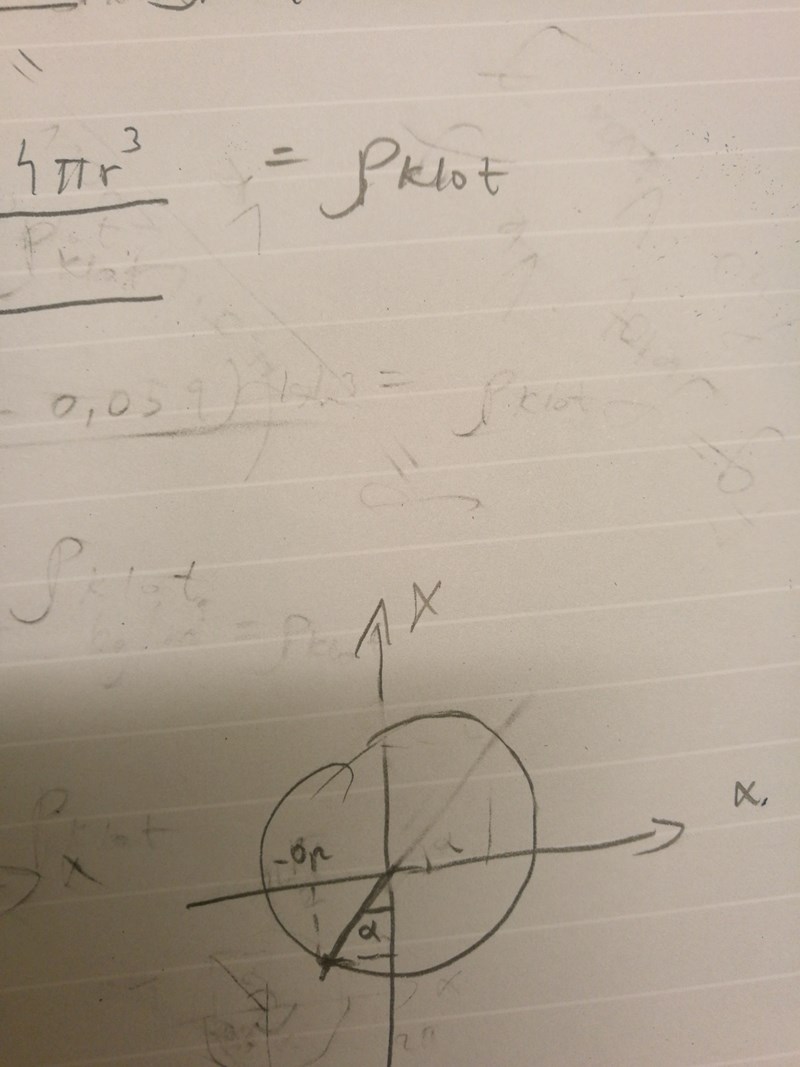
Nej. Börja på positiva x-axeln, t ex i punkten (0,5;0). Rita en cirkelbåge genom första kvadranten (du hamnar i punkten (0;0,5)). Rita en cirkelbåge genom andra kvadranten (du hamnar i punkten (-0,5;0)). Förläng cirkelbågen en bit till, tills du kommer fram till linjen som lutar så här: /.
Smaragdalena skrev:Nej. Börja på positiva x-axeln, t ex i punkten (0,5;0). Rita en cirkelbåge genom första kvadranten (du hamnar i punkten (0;0,5)). Rita en cirkelbåge genom andra kvadranten (du hamnar i punkten (-0,5;0)). Förläng cirkelbågen en bit till, tills du kommer fram till linjen som lutar så här: /.
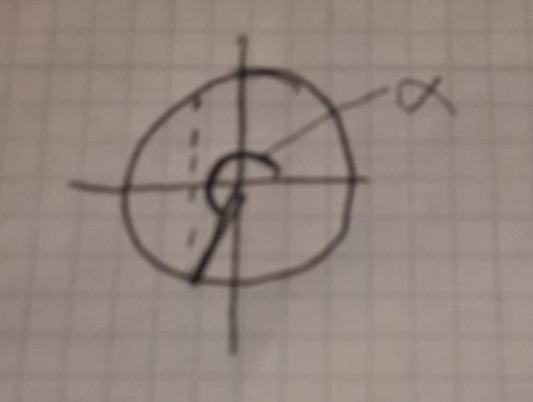
Jag ritade såhär utefter vad jag tror att du menar. 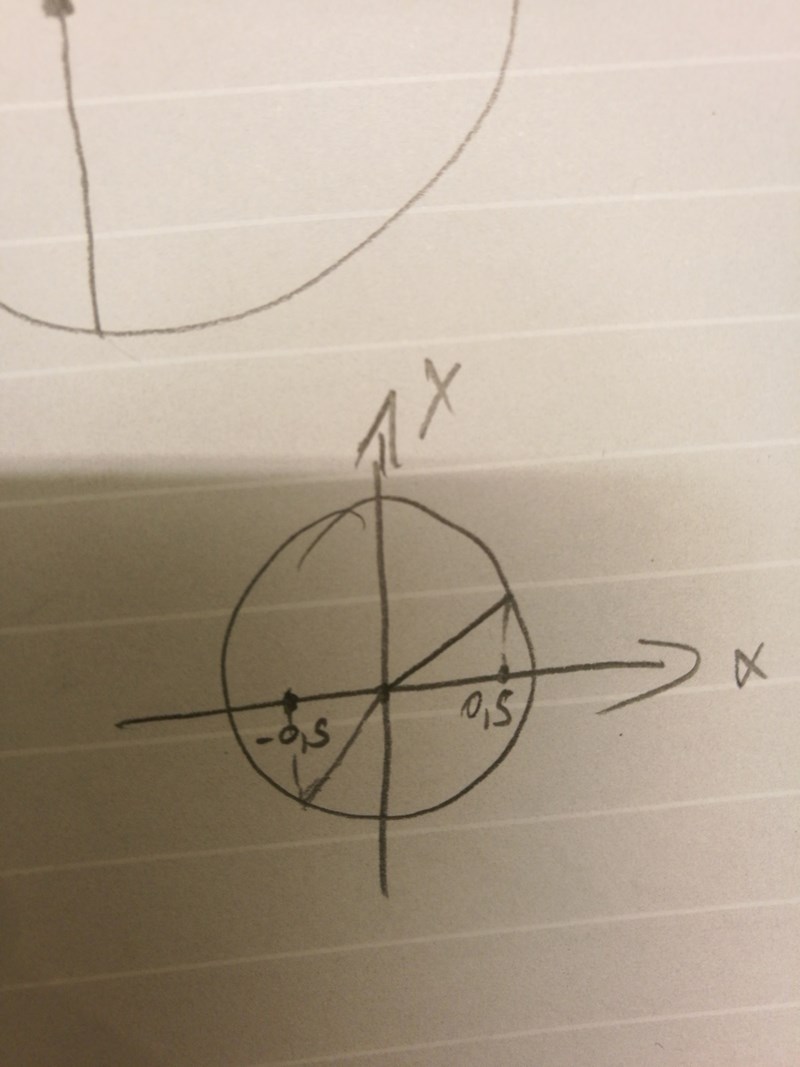
Nej nu ger jag upp och lägger upp en bild:
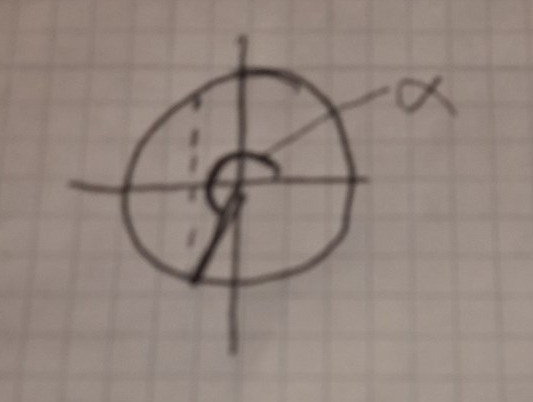
Smaragdalena skrev:Nej nu ger jag upp och lägger upp en bild:
Jaha okej du börjar på x= 0,5? Och går tills du kommer till 0,2?
Nej, jag börjar på v = 0 och fortsätter tills jag hamnar på rätt vinkel.
I vilken kvadrant hamnar vinkeln ?
Smaragdalena skrev:Nej, jag börjar på v = 0 och fortsätter tills jag hamnar på rätt vinkel.
I vilken kvadrant hamnar vinkeln ?
Första kvadranten 0-90 grader
Andra kvadranten 90-180 grader
Tredje kvadranten 180-270 grader
Fjärde kvadranten 270-360 grader
Så 360 grader är fjärde kvadranten
Ja, men i vilken kvadrant hamnar vinkeln ? Du ser att vinkeln är lite mer än halvvägs genom tredje kvadranten.
Smaragdalena skrev:Ja, men i vilken kvadrant hamnar vinkeln ? Du ser att vinkeln är lite mer än halvvägs genom tredje kvadranten.
Aa den hamnar i tredje kvadranten dvs denna vi räknade ut, alltså alltså sinalfa
Nej. Jag frågar inte efter vinkeln alfa, utan den vinkel som är precis dubbelt så stor, alltså TVÅalfa.
Smaragdalena skrev:Nej. Jag frågar inte efter vinkeln alfa, utan den vinkel som är precis dubbelt så stor, alltså TVÅalfa.
Då måste den väl ligga i fjärde kvadranten? Vad har vinkeln alfa och 2alfa gemensamt?
Nej. Rita en enhetscirkel och markera vinkeln som jag gjorde. Rita en vinkel till, lika stor sen vinkeln , som startar där den första vinkeln slutar. Lägg upp bilden här.
Smaragdalena skrev:
Nej. Rita en enhetscirkel och markera vinkeln som jag gjorde. Rita en vinkel till, lika stor sen vinkeln , som startar där den första vinkeln slutar. Lägg upp bilden här.
Den gröna är alfa och den svarta är 2alfa
Den svarta vinkeln och den gröna vinkeln är väl precis lika stora?
Smaragdalena skrev:Den svarta vinkeln och den gröna vinkeln är väl precis lika stora?
Aa de har samma värde
Jag tänkte om den istället kan se ut sådär? Men det ser ut som att vi har gått 360 grader åt andra hållet 
Vinkeln skall starta på positiva x-axeln, gå drygt ½ varv till och så lika långt till. Det blir sammanlagt lite drygt 5/4 varv. Vilken kvadrant hamnar man i då?
Smaragdalena skrev:
Vinkeln skall starta på positiva x-axeln, gå drygt ½ varv till och så lika långt till. Det blir sammanlagt lite drygt 5/4 varv. Vilken kvadrant hamnar man i då?
1 kvadranten
Nej, det skulle det ha varit om vinkeln var lite mindre, men om man ritat tydligt kan man se att vinkeln är större än så det blir lite förbi y-axeln.
Smaragdalena skrev:
Nej, det skulle det ha varit om vinkeln var lite mindre, men om man ritat tydligt kan man se att vinkeln är större än så det blir lite förbi y-axeln.
Det stämmer, men för en annan mycket mindre vinkel än alfa.
Hur stor är vinkeln alfa mätt i grader?
Smaragdalena skrev:Det stämmer, men för en annan mycket mindre vinkel än alfa.
Hur stor är vinkeln alfa mätt i grader?
Hm det vet jag ej eller jag känner mig trött i huvudet justnu för att tänka
Om vi säger att 2alfa är 540 grader så är alfa 270. Men vad exakt cosalfa=-1/5 är i grader utan miniräknare vet jag ej..
Det är en väldigt lång tråd, så jag kör en snabbrepetition av hur man börjar med uppgiften.
Cosinus för alfa är -1/5, så vi tittar på den här linjen i enhetscirkeln
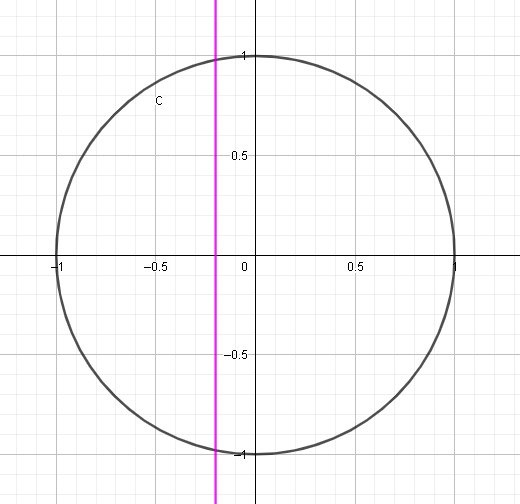
och då hittar vi två vinklar som har det värdet på cosinus
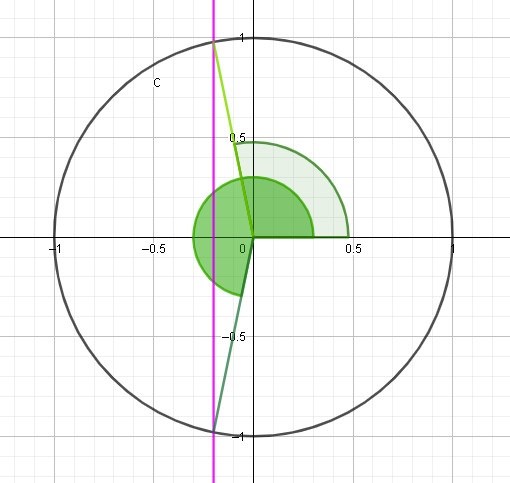
betyder att vinkeln vi är ute efter är mer än ett halvt varv, men mindre än ett helt varv.
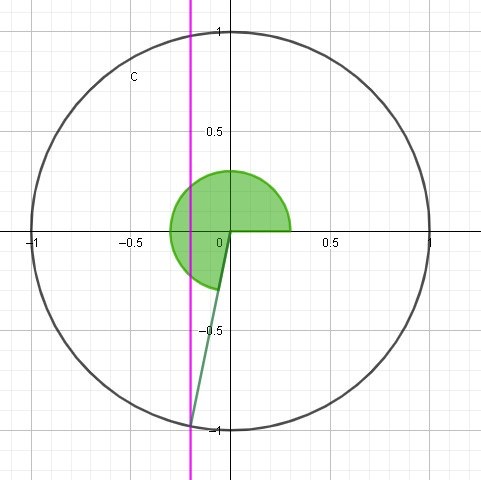
Bubo skrev:Det är en väldigt lång tråd, så jag kör en snabbrepetition av hur man börjar med uppgiften.
Cosinus för alfa är -1/5, så vi tittar på den här linjen i enhetscirkeln
och då hittar vi två vinklar som har det värdet på cosinus
betyder att vinkeln vi är ute efter är mer än ett halvt varv, men mindre än ett helt varv.
Markera vinklarna som du säger ger värdet cosalfa=-1/5