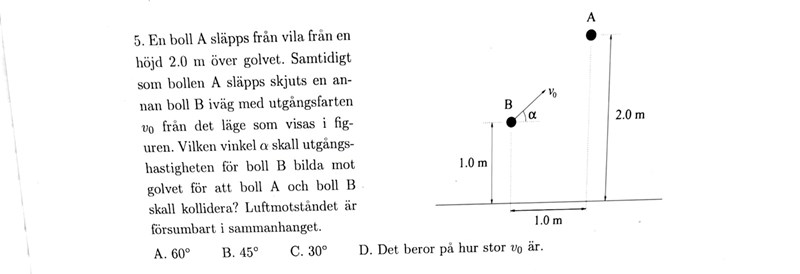
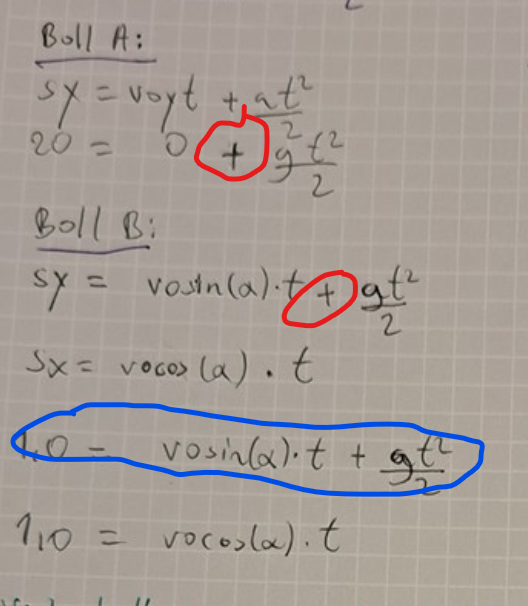MaFy 2009 uppgift 5
 Hej!
Hej!
Kan någon knuffa mig i rätt riktning? Jag är lite fast på denna fråga. Jag är dessutom osäker på om hastighet i y-led och x-led verkar under kollision samtidigt eller om en av dem gör det? Hur blir det med positiv riktning uppåt? Tacksam för hjälp!!
Vad menar du med "verkar under kollision samtidigt"?
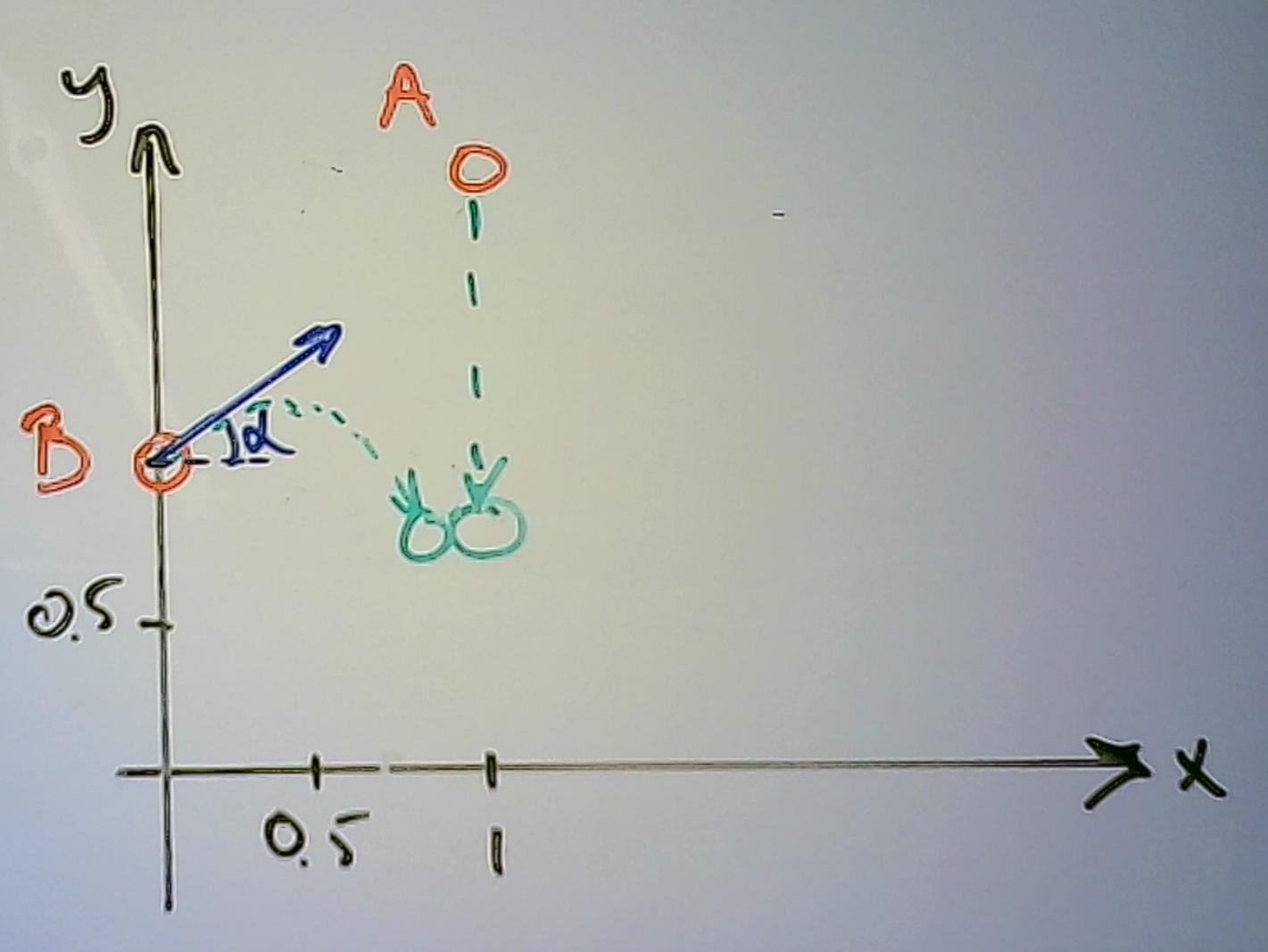
Jag skulle rita in situationen i ett koordinatsystem, för att göra det lite lättare att hålla ordning på riktningarna
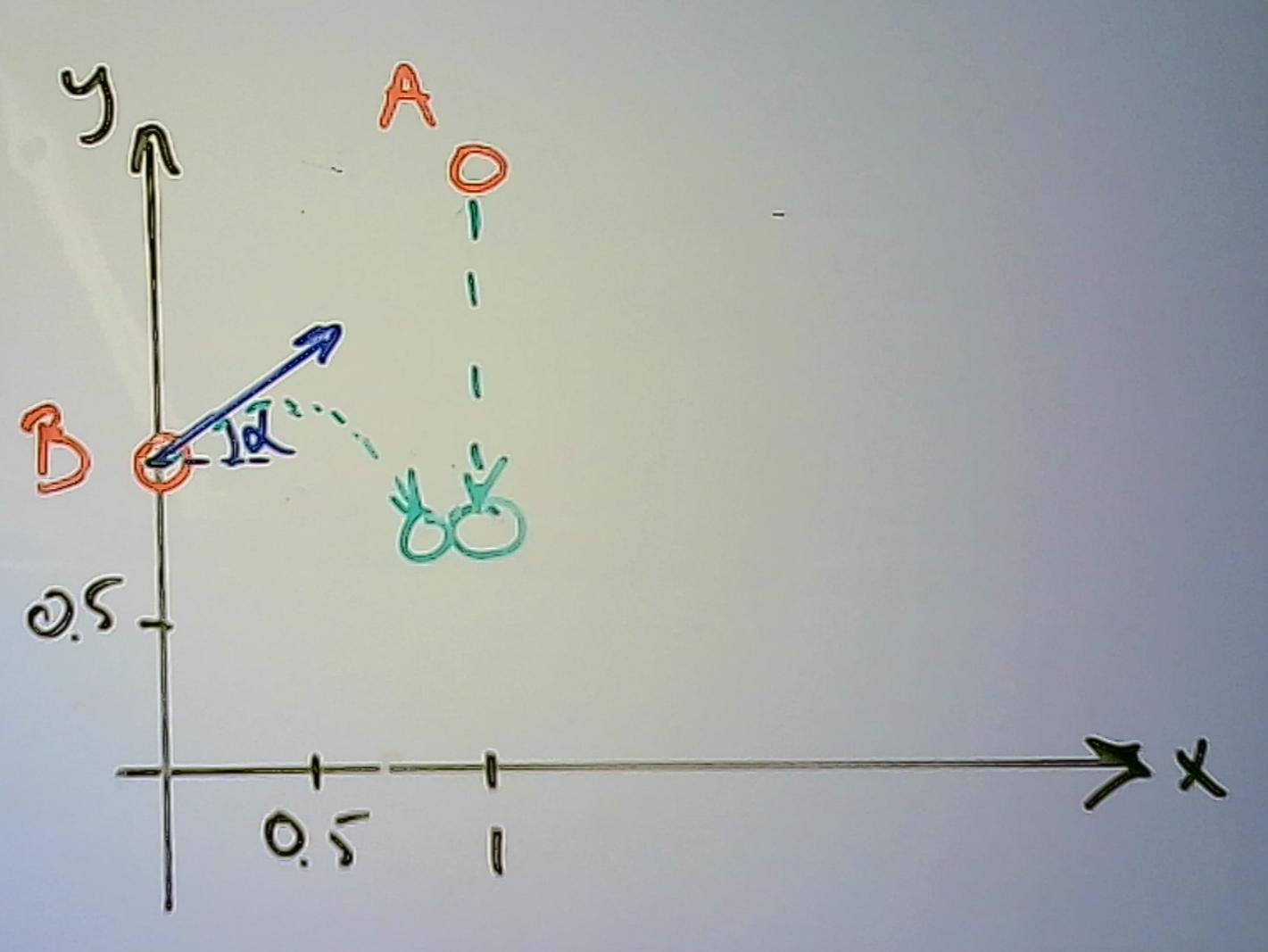
Eftersom positiv riktning är uppåt måste accelerationen vara negativ (tyngdkraften verkar nedåt)
I mitt koordinatsystem gäller för kula A
Ay = 2-gt2/2
Ax = 1
För Kula B gäller
By =
Bx =
När dom kolliderar är läget detsamma (och tiden ) så Ay = By och Ax = Bx
Ture skrev:Jag skulle rita in situationen i ett koordinatsystem, för att göra det lite lättare att hålla ordning på riktningarna
Eftersom positiv riktning är uppåt måste accelerationen vara negativ (tyngdkraften verkar nedåt)
I mitt koordinatsystem gäller för kula A
Ay = 2-gt2/2
Ax = 1
För Kula B gäller
By =
Bx =
När dom kolliderar är läget detsamma (och tiden ) så Ay = By och Ax = Bx
Jag förstår ej nu..
vad är det du inte förstår?
Ture skrev:vad är det du inte förstår?
Jag förstår ej dina ekvationer riktigt. Kan vi titta på mina ekvationer och lösa därifrån samt resonera därifrån,då blir det lättare att arbeta oss igenom
ok
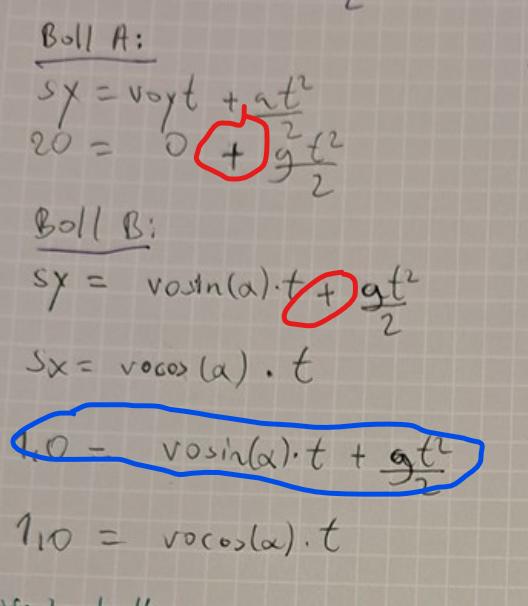
Där jag ringat in med rött ska det vara minustecken istället för plus eftersom accelerationen sker i negativ riktning
Den blå inringade ekvationen förstår jag inte vad den ska beskriva
På MaFy-uppgifter ska man inte ge sig in på att lösa kvadratiska ekvationer, det tar alldeles för lång tid.
Många av uppgifterna är flervalsfrågor och då brukar uteslutningsmetoden vara den snabbaste vägen.
I det här fallet kan man börja tänka på vilken riktning det ska vara om kula B har en mycket hög hastighet, så att tiden för träffen är liten (t ex mindre än en millisekund, eller nästan så nära noll som man vill ha den).
Jo det är förvisso sant, dock tror jag att det kan vara svårt för många att avgöra om B eller D är rätt alternativ.
Ture skrev:Jo det är förvisso sant, dock tror jag att det kan vara svårt för många att avgöra om B eller D är rätt alternativ.
Ja, det är nästa steg i resonemanget, och det är lite svarare att tänka helt säkert, men intuition hjälper nog att få bättre chans än 50 % att få det rätt.
Och redan 50 % är mycket bättre än att slösa för mycket tid på en av uppgifterna.
Ture skrev:ok
Där jag ringat in med rött ska det vara minustecken istället för plus eftersom accelerationen sker i negativ riktning
Den blå inringade ekvationen förstår jag inte vad den ska beskriva
Aa juste det är sant! Aa den blå ringade ekvationen försöker jag säga att Boll B har en hastighet i y-led med höjden 1.0 m. Men jag är osäker på om boll B har en utgångshöjd som de givit oss i frågan eller om den höjden betecknar höjden som den har när den faller ned.
Pieter Kuiper skrev:Ture skrev:Jo det är förvisso sant, dock tror jag att det kan vara svårt för många att avgöra om B eller D är rätt alternativ.
Ja, det är nästa steg i resonemanget, och det är lite svarare att tänka helt säkert, men intuition hjälper nog att få bättre chans än 50 % att få det rätt.
Och redan 50 % är mycket bättre än att slösa för mycket tid på en av uppgifterna.
det är vi helt eniga om,
Samtidigt är det bra träning för de studenter som är osäkra på kaströrelser att faktiskt lösa den här typen av uppgifter den tunga vägen, i alla fall på hemmaplan.
destiny99 skrev:Aa juste det är sant! Aa den blå ringade ekvationen försöker jag säga att Boll B har en hastighet i y-led med höjden 1.0 m.
Är det verkligen genomtänkt?
När bollarna träffar varandra, har de samma position
Så bestäm när dom har samma position i x-led dvs vid vilket t deras resp x koordinat är lika.
skapa sen ett uttryck för deras resp position i y-led för det värde på t du just räknat ut. Vad ska gälla för att dom ska vara lika?
Ture skrev:destiny99 skrev:Aa juste det är sant! Aa den blå ringade ekvationen försöker jag säga att Boll B har en hastighet i y-led med höjden 1.0 m.
Är det verkligen genomtänkt?
När bollarna träffar varandra, har de samma position
Så bestäm när dom har samma position i x-led dvs vid vilket t deras resp x koordinat är lika.
skapa sen ett uttryck för deras resp position i y-led för det värde på t du just räknat ut. Vad ska gälla för att dom ska vara lika?
Grejen är såhär att jag bara skrev hur läget är för Boll B enbart innan krock tillståndet (det blåa inrigade ekvationen) för att skaffa mig en uppfattning först. Men ska jag radera den ekvationen ?
Ja, den ger ingenting, prova istället att göra som jag föreslog i #13
Ture skrev:Ja, den ger ingenting, prova istället att göra som jag föreslog i #13
Yes jag provade att göra koordinatsystem där vi utgår från B:s koordinatsystem så fick jag det till såhär. Då blev alfa 45 grader. Det tog ett tag att greppa detta men nu har man förstått detta!

det är bra,
några formell fel hittar jag här och där, se nedan

Ture skrev:det är bra,
några formell fel hittar jag här och där, se nedan
Varför är dessa fel?
Korrigering
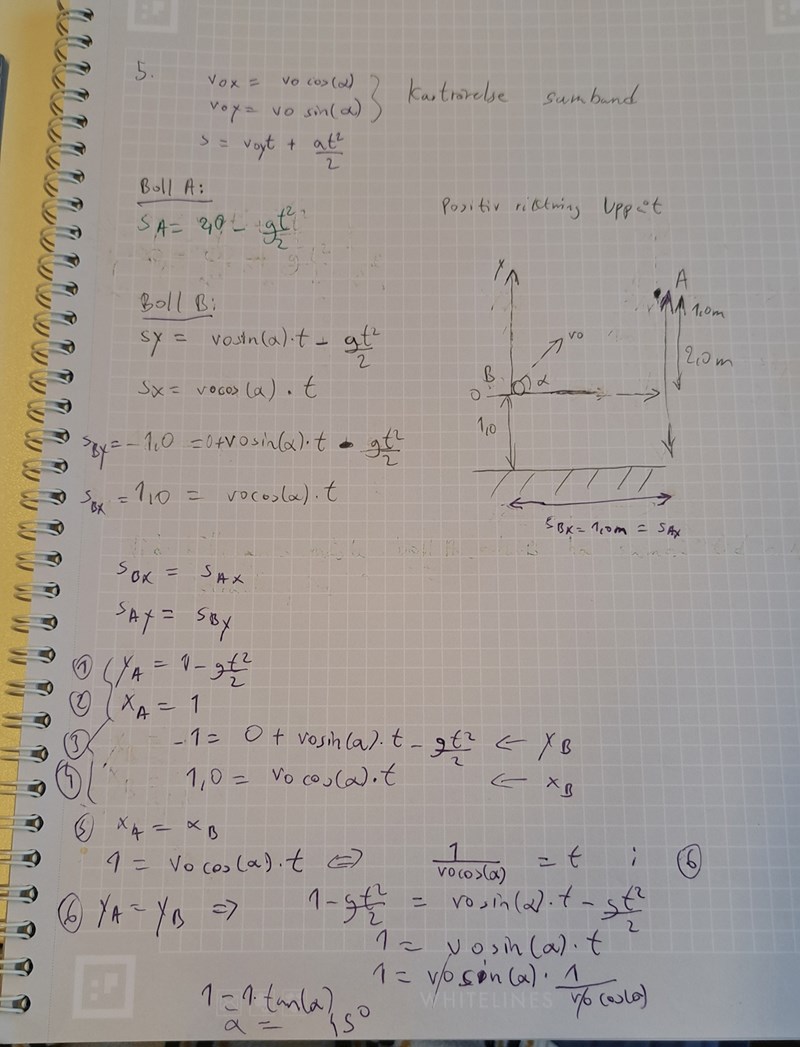
ta det här som exempel,
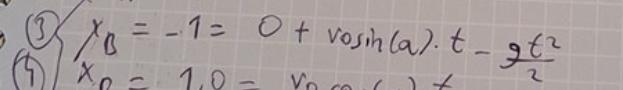
Du har definierat origo i ditt koordinatsystem som platsen där kula B ligger i startögonblicket.
sen skriver du enl ovan,: yB = -1 = 0+v0... osv
Vad gör -1 där ? Det betyder att yB alltid = -1 ! och så är det ju inte.
Det ska stå ett uttryck som i varje ögonblick beskriver boll Bs y koordinat i ditt koordinatsystem
dvs
yB = 0 + v0sin(... osv
Ture skrev:ta det här som exempel,
Du har definierat origo i ditt koordinatsystem som platsen där kula B ligger i startögonblicket.
sen skriver du enl ovan,: yB = -1 = 0+v0... osv
Vad gör -1 där ? Det betyder att yB alltid = -1 ! och så är det ju inte.
Det ska stå ett uttryck som i varje ögonblick beskriver boll Bs y koordinat i ditt koordinatsystem
dvs
yB = 0 + v0sin(... osv
Asså om jag sätter kordinatsystem där B ligger så kommer boll B kastas med y0=0 och och då är yb=-1 på grund av att höjden är under origo och positiv riktning är vald uppåt. Jag vet ej hur man ska skriva det på sättet som det förväntas. Jag misstänker det är skillnad på yb och y0(starthöjden)
Därför har vi
yb=0+v0sin(a)-gt^2/2 där yb=-1. Starthöjden här är 0 eftersom vi börjar på origo i B:s startögonblick.
destiny99 skrev:Asså om jag sätter kordinatsystem där B ligger så kommer boll B kastas med y0=0 och och då är yb=-1 på grund av att höjden är under origo och positiv riktning är vald uppåt. Jag vet ej hur man ska skriva det på sättet som det förväntas. Jag misstänker det är skillnad på yb och y0(starthöjden)
Därför har vi
yb=0+v0sin(a)-gt^2/2 där yb=-1. Starthöjden här är 0 eftersom vi börjar på origo i B:s startögonblick.
yB är boll Bs y koordinat i det koordinatsystem som har boll Bs startpunkt som origo, dvs precis som du ritade i #16
Alltså
Det här är rätt:
yb=0+v0t*sin(a)-gt^2/2
yb vid t = 0 är 0
Det här är fel:
yb=-1
yb = -1 gäller vid ett visst ögonblick, men vi är överhuvudtaget inte intresserade av det!
Ture skrev:destiny99 skrev:Asså om jag sätter kordinatsystem där B ligger så kommer boll B kastas med y0=0 och och då är yb=-1 på grund av att höjden är under origo och positiv riktning är vald uppåt. Jag vet ej hur man ska skriva det på sättet som det förväntas. Jag misstänker det är skillnad på yb och y0(starthöjden)
Därför har vi
yb=0+v0sin(a)-gt^2/2 där yb=-1. Starthöjden här är 0 eftersom vi börjar på origo i B:s startögonblick.
yB är boll Bs y koordinat i det koordinatsystem som har boll Bs startpunkt som origo, dvs precis som du ritade i #16
Alltså
Det här är rätt:
yb=0+v0t*sin(a)-gt^2/2
yb vid t = 0 är 0
Det här är fel:
yb=-1
yb = -1 gäller vid ett visst ögonblick, men vi är överhuvudtaget inte intresserade av det!
Men då blir ekvationen svårt att lösa när yA=yB
2-gt^2/2=v0sinalfa*t-gt^2/2
kvar har vi 2=v0sinalfa*t.
Men vi vet att xb=v0cosv*t då xb=1
1/v0sinalfa=t och sen har vi
2=tan(a)*1
destiny99 skrev:
Men då blir ekvationen svårt att lösa när yA=yB
2-gt^2/2=v0sinalfa*t-gt^2/2
VAr kom 2 ifrån?? i det koordinatsystem du definierat är startpositionen ya = 1
Ture skrev:destiny99 skrev:
Men då blir ekvationen svårt att lösa när yA=yB
2-gt^2/2=v0sinalfa*t-gt^2/2
VAr kom 2 ifrån?? i det koordinatsystem du definierat är startpositionen ya = 1
oj förlåt jag menar att yA=2-gt^2/2 . Ja men jag undrar om ej det är bättre att definiera startpositionen y_A=2 m dä uppgiften startade med 2 m för boll A. Jag vet ej varför jag införde y_A =1 m ,förmodligen för att göra beräkningarna enklare..
Tillägg: 9 mar 2024 16:23
Nu kom jag på att om jag sätter koordinatsystemet på marken och låter B kastas upp därifrån så kommer starthöjden att vara 1.0 m för Boll B och då blir det yb=1.0+v0sin(a)×t-gt^2/2.
(Kort inpass: jag tror att när man har formulerat färdigt rörelseekvationerna så kommer termerna som innehåller g att ta ut varandra, så att det som såg ut som andragradsekvationer blir linjära ekvationer. Men bryr er inte om det nu, om det låter obegripligt.)
Laguna skrev:(Kort inpass: jag tror att när man har formulerat färdigt rörelseekvationerna så kommer termerna som innehåller g att ta ut varandra, så att det som såg ut som andragradsekvationer blir linjära ekvationer. Men bryr er inte om det nu, om det låter obegripligt.)
Ja det är sant men hur löser vi vinkeln om vi bara har tan(a)=2? Det går väl ej om vi ej har tan(a)=1. Därför funkar det om vi sätter koordinatsystemet i marken och tänker som jag gjorde nu
Du kan sätta koordinatsystemet var som helst.
Men om du flyttar på det måste du se över samtliga ekvationer. Om du gör rätt blir det i slutändan exakt samma resultat.