MAFY 2016 Uppgift 12
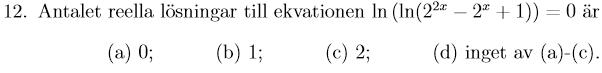
Jag fick svaret till a eftersom e upphöjt till något tal kan inte bli 0, vad har jag missat?
Svaret ska bli:
Visa spoiler
b
Det som du gör i ovanstående uträkning är att undersöka om x=0 är en lösning till ekvationen.
Det du kommer fram till är att så inte är fallet.
Detta säger bara att x=0 inte är en lösning; det säger ingenting om hur många andra eventuella lösningar som finns.
Det du bör göra att försöka förenkla uttrycket utan att sätta in ett värde på x.
Steg 1 borde vara att om
borde
och även
Applicera ovanstående resonemang två gånger för att bli av med de två logaritmerna.
redan från nästa fjärde sista raden kan man då konstatera att det finns endast en lösning
martinmaskin2 skrev:redan från nästa fjärde sista raden kan man då konstatera att det finns endast en lösning
Nu blir det dock fel:
Du kan ansätta att för att komma framåt.


