Jag förstår ej varför rätt svar ej är b). B stämmer ju ej men det gör a och d. det stämmer ju att dess diagnoler delar varandra mitt itu och bisektriser till varandra vid hörnen. Men jag vet ej hur de vill att man ska tänka
Du måste tänka "finns det någon annan sorts fyrhörning än en romb som påståendet också stämmer för?". Ta till exempel en rektangel med olika långa sidor. Dess diagonaler delar också varandra mitt itu, men den är ingen romb.
Och vad menar du med att b inte stämmer? Kan du rita en romb där diagonalerna inte bildar rät vinkel?
SvanteR skrev:Du måste tänka "finns det någon annan sorts fyrhörning än en romb som påståendet också stämmer för?". Ta till exempel en rektangel med olika långa sidor. Dess diagonaler delar också varandra mitt itu, men den är ingen romb.
Och vad menar du med att b inte stämmer? Kan du rita en romb där diagonalerna inte bildar rät vinkel?
Ja om vi ritar en rektangel. Då delar de varandra mitt itu, alltså diagnolerna men diagnolerna bildar ej rät vinkel som de gör med romb. En annan sak är att diagnolerna för en rektangel är bisektriser till vinklar i närheten. Sen har vi kvadrat som också är en typ av romb och det är samma som en rektangel. En kvadrat är också en fyrhörning?
Nja, du behöver nog kolla upp skillanderna mellan olika typer av fyrhörningar lite. Du skriver "att diagnolerna för en rektangel är bisektriser till vinklar i närheten" men det stämmer inte!
Ta ett rutat papper och rita en rektangel där ena sidan är en ruta och andra sidan är tio rutor. Rita in diagonalerna och titta på vinklarna. Om diagonalen är en bisektris så ska den dela den räta vinkeln i hörnet i två lika stora vinklar. Gör den det om du ritar?
SvanteR skrev:Nja, du behöver nog kolla upp skillanderna mellan olika typer av fyrhörningar lite. Du skriver "att diagnolerna för en rektangel är bisektriser till vinklar i närheten" men det stämmer inte!
Ta ett rutat papper och rita en rektangel där ena sidan är en ruta och andra sidan är tio rutor. Rita in diagonalerna och titta på vinklarna. Om diagonalen är en bisektris så ska den dela den räta vinkeln i hörnet i två lika stora vinklar. Gör den det om du ritar?
Hm jag tror ej jag förstår hur du vill att jag ska rita dem. Jag får nog ta upp frågan på en räknestuga istället. Så blir det klarare.
Här är en rektangel med diagonaler. Jag har markerat två vinklar. Är de lika stora? (Om diagonalen är en bisektris skulle de vara lika stora)
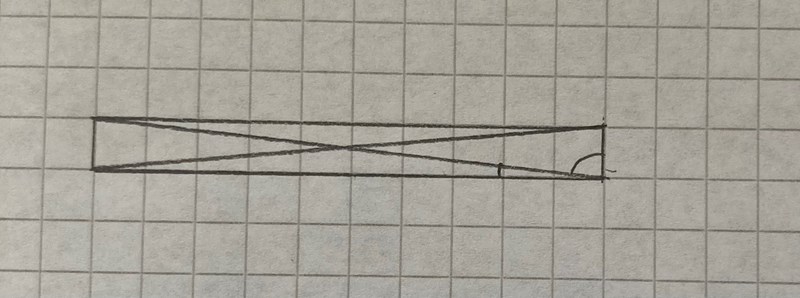
SvanteR skrev:Här är en rektangel med diagonaler. Jag har markerat två vinklar. Är de lika stora? (Om diagonalen är en bisektris skulle de vara lika stora)
Jag förstår ej din figur. Försöker du säga att det är omöjligt att en rektangels diagnolen kan dela bisektris?
Det verkar ej som att vinklarna är lika stora i din figur. Men tror du uppgiften är ute efter en rektangel eller en kvadrat?
Jag förstår inte riktigt din fråga. Uppgiften handlar ju om en romb!
SvanteR skrev:Jag förstår inte riktigt din fråga. Uppgiften handlar ju om en romb!
De säger en fyrhörning är en romb. Inte romb som man vet normalt. När blev en fyrhörning en romb? a, b och c alternativ handlar om romb. Det stämmer in på det. Men facit väljer alternativ c. Varför gör de det? Det är det jag ej förstår. De stryker bort alla andra och väljer c.
De frågar efter vad som är ett tillräckligt villkor för att en fyrhörning ska vara en romb.
(a) och (b) gäller alltid för romber men också för en del fyrhörningar som inte är romber.
Bara (c) gäller för alla romber och bara för romber.
Är (c) uppfyllt vet man att det är en romb.
Louis skrev:De frågar efter vad som är ett tillräckligt villkor för att en fyrhörning ska vara en romb.
(a) och (b) gäller alltid för romber men också för en del fyrhörningar som inte är romber.
Bara (c) gäller för alla romber och bara för romber.
Är (c) uppfyllt vet man att det är en romb.
Så om jag förstod frågan rätt så vill man veta specifikt vad som skiljer romb från andra geometriska figurer, alltså egenskaperna? Så om du tex har en kvadrat som både är en fyrhörning och har diagnoler som delar varandra mitt itu så menar du att diagnolerna till kvadraten ej kan vara besiktriser?
En kvadrat är en romb.
Mahiya99 skrev:SvanteR skrev:Jag förstår inte riktigt din fråga. Uppgiften handlar ju om en romb!
De säger en fyrhörning är en romb. Inte romb som man vet normalt. När blev en fyrhörning en romb? a, b och c alternativ handlar om romb. Det stämmer in på det. Men facit väljer alternativ c. Varför gör de det? Det är det jag ej förstår. De stryker bort alla andra och väljer c.
Nej, de säger inte att en fyrhörning är en romb. Orden "givet att" betyder i det är sammanhanget "om". Frågan går alltså ut på att du ska välja mellan alternativen:
(a) En fyrhörning är en romb om dess diagonaler delar varandra mitt itu.
(b) En fyrhörning är en romb om dess diagonaler bildar rät vinkel.
(c) En fyrhörning är en romb om dess diagonaler är bisektriser till vinklarna i hörnen.
Men nu när jag tänker igenom frågan ordentligt måste jag erkänna att jag har svarat slarvigt tidigare i tråden. b är fel svar, men inte för att det inte stämmer utan för att det går att rita (oregelbundna) fyrhörningar där diagonalerna bildar en rät vinkel. b är alltså sant för romber men även för andra fyrhörningar.
SvanteR skrev:Mahiya99 skrev:SvanteR skrev:Jag förstår inte riktigt din fråga. Uppgiften handlar ju om en romb!
De säger en fyrhörning är en romb. Inte romb som man vet normalt. När blev en fyrhörning en romb? a, b och c alternativ handlar om romb. Det stämmer in på det. Men facit väljer alternativ c. Varför gör de det? Det är det jag ej förstår. De stryker bort alla andra och väljer c.
Nej, de säger inte att en fyrhörning är en romb. Orden "givet att" betyder i det är sammanhanget "om". Frågan går alltså ut på att du ska välja mellan alternativen:
(a) En fyrhörning är en romb om dess diagonaler delar varandra mitt itu.
(b) En fyrhörning är en romb om dess diagonaler bildar rät vinkel.
(c) En fyrhörning är en romb om dess diagonaler är bisektriser till vinklarna i hörnen.
Men nu när jag tänker igenom frågan ordentligt måste jag erkänna att jag har svarat slarvigt tidigare i tråden. b är fel svar, men inte för att det inte stämmer utan för att det går att rita (oregelbundna) fyrhörningar där diagonalerna bildar en rät vinkel. b är alltså sant för romber men även för andra fyrhörningar.
Aa jag är fortfarande ej med på varför c är rätt svar. Det är sant a), b) och c) gäller för romber. Men vilka andra fyrhörningar frågan pratar om vet jag ej, det enda fyrhörning jag kommer på är en rektangel.
Frågan är vilket villkor som bara gäller för romber.
Och därför, om det är uppfyllt, säger det här är en romb.
Det gör inte (a) eller (b).
Det här är ju en romb?
a gäller för rektanglar också, så det kan inte vara rätt svar.
b gäller för en massa oregelbundna fyrhörningar, så det är inte rätt svar. Kolla på bilden:
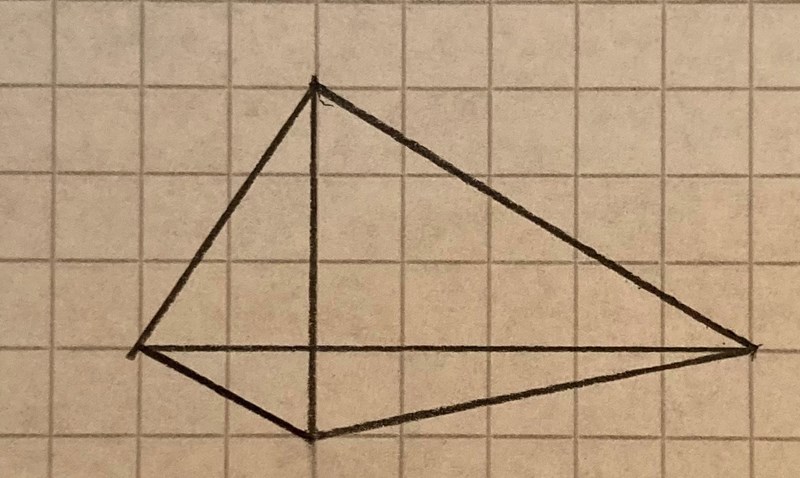
SvanteR skrev:a gäller för rektanglar också, så det kan inte vara rätt svar.
b gäller för en massa oregelbundna fyrhörningar, så det är inte rätt svar. Kolla på bilden:
Ja a) och b) stämmer för denna romb.


