Mafy 2021 Fråga 18
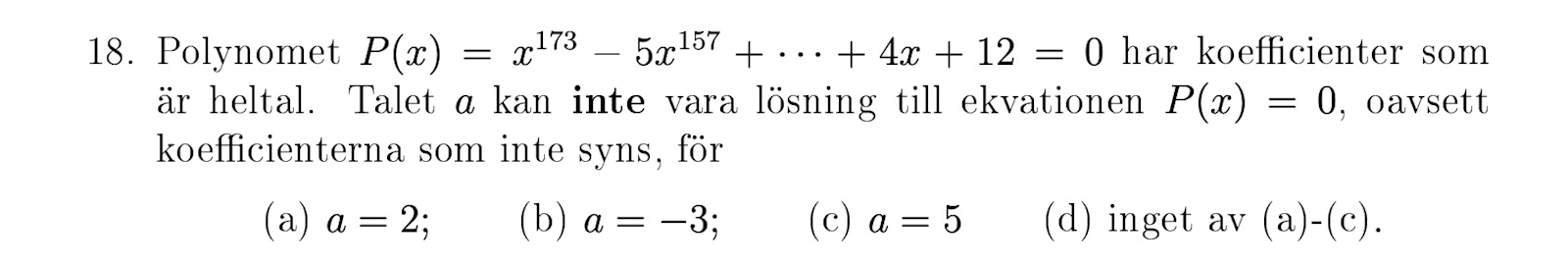 Enligt chatgpt måste roten dela konstanttermen 12 ifall det ska vara en rot. (Om alla riktingskoefficienter är heltal) Det framkommer inte ens i uppgiften att alla koefficienter är heltal. Men men..
Enligt chatgpt måste roten dela konstanttermen 12 ifall det ska vara en rot. (Om alla riktingskoefficienter är heltal) Det framkommer inte ens i uppgiften att alla koefficienter är heltal. Men men..
Har ni andra funderingar på hur man kan lösa den ?
Det framkommer inte ens i uppgiften att alla koefficienter är heltal.
Det står visst i uppgiften.
"Polynomet P(x) [...] har koefficienter som är heltal"
Om vi stoppar in talet 5 i polynomet kommer alla termer som innehåller ett , alltså alla termer förutom det sista, vara delbara med 5. Eftersom det sista talet inte är delbart med 5 innebär det att inte är delbar med 5. Eftersom 0 är delbar med 5 kan inte vara lika med 0. (Egentligen samma argument som att konstatera att 5 inte delar 12)
AlexMu skrev:Det framkommer inte ens i uppgiften att alla koefficienter är heltal.
Det står visst i uppgiften.
"Polynomet P(x) [...] har koefficienter som är heltal"
Om vi stoppar in talet 5 i polynomet kommer alla termer som innehåller ett , alltså alla termer förutom det sista, vara delbara med 5. Eftersom det sista talet inte är delbart med 5 innebär det att inte är delbar med 5. Eftersom 0 är delbar med 5 kan inte vara lika med 0. (Egentligen samma argument som att konstatera att 5 inte delar 12)
Jag skrev: "Det framkomer inte att alla koefficienter är heltal"
Förstår inte varför a är en rot ifall det är delbart med konstanttermen? Och om 12 inte är delbart med 5? Det känns rörigt, att alla olika 170+ termer om det är så många att dem kanske ändå gör att det blir 0 på något sätt. Hänger ej med
I alla termer förutom den sista finns ett .
Vi kan då skriva som
Insättning ger att
där är något heltal.
Finns det några heltalslösningar för till ekvationen ?
Vilken otroligt bra förklaring, ska smälta det mer senare. Återkommer, mycket imponerande. Bra jobbat
Korra skrev:Vilken otroligt bra förklaring, ska smälta det mer senare. Återkommer, mycket imponerande. Bra jobbat
Tack! Fyi: Detta kan generaliseras lite mer till något som kallas för "Rational root theorem".
Den säger att om ett polynom med heltalskoefficienter har en rationell rot . Alltså att
med heltal och som är förkortade så långt som möjligt (de delar inga faktorer)
Så gäller det att konstanttermen är delbar med och koefficienten framför termen med högst exponent är delbar med .
Exempel:
Om gäller det att alltså att är delbar med och är delbar med . Då finns det inte många värden på och .
kan vara och kan vara , eller
Vilket ger alla möjliga kandidater på rationella rötter:
, , , , ,
I detta fall tror jag den enda rationella roten är (Då kan man faktorisera pga faktorsatsen och hitta de andra två (irrationella) med pq!).
Trevlig sats om man vill hitta alla rötter till ett polynom av högre gradtal än 2 algebraiskt
Fallet ovan från MaFy kan vi då tänka oss ett specialfall där .


