MAFY 2021 Uppgift 22
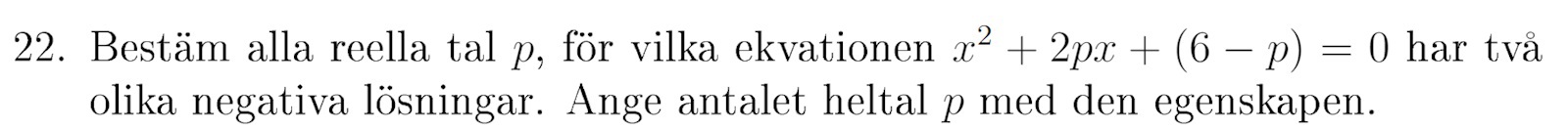
När jag löser så får jag att p6. I facit står det att svaret är 3. Kan jag få en ledtråd på hur jag ska gå tillväga eller var jag hade gjort fel:
Du tänker rätt! :)
För att vi ska ha två olika lösningar överhuvudtaget måste diskriminanten vara positiv, alltså
Därefter tillkommer vad som händer med vårt rotuttryck. Både och måste vara negativa, men eftersom rotuttrycket i sig alltid är positivt, kan vi fokusera enbart på det första alternativet. Vi vill alltså att
Vilka p uppfyller detta? :)
Smutstvätt skrev:Du tänker rätt! :)
För att vi ska ha två olika lösningar överhuvudtaget måste diskriminanten vara positiv, alltså
Därefter tillkommer vad som händer med vårt rotuttryck. Både och måste vara negativa, men eftersom rotuttrycket i sig alltid är positivt, kan vi fokusera enbart på det första alternativet. Vi vill alltså att
Vilka p uppfyller detta? :)
Jag tror att olikhetsteckena ska vara omvända på de två sista raderna du har skrivit. Jag har dessutom kommit fram till att
p6
Kan inte tänka på ett annat sätt så att lösningen blir en tria istället för en sexa
Nu har jag kollat genom uppgiften ordentligt. i början visade du att i och med att diskriminanten är positiv så ska p antigen vara större än två eller mindre än -3. Löser jag ut det sista ekcationen får jag att p ska vara mindre än 6. Antalet heltal p blir då p = 3, p = 4 och p = 5. Alltså 3 st. Men borde vi inte ha fler lösningar med tanke på att p kan också vara mindre än -3 ?
Jag tror att olikhetsteckena ska vara omvända på de två sista raderna du har skrivit. Jag har dessutom kommit fram till att
p<6
Kan inte tänka på ett annat sätt så att lösningen blir en tria istället för en sexa
Ursäkta, det har du helt rätt i. Jag har ändrat, tack för dina skarpa ögon!
Nu har jag kollat genom uppgiften ordentligt. i början visade du att i och med att diskriminanten är positiv så ska p antigen vara större än två eller mindre än -3. Löser jag ut det sista ekcationen får jag att p ska vara mindre än 6. Antalet heltal p blir då p = 3, p = 4 och p = 5. Alltså 3 st. Men borde vi inte ha fler lösningar med tanke på att p kan också vara mindre än -3 ?
3, 4 och 5 stämmer. Vad det gäller , så nja. Eftersom , innebär det att om p är negativt, måste även rotuttrycket vara negativt, vilket inte är tillåtet. :)
Smutstvätt skrev:Jag tror att olikhetsteckena ska vara omvända på de två sista raderna du har skrivit. Jag har dessutom kommit fram till att
p<6
Kan inte tänka på ett annat sätt så att lösningen blir en tria istället för en sexa
Ursäkta, det har du helt rätt i. Jag har ändrat, tack för dina skarpa ögon!
Nu har jag kollat genom uppgiften ordentligt. i början visade du att i och med att diskriminanten är positiv så ska p antigen vara större än två eller mindre än -3. Löser jag ut det sista ekcationen får jag att p ska vara mindre än 6. Antalet heltal p blir då p = 3, p = 4 och p = 5. Alltså 3 st. Men borde vi inte ha fler lösningar med tanke på att p kan också vara mindre än -3 ?
3, 4 och 5 stämmer. Vad det gäller , så nja. Eftersom , innebär det att om p är negativt, måste även rotuttrycket vara negativt, vilket inte är tillåtet. :)
Tackar, tackar!!



