MAFY 2021 Uppgift 27
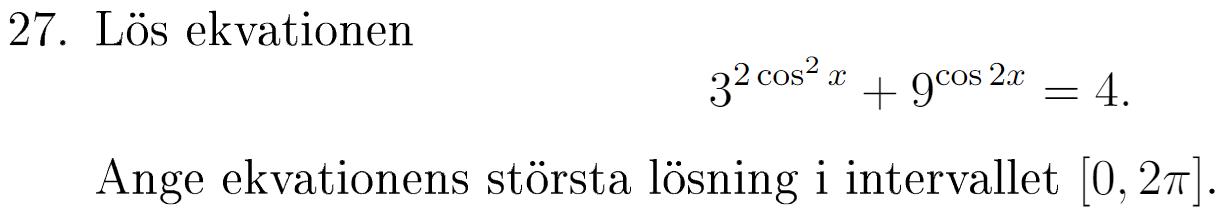
Kan någon ge mig en ledtråd på hur jag borde tänka? Svaret ska bli
Börja med
cos(2x)=2cos^2(x)-1
Nedan förkortar jag cos(x) med c
Ekvationen kan då skrivas
3^(2c^2) + 9^(2c^2-1) = 4
(3^2)^(c^2) + 9^(2c^2)/9 = 4
9^(c^2) + (9^(c^2))^2/9 = 4
Sätt t=9^(c^2) varpå ekvationen övergår i
t + t^2/9 = 4
som har lösningarna t=-12 och t=3.
Den negativa lösningen förkastas då t>0
Alltså har vi att 9^(c^2) = 3 vilket ger att c^2 = 1/2 varför c=±1/sqrt(2)
Då c = cos(x) har vi nu
cos(x) = ±1/sqrt(2)
vilket har kända lösningar och du får ditt svar genom att betrakta de fyra lösningarna och välja den största i givet intervall.
Trinity2 skrev:Börja med
cos(2x)=2cos^2(x)-1
Nedan förkortar jag cos(x) med c
Ekvationen kan då skrivas
3^(2c^2) + 9^(2c^2-1) = 4
(3^2)^(c^2) + 9^(2c^2)/9 = 4
9^(c^2) + (9^(c^2))^2/9 = 4
Sätt t=9^(c^2) varpå ekvationen övergår i
t + t^2/9 = 4
som har lösningarna t=-12 och t=3.
Den negativa lösningen förkastas då t>0
Alltså har vi att 9^(c^2) = 3 vilket ger att c^2 = 1/2 varför c=±1/sqrt(2)
Då c = cos(x) har vi nu
cos(x) = ±1/sqrt(2)
vilket har kända lösningar och du får ditt svar genom att betrakta de fyra lösningarna och välja den största i givet intervall.
Yes! När jag löser det så får jag att x är antigen eller .
Tack så mycket för hjälpen!
Hassan1 skrev:Yes! När jag löser det så får jag att x är antigen eller .
Fundera på hur det kommer sig att du tappar hälften av lösningarna.


