Mafy 2022 Uppgift 22

Pröva följande metod:

För att ekvationen ska ha två olika lösningar måste $p\neq0$.

Skriv därför om ekvationen på formen $x^2+\frac{1+p^2}{p}x+1=0$

Använd att sambanden mellan rötter $x_1$, $x_2$ och koefficienter $b$ och $c$ i ekvationen $x^2+bx+c=0$ är 

• $x_1\cdot x_2=c$, dvs $x_1\cdot x_2=1$
• $x_1+x_2=-b$, dvs $x_1+x_2=-\frac{1+p^2}{p}$

Du vill även ha att $\frac{x_2}{x_1}=2$

Yngve skrev:

• $x_1+x_2=-b$, dvs $x_1+x_2=-\frac{1+p^2}{p}$

Varför -b? 

Dani163 skrev:

Varför -b? 

Lös ekvationen x²+bx+q=0 och summera x₁ och x₂ så ser du att det är så.

Yngve skrev:

Pröva följande metod:

För att ekvationen ska ha två olika lösningar måste $p\neq0$.

Skriv därför om ekvationen på formen $x^2+\frac{1+p^2}{p}x+1=0$

Använd att sambanden mellan rötter $x_1$, $x_2$ och koefficienter $b$ och $c$ i ekvationen $x^2+bx+c=0$ är 

• $x_1\cdot x_2=c$, dvs $x_1\cdot x_2=1$
• $x_1+x_2=-b$, dvs $x_1+x_2=-\frac{1+p^2}{p}$

Du vill även ha att $\frac{x_2}{x_1}=2$

Vi börjar med att skriva om ekvationen på standardform:

$p x^2+\left(1+p^2\right) x+p=0 \Rightarrow x^2 + \frac{1+p^2}{p}x + 1=0$

Enligt ledtråden vet vi att lösningarna till ekvationen uppfyller följande system av ekvationer:

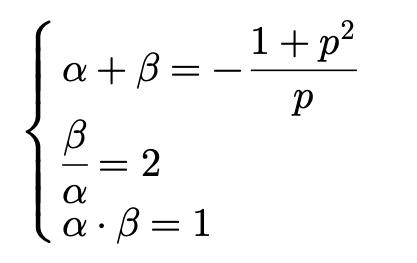
där $\alpha$ och $\beta$ är rötterna till ekvationen.

Vi kan använda den tredje ekvationen för att eliminera $\beta$ från de första två ekvationerna:

$\alpha \cdot \beta = 1 \\$

$\frac{\beta}{\alpha} = 2 \\$

$\Rightarrow 2\alpha = \beta \\$

Vi kan nu ersätta $\beta$:

$\alpha + \beta = -\frac{1+p^2}{p} \\$

$\Rightarrow \alpha + 2\alpha = -\frac{1+p^2}{p} \\$

$\Rightarrow 3\alpha = -\frac{1+p^2}{p} \\$

Fast här insåg jag att jag är ute och cyklar och inte vet vad jag håller på med. Kan någon hjälpa mig vidare härifrån?

Fast här insåg jag att jag är ute och cyklar och inte vet vad jag håller på med. Kan någon hjälpa mig vidare härhärifrån

Sambanden $\alpha\cdot\beta=1$ och $\beta=2\alpha$ ger dig att $\alpha\cdot2\alpha=1$, dvs $\alpha=\pm\frac{1}{\sqrt{2}}$

Yngve skrev:

Fast här insåg jag att jag är ute och cyklar och inte vet vad jag håller på med. Kan någon hjälpa mig vidare härhärifrån

Sambanden $\alpha\cdot\beta=1$ och $\beta=2\alpha$ ger dig att $\alpha\cdot2\alpha=1$, dvs $\alpha=\pm\frac{1}{\sqrt{2}}$

Efter att ha ersatt $\beta$ med $2\alpha$ i ekvationen $\alpha+\beta=-\frac{1+p^2}{p}$ får vi:

$\alpha+2\alpha=-\frac{1+p^2}{p}$

vilket ger oss:

$3\alpha=-\frac{1+p^2}{p}$

Nu kan vi lösa för $\alpha$ genom att multiplicera båda sidor med $\frac{p}{3}$:

$\alpha = -\frac{1+p^2}{3p}$

Sedan kan vi använda sambandet $\beta=2\alpha$ för att lösa för $\beta$:

$\beta=2\alpha=-\frac{2(1+p^2)}{3p}$

Nu kan vi använda den tredje ekvationen i systemet för att hitta kvoten mellan lösningarna:

$\frac{\beta}{\alpha}=\frac{-\frac{2(1+p^2)}{3p}}{-\frac{1+p^2}{3p}}=2$

Så vad säger detta oss, nu?

Du har inte använt det samband jag tipsade om i svar #6.

Vi backar tillbaka lite.

Vi vet att $\alpha=\pm\frac{1}{\sqrt{2}}$ och vi ser nu vilka motsvarande värden på $\beta$ vi då får:

• För $\alpha_1=\frac{1}{\sqrt{2}}$ får vi att $\beta_1=2\alpha_1=\frac{2}{\sqrt{2}}$.
• För $\alpha_2=-\frac{1}{\sqrt{2}}$ får vi att $\beta_2=2\alpha_2=-\frac{2}{\sqrt{2}}$.

Nu kan vi använda detta i sambandet $\alpha+\beta=-\frac{1+p^2}{p}$ Vilket ger oss följande två fall:

• Fall 1: $\frac{1}{\sqrt{2}}+\frac{2}{\sqrt{2}}=-\frac{1+p^2}{p}$
• Fall 2: $-\frac{1}{\sqrt{2}}-\frac{2}{\sqrt{2}}=-\frac{1+p^2}{p}$

Lös nu ut $p$ ur dessa ekvationer så är du nästan klar.

Yngve skrev:

 

• Fall 1: $\frac{1}{\sqrt{2}}+\frac{2}{\sqrt{2}}=-\frac{1+p^2}{p}$

För detta fall får jag $\pm \sqrt{5}$

• Fall 2: $-\frac{1}{\sqrt{2}}-\frac{2}{\sqrt{2}}=-\frac{1+p^2}{p}$

Jag erhåller ingen reell rot för denna ekvation.

Så vad kan man dra för slutsats? Att summan av de reella rötterna är 0?

Dani163 skrev:

Yngve skrev:

 

• Fall 1: $\frac{1}{\sqrt{2}}+\frac{2}{\sqrt{2}}=-\frac{1+p^2}{p}$

För detta fall får jag $\pm \sqrt{5}$

Hur får du det? Visa din uträkning.

• Fall 2: $-\frac{1}{\sqrt{2}}-\frac{2}{\sqrt{2}}=-\frac{1+p^2}{p}$

Jag erhåller ingen reell rot för denna ekvation.

Samma här, visa din uträkning.

Yngve skrev:

Dani163 skrev:

Visa föregående citat

Yngve skrev:

 

• Fall 1: $\frac{1}{\sqrt{2}}+\frac{2}{\sqrt{2}}=-\frac{1+p^2}{p}$

För detta fall får jag $\pm \sqrt{5}$

Hur får du det? Visa din uträkning.

• Fall 2: -\frac{1}{\sqrt{2}}-\frac{2}{\sqrt{2}}=-\frac{1+p^2}{p}$</p><p>$

Jag erhåller ingen reell rot för denna ekvation.

Samma här, visa din uträkning.

Det verkar ha blivit något fel på formateringen i det du skrev.

Kan du skriva för hand och ladda upp en bild?

Yngve skrev:

Det verkar ha blivit något fel på formateringen i det du skrev.

Kan du skriva för hand och ladda upp en bild?

Skrev upp koden på Overleaf och det funkade utmärkt. Har ändrat mitt inlägg. Hoppade över några steg vid $3 p \cdot \sqrt{2}+2 p^2+2=0$.

Bra, nu stämmer det.

Kommer du vidare?

Yngve skrev:

Bra, nu stämmer det.

Kommer du vidare?

Det största och det minsta p har summan 0? 

$-\sqrt{2} + \sqrt{2} = 0$

Eller har jag hoppat över någon steg?

Jag får samma resultat.