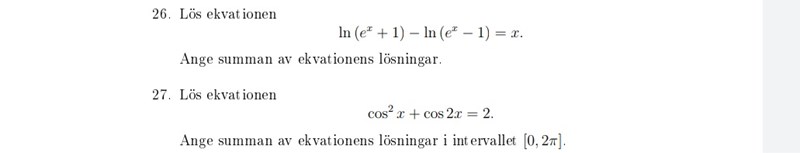MAFY 2022 uppgift 27

Hej!

Det är ett intervall, med ändpunkterna inkluderade. $x\in\left[0,2\pi\right]$ är ekvivalent med att $0\leq x\leq 2\pi$.

Moffen skrev:

Hej!

Det är ett intervall, med ändpunkterna inkluderade. $x\in\left[0,2\pi\right]$ är ekvivalent med att $0\leq x\leq 2\pi$.

Ok så vad betyder frågan? Jag förstår att x kan vara lika med 0,större än 0 eller lika med 2pi, mindre än 

Eftersom cosinus är en periodisk funktion så finns det oändligt många lösningar, så det är inte riktigt betydelsefullt att prata om summan av alla lösningar. Därför ber dom er att hitta alla lösningar $x$ sådana att $0\leq x\leq 2\pi$, för att sedan beräkna summan av alla lösningar (i det intervallet).

Moffen skrev:

Eftersom cosinus är en periodisk funktion så finns det oändligt många lösningar, så det är inte riktigt betydelsefullt att prata om summan av alla lösningar. Därför ber dom er att hitta alla lösningar $x$ sådana att $0\leq x\leq 2\pi$, för att sedan beräkna summan av alla lösningar (i det intervallet).

Okej alltså jag fick 2 lösningar i intervallet. Svaret är 3pi,men jag förstår ej varför 

Vilka är dina lösningar? Vad är summan? 

Jag kan, utan att räkna, se åtminstone 3 lösningar i intervallet $\left[0,2\pi\right]$ så du måste ha missat någon.

Moffen skrev:

Vilka är dina lösningar? Vad är summan? 

Jag kan, utan att räkna, se åtminstone 3 lösningar i intervallet $\left[0,2\pi\right]$ så du måste ha missat någon.

Jag fick cos^2x+cos^2x-sin^2x=2

2cos^2x-1+cos^x=2 

3cos^2x=3 

Cos^2x=1 

Cosx=pi eller cosx= 2pi eller 0 

Vilken är tredje lösningen? 

Kom ihåg att cosinus är en periodisk funktion, så om $x=2\pi$ är en lösning så är även $x=2\pi-2\pi=0$ en lösning.

Moffen skrev:

Kom ihåg att cosinus är en periodisk funktion, så om $x=2\pi$ är en lösning så är även $x=2\pi-2\pi=0$ en lösning.

Hur menar du? Menar du att cos0=1? Jag missade att cos0 ger 1 och cos2pi ger också 1 medan cospi ger mig - 1

Du har själv kommit fram till att $x=2\pi$ är en lösning, eller hur? Sen gäller att om du har en lösning $x$ att även $x+2n\pi$ är en lösning för heltal $n$. Välj $n=-1$ så får du att $x=0$ är en lösning.

Vad är sen summan av dina lösningar?

Moffen skrev:

Du har själv kommit fram till att $x=2\pi$ är en lösning, eller hur? Sen gäller att om du har en lösning $x$ att även $x+2n\pi$ är en lösning för heltal $n$. Välj $n=-1$ så får du att $x=0$ är en lösning.

Vad är sen summan av dina lösningar?

Jaha men jag kom fram till att x=2pi och pi som jag sa. Man drar ju roten ur på båda leden och får 2 lösningar +-

Ja man kan prova att stoppa in n=0,1 osv 

Moffen skrev:

Du har själv kommit fram till att $x=2\pi$ är en lösning, eller hur? Sen gäller att om du har en lösning $x$ att även $x+2n\pi$ är en lösning för heltal $n$. Välj $n=-1$ så får du att $x=0$ är en lösning.

Vad är sen summan av dina lösningar?

Summan är väl 3 då pi+2pi +0. 

Summan är $0+\pi+2\pi=3\pi$, vilket jag antar är vad du menar.

Moffen skrev:

Summan är $0+\pi+2\pi=3\pi$, vilket jag antar är vad du menar.

Jaa precis.