Mafy 2022 Uppgift 6
Jag har en fråga angående en uppgift som handlar om att beräkna skillnaden i energi mellan två tillstånd i väteatomen. Uppgiften lyder:
Övergången mellan tillstånden och 1s i väte kallas för Lyman--linjen. På grund av kopplingen mellan elektronens spinn och rörelsemängdsmoment delas nivån upp i två tillstånd, och . Våglängderna för det ljus som skickas ut vid övergång från dessa två tillstånd till tillståndet är respektive . Hur stor är skillnaden i energi mellan tillstånden och ?

Jag har försökt lösa uppgiften genom att använda formeln , där står för energi, är Plancks konstant och är frekvensen. Jag omvandlade sedan våglängderna till frekvenser genom att använda formeln , där är ljusets hastighet. Därefter beräknade jag skillnaden mellan energierna för de två tillstånden genom att subtrahera dem från varandra.
Men jag undrar varför jag behöver använda för varje våglängd och sedan ta differensen mellan de två energierna? Varför kan jag inte bara använda , där är skillnaden i våglängderna för de två övergångarna?
Tack på förhand för hjälpen!
Alternativen att välja på i uppgiften är:
A.
B.
C.
D. Kan ej avgöras utan information om energin för tillståndet 1s.
Dani163 skrev:Varför kan jag inte bara använda , där är skillnaden i våglängderna för de två övergångarna?
Det gäller ju inte.
Däremot gäller i mycket bra approximation att
Det nämns i frågan att våglängderna för övergångarna från och till tillståndet i väteatomen skiljer sig åt i femte decimalen. Detta innebär att skillnaden i våglängd mellan de två övergångarna är mycket liten, och därmed är också skillnaden i energierna mellan de två tillstånden mycket liten.
Energin för en foton ges av
Differentialen av skalären är
Med insatta värden får vi
Man kan faktiskt strunta i de gällande siffrorna och ändå klura ut vilket svarsalternativ som gäller eftersom det enda man behöver göra är att träffa rätt på några tiopotenser när.
D4NIEL skrev:Energin för en foton ges av
Differentialen av skalären är
Med insatta värden får vi
Man kan faktiskt strunta i de gällande siffrorna och ändå klura ut vilket svarsalternativ som gäller eftersom det enda man behöver göra är att träffa rätt på några tiopotenser när.
Varför kan man ej köra på det här sättet nedan och varför delar man med vågländerna ?
Om man har tillgång till en räknare eller en dator kan man göra så. Men på det här provet är räknare inte ett tillåtet hjälpmedel . Skillnaden mellan och är inte jättestor.
Ska man använda huvudräkning och enkla överslag är det fördelaktigt att studera differentialen (tycker jag). Testa att räkna på båda sätt och se om du själv upplever någon skillnad.
D4NIEL skrev:Om man har tillgång till en räknare eller en dator kan man göra så. Men på det här provet är räknare inte ett tillåtet hjälpmedel . Skillnaden mellan och är inte jättestor.
Ska man använda huvudräkning och enkla överslag är det fördelaktigt att studera differentialen (tycker jag). Testa att räkna på båda sätt och se om du själv upplever någon skillnad.
Aa jag förstår. Men jag får tyvärr 0 när jag avrundar till 122 så delta E= 1/122-1/22*hc. Differentialmetoden förstod jag ej riktigt.
destiny99 skrev:Differentialmetoden förstod jag ej riktigt.
Det går bra med Det innebär att om våglängden är en procent längre måste frekvensen (och energin) vara en procent mindre, i bra approximation.
Så använd bara att
Pieter Kuiper skrev:destiny99 skrev:Differentialmetoden förstod jag ej riktigt.
Det går bra med Det innebär att om våglängden är en procent längre måste frekvensen (och energin) vara en procent mindre, i bra approximation.
Så använd bara att
Men lambda nämnaren ,är det då första våglängden? Alltså 121,5668-121,5674/121,5668?
destiny99 skrev:Men lambda nämnaren ,är det då första våglängden? Alltså 121,5668-121,5674/121,5668?
Det spelar (nästan) ingen roll. Här kan det duga med att skriva 120 nm. Eller 100 nm.
Pieter Kuiper skrev:destiny99 skrev:Differentialmetoden förstod jag ej riktigt. Det går bra med Det innebär att om våglängden är en procent längre måste frekvensen (och energin) vara en procent mindre, i bra approximation.
Är detta en korrekt härledning av formeln?
Fotoners energi , där $h$ är Plancks konstant, är ljusets hastighet och är fotonens våglängd.
Vi antar att en foton emitteras från ett atomärt eller molekylärt system i en övre energinivå med energin och sedan övergår till en lägre energinivå med energin genom att utsända en foton med våglängden . Då kan vi uttrycka skillnaden i energi mellan de två nivåerna som .
Från formeln för fotoners energi kan vi skriva om detta som . Vi bryter ut hc:
Därefter kan vi dela båda sidor av ekvationen med eller och ersätta med :
Här blev jag dock osäker på hur man skulle fortsätta.
Dani163 skrev:Pieter Kuiper skrev:destiny99 skrev:Differentialmetoden förstod jag ej riktigt. Det går bra med Det innebär att om våglängden är en procent längre måste frekvensen (och energin) vara en procent mindre, i bra approximation.
Är detta en korrekt härledning av formeln?
Fotoners energi , där $h$ är Plancks konstant, är ljusets hastighet och är fotonens våglängd.
Vi antar att en foton emitteras från ett atomärt eller molekylärt system i en övre energinivå med energin och sedan övergår till en lägre energinivå med energin genom att utsända en foton med våglängden . Då kan vi uttrycka skillnaden i energi mellan de två nivåerna som .
Från formeln för fotoners energi kan vi skriva om detta som . Vi bryter ut hc:
Därefter kan vi dela båda sidor av ekvationen med eller och ersätta med :
Här blev jag dock osäker på hur man skulle fortsätta.
Ska det ej vara delat med E1 ( E2-E1/E1) och sen lambda2-lambda1/lambda1?
destiny99 skrev:Dani163 skrev:Pieter Kuiper skrev:destiny99 skrev:Differentialmetoden förstod jag ej riktigt. Det går bra med Det innebär att om våglängden är en procent längre måste frekvensen (och energin) vara en procent mindre, i bra approximation.
Är detta en korrekt härledning av formeln?
Fotoners energi , där $h$ är Plancks konstant, är ljusets hastighet och är fotonens våglängd.
Vi antar att en foton emitteras från ett atomärt eller molekylärt system i en övre energinivå med energin och sedan övergår till en lägre energinivå med energin genom att utsända en foton med våglängden . Då kan vi uttrycka skillnaden i energi mellan de två nivåerna som .
Från formeln för fotoners energi kan vi skriva om detta som . Vi bryter ut hc:
Därefter kan vi dela båda sidor av ekvationen med eller och ersätta med :
Här blev jag dock osäker på hur man skulle fortsätta.
Ska det ej vara delat med E1 ( E2-E1/E1) och sen lambda2-lambda1/lambda1?
Ja, det låter mer korrekt.
Dani163 skrev:Pieter Kuiper skrev:
Det går bra med Det innebär att om våglängden är en procent längre måste frekvensen (och energin) vara en procent mindre, i bra approximation.
Är detta en korrekt härledning av formeln?
Fotoners energi , där $h$ är Plancks konstant, är ljusets hastighet och är fotonens våglängd.
Vi antar att en foton emitteras [...]
Detta beror inte alls på atomära energinivåer osv.
Om produkt av tryck och volym är konstant innebär det att om man minskar volymen med en procent då går trycket upp med en procent.
Det är enkla räkneregler som man brukade använda vid huvudräkning. Ja, man kan göra det med matematik och serieutveckla om osv.
Men det här är fysik som går ut på att snabbt välja bort felaktiga svar. Hur matematiskt korrekt det är behöver man inte bry sig om.
Pieter Kuiper skrev:Det är enkla räkneregler som man brukade använda vid huvudräkning. Ja, man kan göra det med matematik och serieutveckla om osv.
Jag vet inte vad du syftar på här, pratar vi om härledningen av ?
Apropå funktionen som du approximerade, om x är mycket mindre än 1, betyder det inte då att vi får 1/1 = 1, då x är negligerbar i bråket.
Jag har inte hunnit så långt att ha lärt mig om "serieutveckling" än.
Dani163 skrev:Jag har inte hunnit så långt att ha lärt mig om "serieutveckling" än.
Min poäng var att man inte behöver serieutveckling för att veta att osv.
Det var sådana räkneregler som vi brukade använda innan miniräknare.
I inlägg #11 har ni kommit fram till att
Som det står är uttrycket lite tråkigt att hantera med huvudräkning, men vi kan skriva om det. Först sätter vi allt på ett gemensamt bråkstreck:
Med alltså
Nu gäller det att inse att det faktiskt inte spelar så stor roll om vi delar med 121.5668 eller 121.5674 i nämnaren.. Vi ersätter helt enkelt i nämnaren, t.ex.
Slutligen kommer vi ihåg att varvid
D4NIEL skrev:Slutligen kommer vi ihåg att varvid
Okej, så med följande våglängder:
för övergång från tillståndet till -tillståndet.
för övergång från tillståndet till -tillståndet.
Använder vi ekvationen från citatet:
där är energin för en foton med våglängd och och är Plancks konstant respektive ljusets hastighet i vakuum. Våglängdsdifferensen är . Sedan sätter vi in värdena i ekvationen:
Tänkte du att förenklingen skulle se ut något i den stilen?
Slår jag in det i Wolfram Alpha får jag följande:

Och:
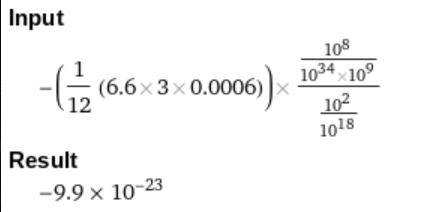
Dani163 skrev:Använder vi ekvationen från citatet:
Tänkte du att förenklingen skulle se ut något i den stilen?Slår jag in det i Wolfram Alpha får jag följande:
Det blir för komplicerat. Dessa uppgifter ska lösas utan Wolfram eller miniräknare.
Så
Sedan behöver man fotonernas energi i eV, eller i alla fall dess storleksordning. Ljus (synligt och UV) har fotonenergier på enstaka eV och det räcker då för att välja rätt svar.
Lite mer exakt vet man kanske att ionisationsenergi av väte är 13,6 eV och att övergången från n=2 till n=1 har då en energi
Så att rätt svar är alternativ B.


