Mängdlära?

64 elever tillfrågades om vilka av ämnena bild, musik eller foto de läser som individuellt val. Resultatet visade att 14 läser bild, 20 musik och 17 foto. Det visade också att 4 läser både musik och bild, 6 både bild och foto och 9 både musik och foto, 2 elever läser alla tre.

a) Beräkna hur många av de tillfrågade eleverna som inte läser något av ämnena.

b) Beräkna hur många som har enbart bild

Min lösning:

a) får jag till 64 - 34 dvs = 30 som inte läser något

b) elever som läser bild: 14 - 4 - 6 + 2 =6

Det får jag också, så vi kanske har rätt båda två. Vill du ha synpunkter på din uträkning av (a) får du posta den. Vad gäller (b) räknade jag som du.

Venn-diagram?

Trinity2 skrev:
Venn-diagram?

Vet inte hur TS gjorde, men själv tog jag tillfället att repetera lite linjär algebra:

import numpy as np

variables = [
    "x (Bild)",
    "y (Musik)",
    "z (Foto)",
    "a (Bild+Musik)",
    "b (Bild+Foto)",
    "c (Musik+Foto)",
    "d (Bild+Musik+Foto)"
    ]

A = np.array([
    [1, 0, 0, 1, 1, 0, 1],  # x + a + b + d = 14
    [0, 1, 0, 1, 0, 1, 1],  # y + a + c + d = 20
    [0, 0, 1, 0, 1, 1, 1],  # z + b + c + d = 17
    [0, 0, 0, 1, 0, 0, 1],  # a + d = 4
    [0, 0, 0, 0, 1, 0, 1],  # b + d = 6
    [0, 0, 0, 0, 0, 1, 1],  # c + d = 9
    [0, 0, 0, 0, 0, 0, 1]   # d = 2
])

B = np.array([14, 20, 17, 4, 6, 9, 2])

solution = np.linalg.solve(A, B)

for var, val in zip(variables, solution):
    print(f"{var}: {int(val)}")

print(f"\nAntal som inte läser något tillval: {64 - int(sum(solution))}")

x (Bild): 6
y (Musik): 9
z (Foto): 4
a (Bild+Musik): 2
b (Bild+Foto): 4
c (Musik+Foto): 7
d (Bild+Musik+Foto): 2

Antal som inte läser något tillval: 30

Alltid imponerad över era fina programmeringskunskaper, som jag saknar helt.

här är en manuell lösning

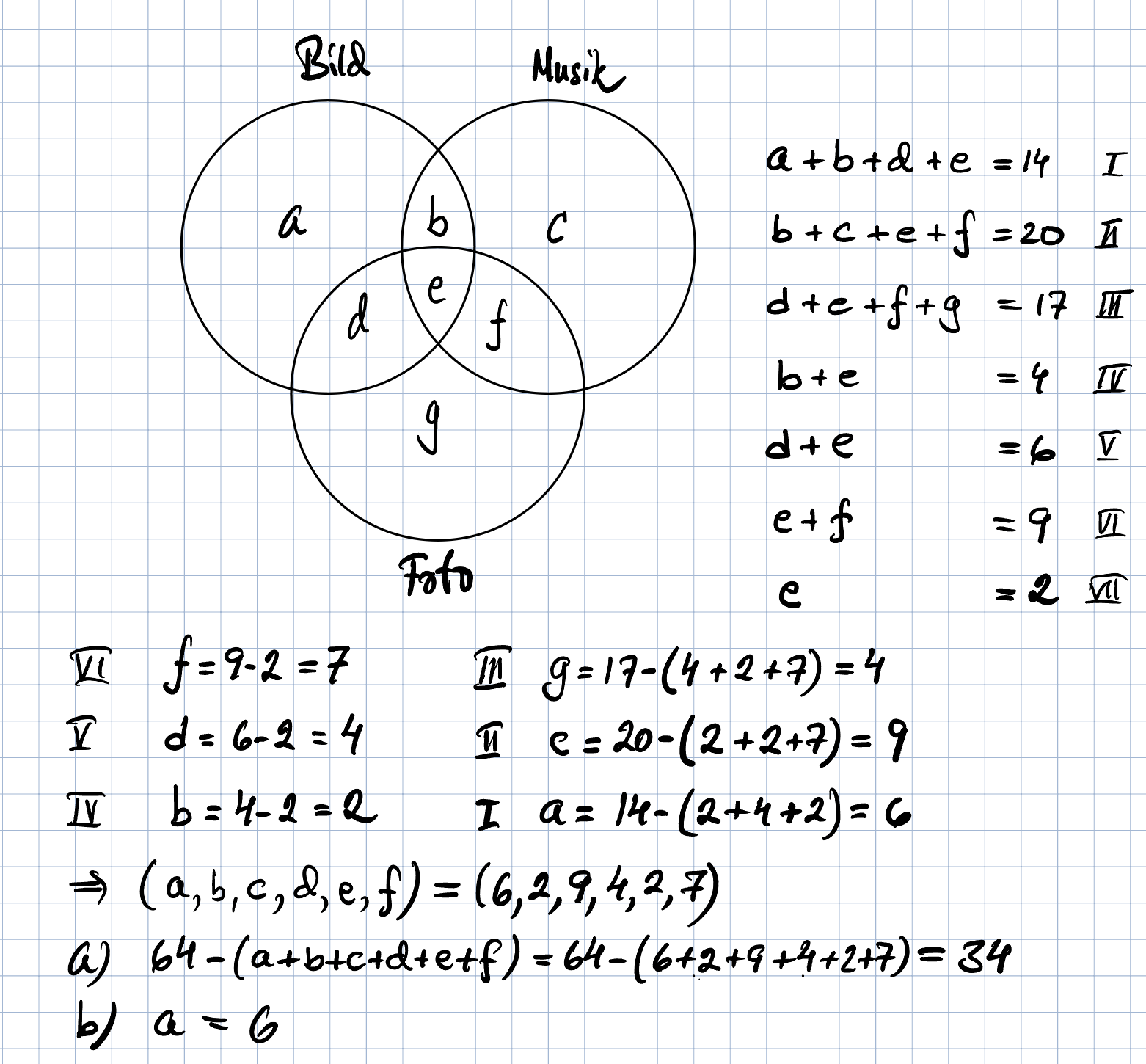
Trinity2 skrev:
Alltid imponerad över era fina programmeringskunskaper, som jag saknar helt.

här är en manuell lösning

Du fick 34 på a) men då har jag nog gjort fel då jag fick 30 ?

Jag har slarvat. Du har rätt. Jag har glömt g på slutet. Illa. Skall vara 30.

Så här blir min matris i Mathematica.

Trinity2, du som sade du inte kunde programmering. Det där ser ju ut som min python, näsan rakt av ju. :-)

Python 3.12.8 (tags/v3.12.8:2dc476b, Dec  3 2024, 19:30:04) [MSC v.1942 64 bit (AMD64)] on win32
Type "help", "copyright", "credits" or "license()" for more information.
import numpy as np
A = np.array([
    [1, 0, 0, 1, 1, 0, 1],  # x + a + b + d = 14
    [0, 1, 0, 1, 0, 1, 1],  # y + a + c + d = 20
    [0, 0, 1, 0, 1, 1, 1],  # z + b + c + d = 17
    [0, 0, 0, 1, 0, 0, 1],  # a + d = 4
    [0, 0, 0, 0, 1, 0, 1],  # b + d = 6
    [0, 0, 0, 0, 0, 1, 1],  # c + d = 9
    [0, 0, 0, 0, 0, 0, 1]   # d = 2
])
B = np.array([14, 20, 17, 4, 6, 9, 2])
solution = np.linalg.solve(A, B)
solution
array([6., 9., 4., 2., 4., 7., 2.])
64-int(sum(solution))
30

sictransit skrev:

Trinity2, du som sade du inte kunde programmering. Det där ser ju ut som min python, näsan rakt av ju. :-)

Python 3.12.8 (tags/v3.12.8:2dc476b, Dec  3 2024, 19:30:04) [MSC v.1942 64 bit (AMD64)] on win32
Type "help", "copyright", "credits" or "license()" for more information.
import numpy as np
A = np.array([
    [1, 0, 0, 1, 1, 0, 1],  # x + a + b + d = 14
    [0, 1, 0, 1, 0, 1, 1],  # y + a + c + d = 20
    [0, 0, 1, 0, 1, 1, 1],  # z + b + c + d = 17
    [0, 0, 0, 1, 0, 0, 1],  # a + d = 4
    [0, 0, 0, 0, 1, 0, 1],  # b + d = 6
    [0, 0, 0, 0, 0, 1, 1],  # c + d = 9
    [0, 0, 0, 0, 0, 0, 1]   # d = 2
])
B = np.array([14, 20, 17, 4, 6, 9, 2])
solution = np.linalg.solve(A, B)
solution
array([6., 9., 4., 2., 4., 7., 2.])
64-int(sum(solution))
30

Det är enklare att skriva lite kommando i Mathematica än att hantera objektsmodeller och instanser och typklasser m.m. Helt 'lost' här... :)

Svara

Visa senaste svar