Markera i det komplexa talplanet de komplexa tal z för...

Det ser ut satt ha smugit sig in ett extra minstecken i slutet (ellerså fattas det en term). Vad betyder ekvationen? Vad betyder |z-4|? Vad betyder |z-2i|?

Du kan ju prova lite på gammalt vis. Jo, jag läste matematik för längesedan! Alla punkter  |z-4|  ligger på en cirkel. Rita in punkten 4 och 2i. Ta en passare och rita in en cirkel med radien ex 5 och en med radien ex 10. Där de möts är villkoret uppfyllt. Ser du något mönster? Blir svaret en cirkel, parabel eller något annat?

Det betyder att avståndet ska vara lika.

Precis. Ekvationen beskriver alla punkter med samma avstånd till 4 som till 2i. Vilka punkter är det?

Ett annat sätt att angripa problemet, utan att tänka först, är att skriva z på rektangulär form, använda Pythagoras sats för att utveckla beloppen, och börja räkna.

Jag skulle behöva mer hjälp.

Jag hjälper dig igång med "räkna räkna räkna"-metoden som haraldfreij tipsade om.

Sätt $z=a+bi$.

Då är

• $z-4=(a-4)+bi$ och $|z-4|=\sqrt{(a-4)^2+b^2}$
• $z-2i=a+(b-2)i$ och $|z-2i|=\sqrt{a^2+(b-2)^2}$

Ekvationen $|z-4|=|z-2i|$ kan då skrivas

$\sqrt{(a-4)^2+b^2}=\sqrt{a^2+(b-2)^2}$

Kommer du vidare därifrån?

Protjon1 skrev:

Jag skulle behöva mer hjälp.

Har du ritat in punkterna i ett koordinatsystem och ritat som jag tipsade om?

Då fick jag fram 3= 2a-b.

Protjon1 skrev:

Då fick jag fram 3= 2a-b.

OK, och kan du dra några slutsatser av det?

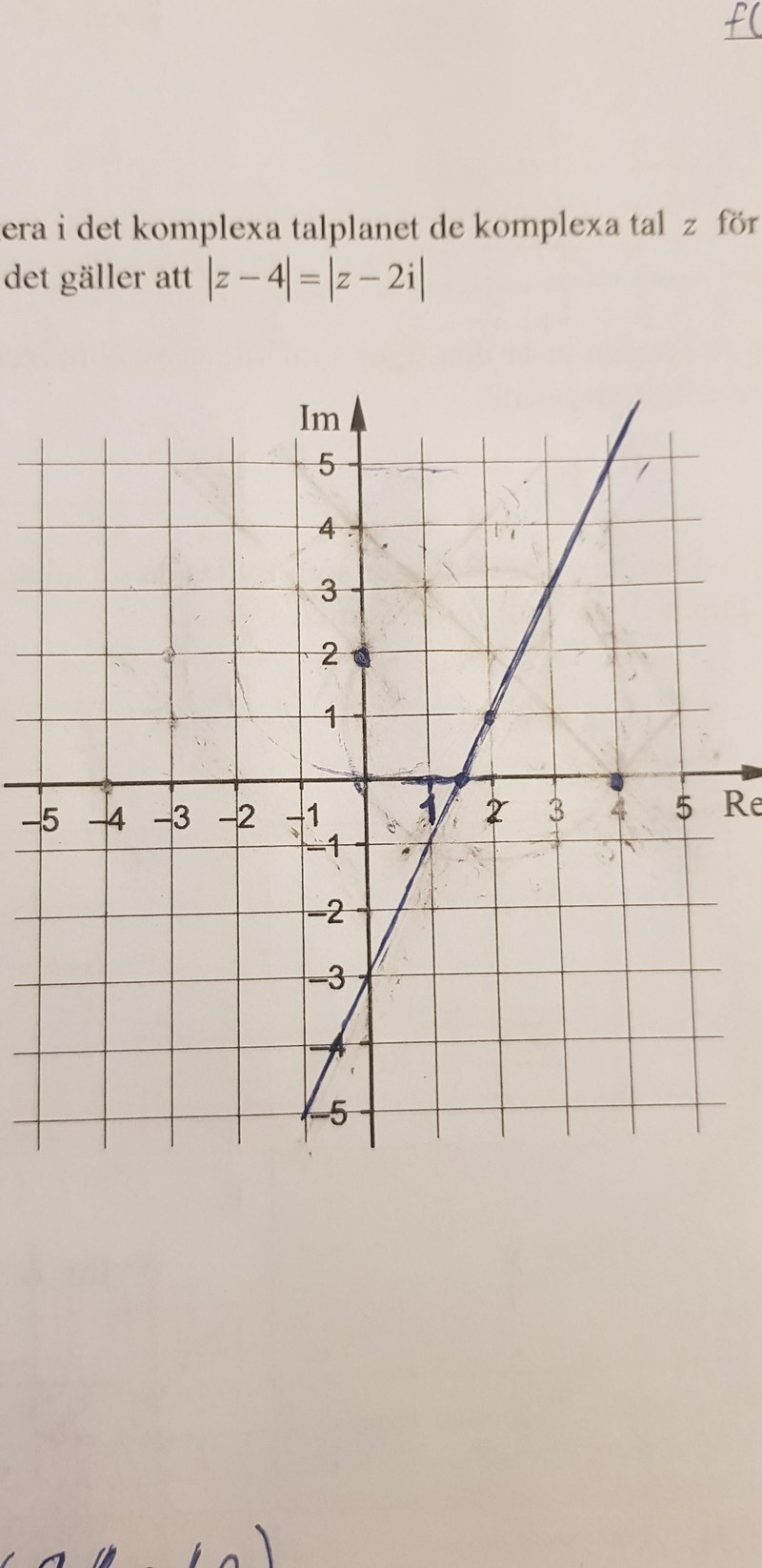
Jag vet inte. Jag har fått fram en linje, y=1,5x-3.

Vad gäller för punkter på den linjen, där y står för Im-axeln och x för Re-axeln i det komplexa talplanet.
Testa villkoret i uppgiften för t ex punkten (0,-3)

Protjon1 skrev:

Jag vet inte. Jag har fått fram en linje, y=1,5x-3.

Du har räknat ut att alla komplexa tal z = a + bi som uppfyller villkoret b = 2a - 3 även uppfyller villkoret |z - 3| = |z - 2i|.

Du har konstaterat att alla komplexa tal z = a + bi som uppfyller villkoret b = 2a - 3 ligger på en linje i det komplexa talplanet.

Det betyder att alla komplexa tal z = a + bi som ligger på den linjen uppfyller villkoret z - 3| = |z - 2i|.

Avståndet är lika, innebär detta att jag har löst uppgiften?

Protjon1 skrev:

Avståndet är lika, innebär detta att jag har löst uppgiften?

Uppgiften gäller att markera komplexa tal i det komplexa talplanet. Gör gärna det och visa din bild.

Det stämmer. Snyggt!