Markera i en figur de komplexa tal z...

Hej. Har löst denna uppgift (tror jag) men förstår inte hur svaret kan vara rätt. Enbart genom att titta på frågan ska alltså talet z både ha sin imaginär strikt större än noll (villkor 1) och samtidigt mindre än/lika med noll (villkor 2). Hur går det ihop? Mitt svar:
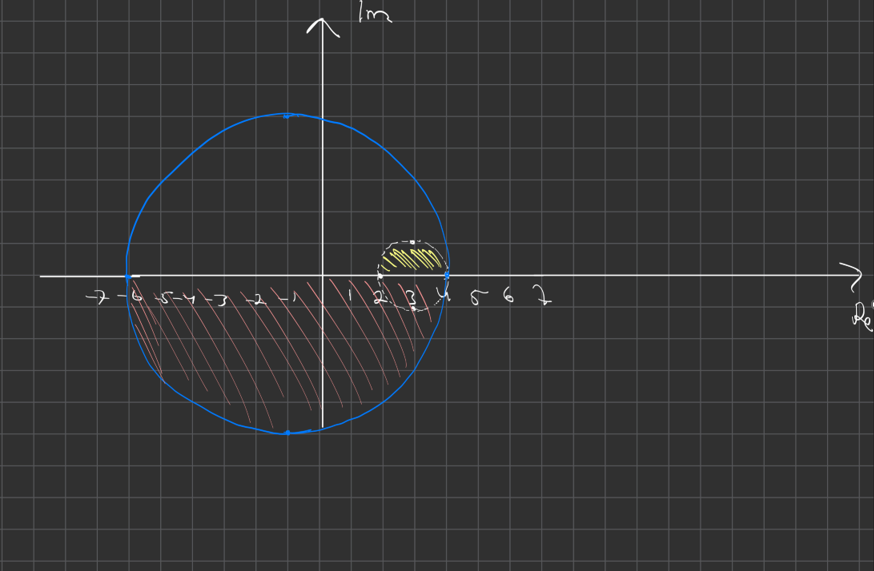
Den gula delen uppfyller villkor 1 och den rosa delen uppfyller villkor 2, men de har inte något gemensamt område då den ena befinner sig över x - axeln och den andra under.
Vad är det jag missar?
Vad säger facit?
Om Im z > 0 gäller det första villkoret för normen av z.
Om Im z ≤ 0 gäller det andra villkoret.
Tillsammans definierar det en mängd.
Pieter Kuiper skrev:Om Im z > 0 gäller det första villkoret för normen av z.
Om Im z ≤ 0 gäller det andra villkoret.
Tillsammans definierar det en mängd.
Hur menar du?
Bedinsis skrev:Vad säger facit?
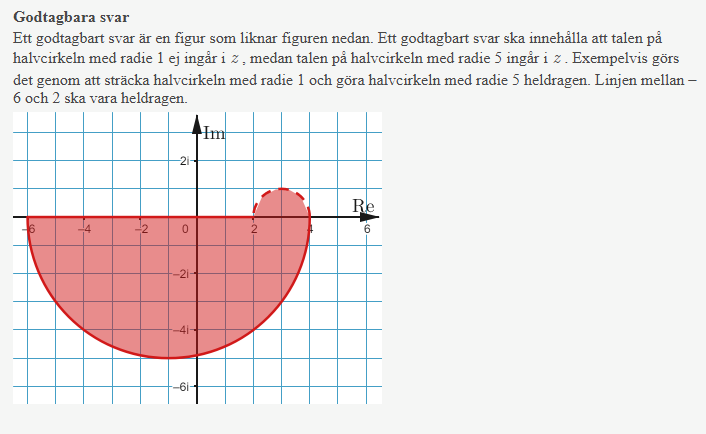
Ser du att svaret i facit stämmer överens med det område du har markerat I trådstarten?
Anonym_15 skrev:Pieter Kuiper skrev:Om Im z > 0 gäller det första villkoret för normen av z.
Om Im z ≤ 0 gäller det andra villkoret.
Tillsammans definierar det en mängd.Hur menar du?
Jag menar det som står i uppgiften, som man också ser i facit.
Det är på ungefär samma sätt som man definierar en funktion abs(x):
* abs(x) = -x när x ≤ 0
* abs(x) = x när x > 0.
Yngve skrev:Ser du att svaret i facit stämmer överens med det område du har markerat I trådstarten?
Ja precis, men det finns inget gemensamt område? Dvs. någonstans där områdena överlappar varandra. Det är det jag trodde innebar att båda villkoren skulle gälla samtidigt. Eller så kanske jag missuppfattar frågan.
Anonym_15 skrev:Yngve skrev:Ser du att svaret i facit stämmer överens med det område du har markerat I trådstarten?
Ja precis, men det finns inget gemensamt område? Dvs. någonstans där områdena överlappar varandra. Det är det jag trodde innebar att båda villkoren skulle gälla samtidigt. Eller så kanske jag missuppfattar frågan.

Anonym_15 skrev:det finns inget gemensamt område? Dvs. någonstans där områdena överlappar varandra. Det är det jag trodde innebar att båda villkoren skulle gälla samtidigt. Eller så kanske jag missuppfattar frågan.
Du missuppfattar frågan.
Hur uppfattar du denna definition?
Frågan är dåligt formulerad eftersom man inte angett något logiskt konnektiv mellan villkoren. Svårt att veta om man vill ha snitt eller union av de områden som definieras av respektive villkor.
Pieter Kuiper skrev:Anonym_15 skrev:det finns inget gemensamt område? Dvs. någonstans där områdena överlappar varandra. Det är det jag trodde innebar att båda villkoren skulle gälla samtidigt. Eller så kanske jag missuppfattar frågan.
Du missuppfattar frågan.
Hur uppfattar du denna definition?
Den ser ut som ett V:
-
Lutning −1 för x≤0
-
Lutning +1 för x>0
-
Och en spets i origo (0,0)
En s.k. absolutbeloppsfunktion?
Anonym_15 skrev:Pieter Kuiper skrev:Anonym_15 skrev:det finns inget gemensamt område? Dvs. någonstans där områdena överlappar varandra. Det är det jag trodde innebar att båda villkoren skulle gälla samtidigt. Eller så kanske jag missuppfattar frågan.
Du missuppfattar frågan.
Hur uppfattar du denna definition?Den ser ut som ett V:
Lutning −1 för x≤0
Lutning +1 för x>0
Och en spets i origo (0,0)
En s.k. absolutbeloppsfunktion?
Ja.
Så läs den här uppgiften på samma sätt. Det ena villkoret gäller om punkten ligger på ena sidan av den reella axeln, det andra villkoret gäller om punkten ligger på den andra sidan.




