Markering av komplexa tal i talsystemet
Hej! Jag har så svårt att förstå hur jag ska tänka i följande uppgift:
Jag ska markera komplexa tal z idet komplexa talsystemet för vilka det gäller att |z - 1 + 2i| = |z - 2|. Jag förstår att det gäller avstånd mellan z och (1 + 2i) på vänster sida, men hur går jag vidare?
Ja, eller |z-(1-2i)| är avståndet 1-2i. Detta ska tydligen vara lika stort som avståndet till 2. Kan du markera detta i det komplexa talplanet på något sätt?
Du kan också börja med att anta
Varför blir det 1 - 2i istället? Är det för att det är negativ mellan z och uttrycket?
För reella tal a och b gäller att |a-b| kan tolkas som avståndet mellan talen a och b.
I det komplexa fallet gäller det att |z-w| kan tolkas som avståndet mellan de två komplexa talen z och w.
=======
Svar på din fråga: Ja, eftersom -1+2i = -(1+2i).
Det betyder att |z-1+2i| kan skrivas som |z-(1-2i)| och då alltså tolkas som avståndet mellan de två komplexa talen z och 1-2i.
Ok, tack. Så punkten från avståndet från vänstra sidan blir då (1, -2)? Avståndet på högra sidan, görs väl då om till avstånd z till 2 + 0i) med punkten (2,0). Vad gör jag med denna information nu. Är det punkter som kan bli en linje mellan dessa punkter och få fram räta linjens ekvation, y (im) = kx (re) + m? Kan jag räkna ut k-värdet genom att ta y-värdena delat på x-värdena, så att k blir 2? Kan jag sedan stoppa in ett av koordinaterna i ekvationen och få fram m-värdet?
Ett bra sätt att komma igång med svårare problem är att lösa ett enklare
fall.
Antag att
Den andra ekvationen ger
Det motsvarar punkten .
Den första ekvationen ger
Det motsvarar punkten
Så enkelt var det inte, men man kan ändra antagandet till
Antag att och
De här ekvationerna ger då
Kvadreringen ger två ekvationer:
Det är två ekvationer för två cirklar med mittpunkterna i
och och radien .
Visa spoiler
Inte viktigt: Avståndet mellan mittpunkterna är
Då måste .
I Geogebra kan man rita två cirklar med radien 2 (blå) och 4 (röda) och markera skärningspunkterna mellan dem. Man ser att punkterna kommer att bilda en rät linje (grön).
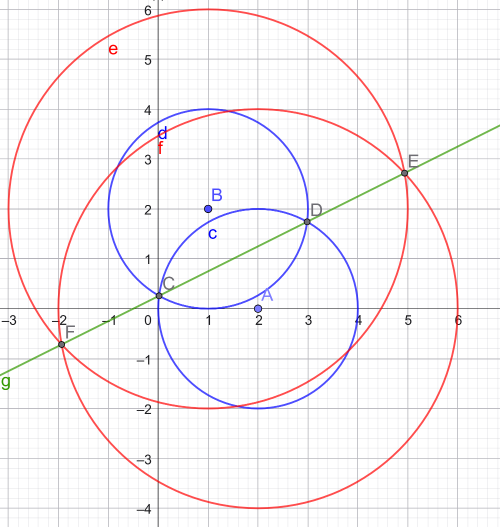
Visa spoiler
Räta linjens ekvation kan man få om man förenklar
I den här uppgiften får jag inte ha tillgång till några digitala hjälpmedel utan endast rita på papper i ett koordinatsystem. Så om jag har kommit fram till 2 punkter, hur ska jag veta vad radien till mina cirklar är då i min uppgift?
KatrinC skrev:I den här uppgiften får jag inte ha tillgång till några digitala hjälpmedel utan endast rita på papper i ett koordinatsystem. Så om jag har kommit fram till 2 punkter, hur ska jag veta vad radien till mina cirklar är då i min uppgift?
Du kommer enklare till den räta linjens ekvation på ett annat sätt. Se spoilern längst ner.
Radierna är inte så viktiga - du väljer själv vilka värden du vill arbeta med.
Som #2 säger är det punkterna 1-2i och 2. Givet att den information är rätt i #1.
Jag får följande, inga cirklar behövs,

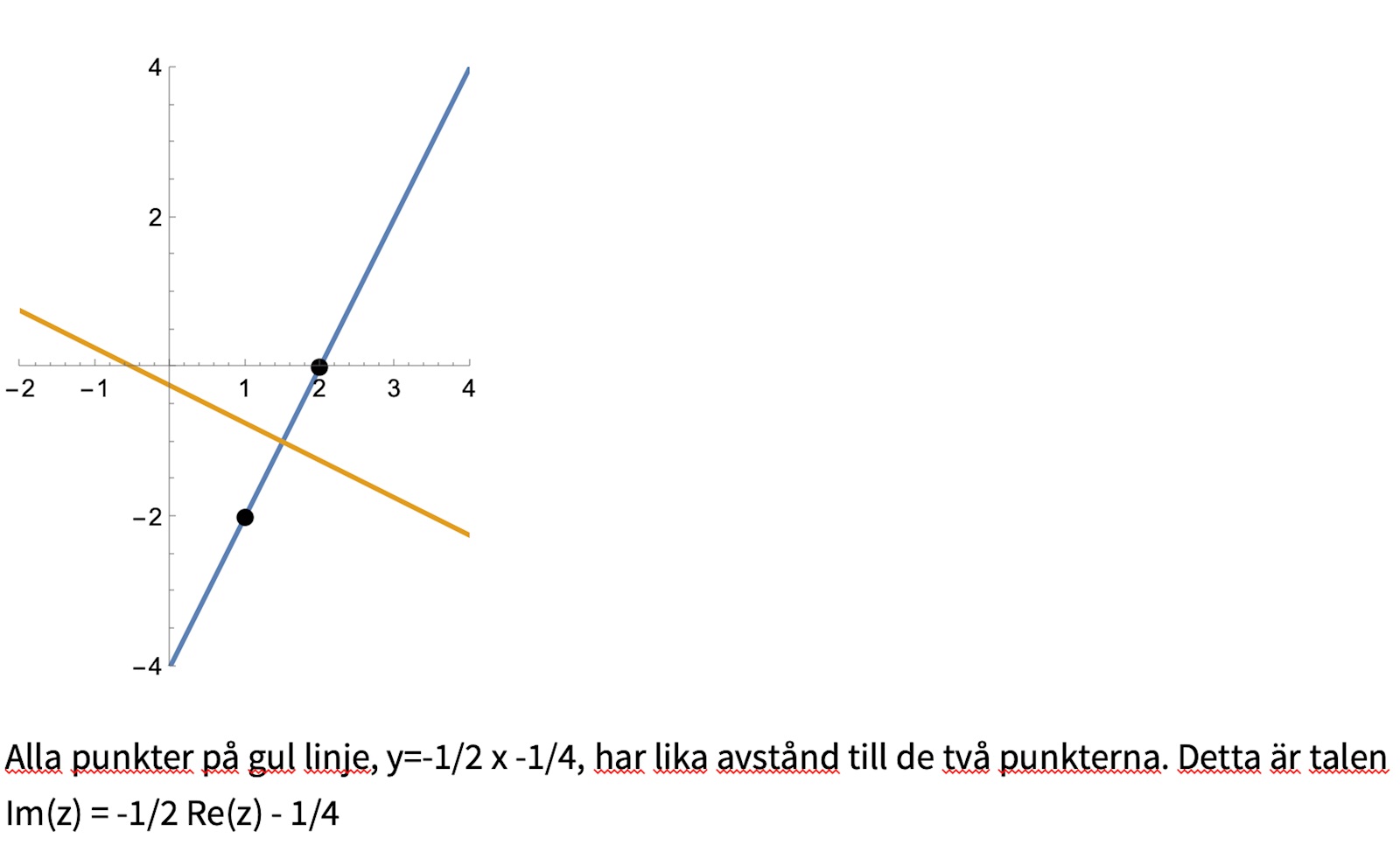
 Se grafen (som Mr P föreslog). Punkterna 1-2i och 2 är markerade. Punkter som ligger på samma avstånd från dem ligger på linjen enligt figur (gamle Euklides) i parameterform Z=1,5-i +t(1 -0,5i)
Se grafen (som Mr P föreslog). Punkterna 1-2i och 2 är markerade. Punkter som ligger på samma avstånd från dem ligger på linjen enligt figur (gamle Euklides) i parameterform Z=1,5-i +t(1 -0,5i)
Behöver inte vara krångligare.
Tack! En liten följdfråga om hur jag kom fram till den gula linjen, som skulle skära den linje jag gjort... Hur kom man fram till -4 + 2x?? jag förstår inte beräkningen där? m-värdet sedan är väl punkten där den nya linjen ska möta y-axeln? Är det fortfarande formeln y =kx + m?
KatrinC skrev:Tack! En liten följdfråga om hur jag kom fram till den gula linjen, som skulle skära den linje jag gjort... Hur kom man fram till -4 + 2x?? jag förstår inte beräkningen där? m-värdet sedan är väl punkten där den nya linjen ska möta y-axeln? Är det fortfarande formeln y =kx + m?
Vi vet att linjen har k=2 genom att beräkna lutningen m.h.a. de 2 kända punkterna.
Sedan kan vi ta en av punkterna, säg, (2,0), och beräkna linjens ekvation
y-0=2(x-2)
y=2x-4
Vi är inte så intresserade av vad som händer när linjen möter y-axeln. Du kan rita linjen direkt genom att dra en rät linje genom punkterna. (Jag vet att det är normalt att fokusera på k och m när man ritar en linje, men här har vi redan 2 punkter som linjen skall gå genom så vi gör det lätt för oss och bara drar en linje direkt.)
Ok, tack för hjälpen!



