Märklig geometriuppgift
Jag skulle vilja hitta några lösningar på nedan geometriuppgift:
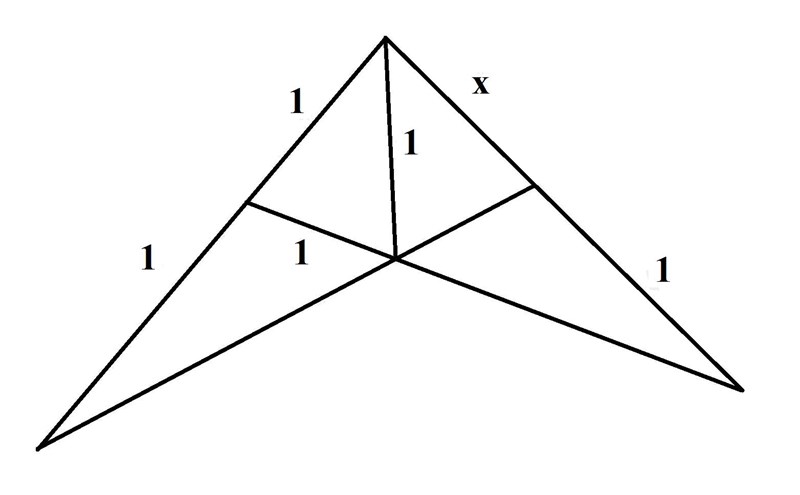
Det direkt observerbara är att den inte är skalenlig utan missvisande (troligtvis med mening). Vilka tekniker kan man använda för att lösa denna?
Edit: Jag har en lösning.
Tråd flyttad från Kluringar till Allmänna diskussioner. Kluringforumet är endast till för uppgifter du har svaret på, och vill bjuda andra på. /Smutstvätt, moderator
Tråd tillbakaflyttad till Kluringar, då det framkommit att problemet hade en lösning och var tänkt som kluring. /Smutstvätt, moderator
Om ettorna avser längden på närmaste sträcka så kan x vara vilket positivt tal som helst. De två vänstra trianglarna tillför ingen användbar information. De två högra innehåller tillräckligt många fria parametrar.
Dr. G skrev:Om ettorna avser längden på närmaste sträcka så kan x vara vilket positivt tal som helst. De två vänstra trianglarna tillför ingen användbar information. De två högra innehåller tillräckligt många fria parametrar.
Detta stämmer faktiskt inte. Jag vet att den har en entydig lösning.
De vänstra trianglarna bestämmer riktningen på linjerna till höger. Triangeln med x i bestäms därför entydigt.
Den enda lösningen jag kommer på är att börja sätta ut vinklar (man kan börja i och med att man vet att en triangel är liksidig). Sedan kan man ställa upp ekvationer med sinussatsen och Pythagoras sats och få:
vars enda lösning applicerbar för detta problem är .
Mitt svar är därför , men jag kan mycket väl ha slarvat. Det skulle såklart kännas bättre att ha en enklare lösning på problemet, men med tanke på att svaret innehåller en kubikrot är jag en smula osäker på att det ens är möjligt. Jag skulle gärna vilja veta vad Ebola har för lösning.
Det är ju alltid kul att rita.
Jag väntar till imorgon innan jag publicerar min lösning. Jag hade gärna sett någon mer än Alvins och vill inte styra försöken för mycket.
Kan man förutsätta att de båda linjerna från vardera nederhörnet till mitt på motsatt långsida är räta? Och likadant för de båda yttersidorna också, förresten.
Hur vore det att börja med att rita en skalenlig figur?
Förslag på lämpligt ritprogram?
Smaragdalena skrev:Kan man förutsätta att de båda linjerna från vardera nederhörnet till mitt på motsatt långsida är räta? Och likadant för de båda yttersidorna också, förresten.
Vad menar du med räta? De bryts inte någonstans. Alltså är vinkeln 180 grader mellan "två linjer" där de möter en annan.
Arktos skrev:Hur vore det att börja med att rita en skalenlig figur?
Förslag på lämpligt ritprogram?
Jag gjorde en skalenlig figur i Paint bara. Det hjälpte väldigt mycket för att konstruera en lösning.
Tack Ebola! Menar du MS Paint? Jag har Mac, så det går nog inte.
I begynnelsen fanns MacDraw och MacPaint men de är borta sedan länge och har inte ersatts med något annat, vad jag vet. På nätet hittade jag GeoGebra, men vi kom inte överens. Jag kan ju alltid använda papper, penna, passare o linjal, men det vore kul att konstruera figuren på skärmen. Finns det ngn bra app?
Arktos skrev:Tack Ebola! Menar du MS Paint? Jag har Mac, så det går nog inte.
I begynnelsen fanns MacDraw och MacPaint men de är borta sedan länge och har inte ersatts med något annat, vad jag vet. På nätet hittade jag GeoGebra, men vi kom inte överens. Jag kan ju alltid använda papper, penna, passare o linjal, men det vore kul att konstruera figuren på skärmen. Finns det ngn bra app?
Du kan köra med sketch.io bara:
Då trycker du på calligraphy och väljer line. Det kommer det stå hur lång linjen är vilket gör det enkelt att bygga rätt längder.
Jisses. Jag slogs i en timme med Sketch (tack för tipset!) innan jag tog fram papper och penna och en gammal gradskiva. Ganska snart hade jag ritat en (tillräckligt) skalenlig figur. Sedan satte jag ut alla vinklar jag kunde beräkna, och satt och glodde på figuren ett bra tag. Två rätvinkliga trianglar uppenbarade sig. Tricket visade sig sedan vara att dra ett par höjder och få en tredje rätvinklig triangel. Då ger det sig med sinusteoremet på den triangel som har x+1 som långsida och 1 som en av kortsidorna.
Till slut kom jag fram till samma ekvation som Alvin och samma lösning. Men denna lösning förvånar mig. Det skulle ju innebära att man kan konstruera med passare och linjal, vilket jag har för mig ska vara omöjligt (läst nånstans). Det skulle också vara skälet till att man inte kunde konstruera något praktiskt geometriskt hjälpmedel för att stämma klaver m m liksvävande, dvs med alla halvtonsteg lika stora. Då behöver man man nämligen kunna konstruera för att tolv halvtonsteg efter varandra ska bli precis en oktav.
PS Om detta skrev jag en gång en uppsats: http://ncm.gu.se/pdf/namnaren/5053_08_3.pdf
Där kommer vi till kärnan av problemet, Arktos. Varför kan Delians konstant konstrueras med detta märkliga objekt? Konstruktionen av tredjeroten ur två är ett antikt problem som ligger till grund för bland annat att fördubbla kuben (Doubling the Cube). Faktum är att tredjeroten ur två är inte ett konstruerbart tal.
Vad är det som pågår här? Visst är det märkligt? Intressant arbete förövrigt, tack för länken!
Så var det, ja. Kubens fördubbling. När jag grunnade på min konstruktion, var det en linje som kändes märklig. Det är linjen med längd x+1. Där roterade jag linjalen runt den översta punkten tills avståndet 1 passade in mellan förlängningen av de två linjerna från den vänstra triangeln. Så får man ju inte göra om man ska vara strikt. Då har man en "rätbräda" och ingen graderad linjal. Men jag kom inte på något annat sätt att konstruera linjen. Hur har Alvin och du gjort?
Redigerat: Nu har jag kollat din länk. Intressant! Och där finns ju figuren, med samma förklaring. Den som tänkte ut figuren första gången var verkligen uppfinningsrik!
Jag själv satt och lekte med geometriprogrammet, men lyckades faktiskt inte konstruera sträckan med längd . Dock tänkte jag att detta berodde på min egen oförmåga att använda programmet, men tydligen hade det en djupare betydelse.
Intressant att man inte kan konstruera med passare och ograderad linjal, men att det blir möjligt genom en ynka liten gradering på linjalen.
Som utlovat kommer min lösning här. Jag kunde hitta ett par olika varianter men den elegantaste är väldigt lik de som redan diskuterats. Om vi börjar med en skalenlig (och formenlig) figur:
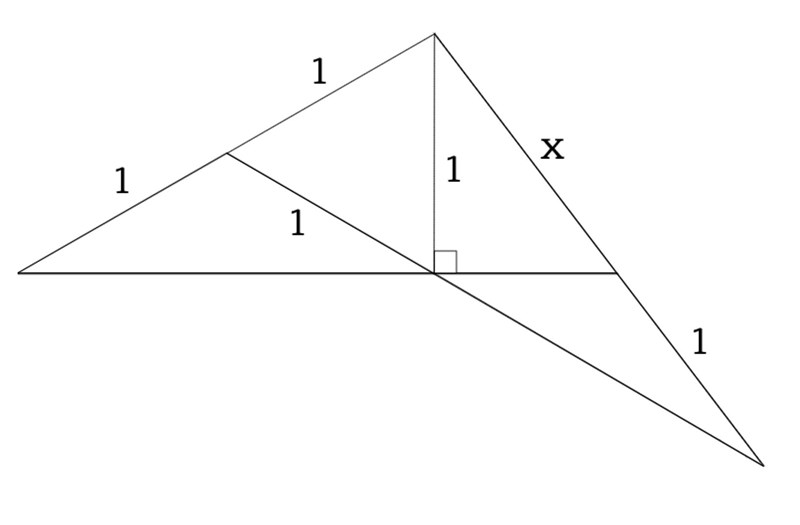
Vi kan då enkelt identifiera en rätvinklig triangel likt nedan:
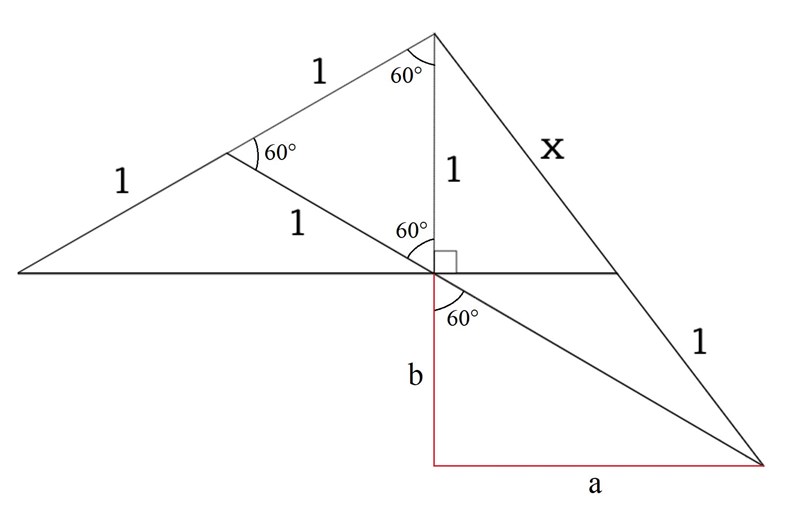
Från denna rätvinkliga triangel kan vi formulera följande relationer:
Slutligen får vi då:
Vilket efter lite jonglering ger det enda relevanta svaret som:
Detta är alltså en så kallad Neusis-konstruktion av tredjeroten ur två och det är väldigt spännande när man försöker rita en skalenlig figur. Det man märker är, precis som Alvin och Arktos nämnde, att vårt x konstrueras endast indirekt vilket är en effekt av att dess värde inte är konstruerbart.






