Masströghetsmoment

En homogen cirkulär skiva med radie R = 5,07 m och tjocklek t = 11,0 ·10-3 m roterar kring z-axeln (vinkelrät mot skivan, se figur). Ur skivans mitt är skuret ett rektangulärt hål med basen b = 4,9 m och höjden h = 4,72 m. 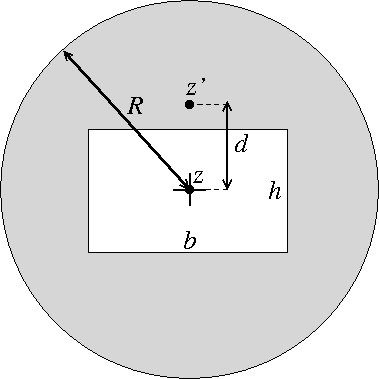Beräkna skivans masströghetsmoment omkring z-axeln om dess densitet är 6,611 kg/m³.

Formel: $I_{z z} = \frac{2}{3} M r^{2}$ , jag måste alltså hitta massan.

$m = ρ V (3 d), d ä r ρ = σ * t < = > σ = \frac{ρ}{t} m = σ A = \frac{ρ A}{t} (2 d) A = π r^{2} - b h a l l t s å : I_{z z} = \frac{2 ρ}{3 t} r^{2} (π r^{2} - b h) = v ä l d i g t s t o r t . s v a r e t ä r 68 . p å n å g o t v i s f i c k j a g ä v e n f o r m e \ln : I_{z z} = \frac{2 ρ t}{3} r^{2} (π r^{2} - b h) = 71.8 . D e t ä r o t r o l i g t m y c k e t n ä r m r e s v a r e t s o m ä r 68.988 . .$

Vad är I_zz för

en cirkel?

en rektangel?

Dr. G skrev:
Vad är I_zz för

en cirkel?

en rektangel?

För en cirkel blir det väl $\frac{2}{3} M r^{2} ? m e n ä r o s ä k e r f ö r e n r e k \tan g e l i z z .$

Cylinder:

$I_{zz}=\dfrac{1}{2}mR^2$

Rätblock:

$I_{zz}=\dfrac{1}{12}m(b^2+h^2)$

(Detta med avseende på masscentrum.)

Enklast är nog att se volymen som en cylinder plus ett rätblock med negativ densitet.

Dr. G skrev:
Cylinder:

$I_{zz}=\dfrac{1}{2}mR^2$

Rätblock:

$I_{zz}=\dfrac{1}{12}m(b^2+h^2)$

(Detta med avseende på masscentrum.)

Enklast är nog att se volymen som en cylinder plus ett rätblock med negativ densitet.

Okay rimligt. Jag antar att massan är individuell och att man få köra $m = σ A ?$

Ja, massorna ges av arean.

$m=\sigma A$

men

$\sigma = \rho\cdot t$

där t är tjockleken.

Dr. G skrev:
Ja, massorna ges av arean.

$m=\sigma A$

men

$\sigma = \rho\cdot t$

där t är tjockleken.

$I_{t o t} = \frac{1}{2} m_{c} R^{2} + \frac{1}{12} m_{r} (b^{2} + h^{2}) = \frac{ρ t A_{c}}{2} R^{2} + \frac{ρ t A_{r}}{12} (b^{2} + h^{2}) = = \frac{ρ t}{2} (A_{c} R^{2} + \frac{A_{r}}{6} (b^{2} + h^{2})) = 78 . . v a d g ö r j a g f ö r f e l ? Ä r d e t r ä t b l o c k s d e l e n t r o$

pepsi1968 skrev:
Ur skivans mitt är skuret ett rektangulärt hål

Så tröghetsmomentet är mindre än den av en massiv cirkelskiva.

Du ska alltså inte addera.

Pieter Kuiper skrev:
pepsi1968 skrev:
Ur skivans mitt är skuret ett rektangulärt hål

Så tröghetsmomentet är mindre än den av en massiv cirkelskiva.

Du ska alltså inte addera.

Ok. det blir fortfrande fel med drygt 3 $k g m^{2}$ . Behöver man kompensera den stora cirkeln?

Tänk en hel cirkel minus rektangeln i mitten.

Tack hörni.. jag skrev arean av rektangeln som b+h istället för bh =)

Svara

Visa senaste svar