Måste ett "rum" vara en mängd med oändligt många element?

Rum är ingen helt precist definierad matematisk term, utan betyder bara ungefär "mängd med extra struktur". 

Exempel:

• Ett vektorrum är en mängd utrustad med en additionsoperation och en skalningoperation som uppfyller vissa kriterier.
• Ett normerat vektorrum är ett vektorrum som dessutom är utrustat med en norm (ett "storleksbegrepp") som uppfyller vissa kriterier.
• Ett metriskt rum är en mängd utrustad med en metrik (ett "avståndsbegrepp") som uppfyller vissa kritier.
• Ett topologiskt rum är en mängd utrustad med en topologi (ett "öppenhetsbegrepp") som uppfyller vissa kriterier.

Det finns ändliga exempel på alla de här typerna av rum.

Hehe utgår du från den där bilden?

Okej, kan du säga någon som har ändligt antal element, vilken som helst!

Exempel på ett ändligt vektorrum: Analogt med $\mathbb{R}^n$ och $\mathbb{C}^n$, så kan vi bilda vektorrummet $(\mathbb{F}_2)^n$, med komponentvis addition och skalning, över kroppen $\mathbb{F}_2=\{0,1\}$, som i sin tur är definierad utifrån följande additions- och multiplikationstabeller:

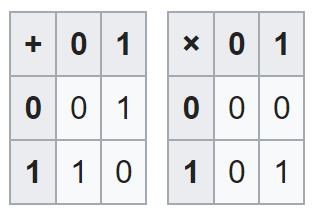
(Bild tagen från Wikipedia.)

Detta vektorrum innehåller $2^n$ stycken element, och är alltså helt klart ändligt.

Övning: Kolla upp axiomen för en kropp och verifiera $\mathbb{F}_2$ uppfyller dem. Kolla sedan upp axiomen för ett vektorrum och övertyga dig om att $(\mathbb{F}_2)^n$ uppfyller dem.

Exempel på ändligt metriskt rum: Som mängd tar vi återigen $(\mathbb{F}_2)^n$, men i stället för att utrusta den med addition och skalning så utrustar vi den med den så kallade Hamming-metriken, där man definierar avståndet mellan två $n$-tuplar som antalet komponenter där de skiljer sig åt.

Exempelvis är $d(\,{(1,0,0,0,1),\,(1,1,0,1,1)}\,)=2$ och $d(\,{(1,1,1,1,1),\,(0,0,0,0,0)}\,)=5$.

Fun fact: Hamming-metriken är en av grundbultarna i teorin för felrättande koder. En väldigt trevlig del av modern matematik som är väl värt att kolla upp någon gång när du får tid! ^_^

Övning: Kolla upp axiomen för ett metriskt rum, och övertyga dig om att $(\mathbb{F}_2)^n$ med Hamming-metriken uppfyller dem.

Världens tråkigaste exempel: Utgå från mängden $X=\{\mathbf{0}\}$.

Den kan betraktas som ett vektorrum över vilken kropp $\mathbb{F}$ som helst; definiera additionen som $\mathbf{0}+\mathbf{0}=\mathbf{0}$ och skalningen som $\lambda \mathbf{0}=\mathbf{0}$ för alla $\lambda\in\mathbb{F}$. Om vi vill kan vi även slänga på en norm genom att deklarera $\Vert \mathbf{0}\Vert=0$.

Vi kan också göra $X$ till ett metriskt rum genom säga att $d(\mathbf{0},\mathbf{0})=0$.

Eller så gör vi det till ett topologiskt rum genom att säga att $\varnothing$ och $\{\mathbf{0}\}$ utgör de öppna delmängderna av $X$.

Övning: Verifiera att det jag säger ovan stämmer genom att jämföra med axiomen för vektorrum, normerade vektorrum, metriska rum och topologiska rum.