Matematik 5000. Kurs 5. 3322 d)
Hej,
Vet inte hur man löser fråga 3322. Jag fattar inte.
Jag har hittat primitiv funktion men jag vet inte om jag ska ställa den = 1 eller om jag ska sätta in x=1 i funktionen eller.. något annat.

x och y får antas vara likformigt fördelade på respektive intervall.
Rita ett koordinatsystem och markera [0,π] på x-axeln och [0,1] på y axeln. Detta område är en rektangel med arean π.
Om vi tar a): "Arean under y=sin(x)" / "Totala arean (=π)" är den sökta sannolikheten.
b-d görs på liknande sätt.
Som e-uppgift och "bonus", studera
Tack.
Jo, jag har löst de andra. Ändå förstår jag inte den här. Jag tyckte det rimliga var att sätta in x = 1 för att få 2/3. Och sedan dividera med π för 2/3π.
Men svaret är något helt annat.
Dkcre skrev:Tack.
Jo, jag har löst de andra. Ändå förstår jag inte den här. Jag tyckte det rimliga var att sätta in x = 1 för att få 2/3. Och sedan dividera med π för 2/3π.
Men svaret är något helt annat.
Du har en graf "i rektangeln" enligt
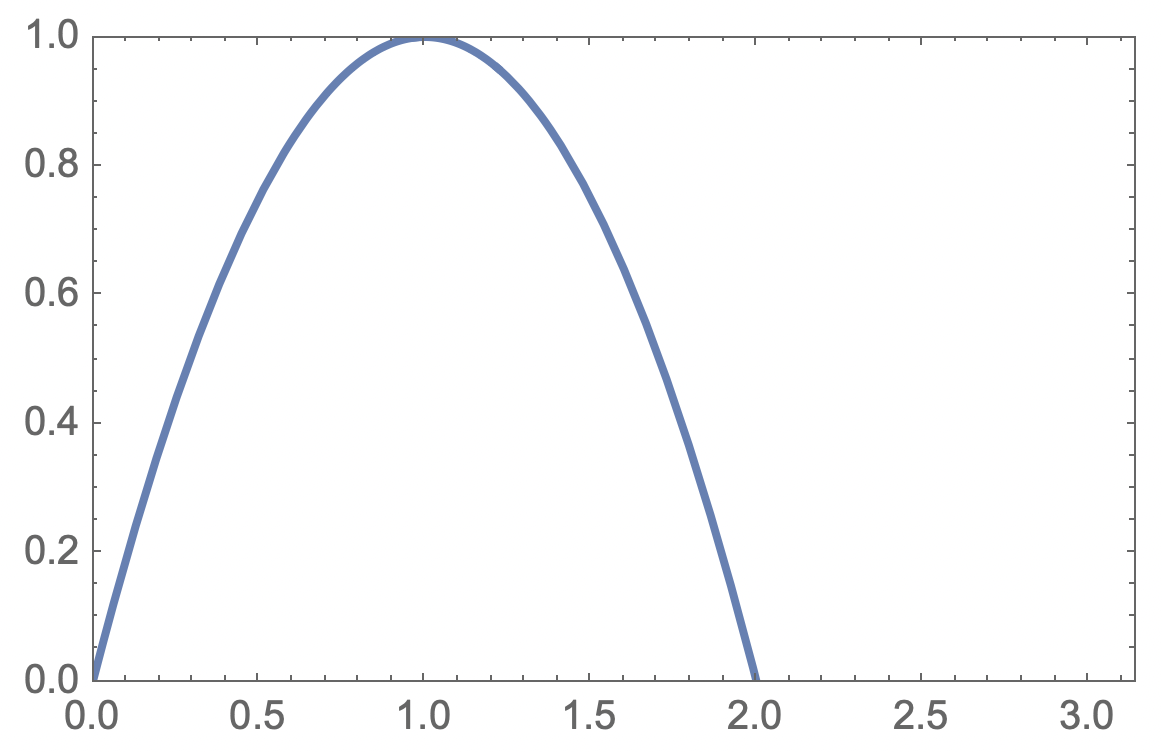
Du skall beräkna arean ovanför grafen, men inuti rektangeln. Sedan dividerar du den beräknade arean med rektangelarean π. Blir det inte rätt enligt facit?
Okej så du hittar skärningspunkterna först för 2x -x^2 = 0.
Sen vill jag hitta arean ovanför grafen, varför då? För det symboliserar området då y är större då?
Då sätter jag (π - 4/3)/π som blir rätt svar.
Men jag insåg inte dom första två stegen så då blir det svårt.
Dkcre skrev:Okej så du hittar skärningspunkterna först för 2x -x^2 = 0.
Sen vill jag hitta arean ovanför grafen, varför då? För det symboliserar området då y är större då?
Då sätter jag (π - 4/3)/π som blir rätt svar.
Men jag insåg inte dom första två stegen så då blir det svårt.
Ja, nollställena till grafen är 0 och 2.
Alla punkter (x,y) som ligger ovanför grafen, MEN INNANFÖR rektangeln uppfyller y>f(x). Dessa kallar vi "gynsamma punkter" och de har arean "π-arean under grafen". Notera att du får endast röra dig INOM rektangeln. INTE utanför. x och y är har begränsat definitionsintervall
π – "arean under grafen" blir som du skriver π – 4/3
Sedan har vi "Alla möjliga punkter" = rekangelarean = π
Du kommer säkert ihåg från sannolikhetsläran att vid likformig fördelning (som detta är) och via den klassiska sannolikhetsdefinitionen att vi har att
Sannolikheten = "Gynsamma utfall" / "Möjliga ufall"
vilket här blir "Gynnsamma punkter (area)" / "Möjliga punkter (area)".
Jag förstår. Tack för ditt svar.
Lika som vid kombinatoriken när man skulle räkna sannolikheten för olika händer i poker.
Dkcre skrev:Jag förstår. Tack för ditt svar.
Lika som vid kombinatoriken när man skulle räkna sannolikheten för olika händer i poker.
Exakt så !


