Matematik 5000. Kurs 5. 3359 b)

Man kan inte hitta en primitiv till $e^{-x^2}$ uttryckt i "vanliga" funktioner. Jag antar att du frågar detta för att du vill göra partiell integration? Testa istället variabelsubstitution, $t = x^2$. 

Förstår. Ganska.. irriterande fråga av boken då. Jag vet inte vad en variabelsubstitution är för något. Men jag har sett lite på professor Leonard emellanåt och han går igenom något som de kallar för "u-substitution" där man, typ, ändrar integralen genom att skriva om funktionerna på något sätt. Har att göra med att derivatan av x^2 är 2x i detta specifika fall då..

Jag har dock inte läst om det här själv eller satt mig in i det annars heller. Det tas inte upp i boken heller utan uppgiften kommer lite ifrån ingenstans.

Eventuellt om det togs upp i matte 4 och jag har glömt av det? Men amerikanerna verkar köra det i "calculus 2" (vad nu det är) så tror inte det...

Men jag läser om det och gör så.

Juste du har rätt, variabelsubstitution finns ej med i matte 5 (eller 4 för den delen). Jag ser inget direkt sätt att göra detta med hjälp av partiell integration. Detta är verkligen en klassisk "variabelsubstitution-integral". 

De kanske vill att man ska "se" att integrandet ser ut som kedjeregeln. Derivatan av $e^{-x^2}$ är $-2x e^{-x^2}$. Härifrån kan vi integrera båda led vilket ger att primitiv till $2xe^{-x^2}$ är $-e^{-x^2} + C$. Jag minns att det kunde finnas sådana frågor. 

Jag förstår inte. Får man skriva om en av funktionerna som ska integreras med sin derivata först, om du menar så? Är det alltid ok?

Eller jaha.. Ah, jag fattar. Irriterande.

Tack 

Det är bra absolut bra om man märker sådant eftersom det kan mycket snabbt leda fram till en lösning, men jag vet inte om man bör ha uppgifter med det som tänkt lösning. I alla fall inte i ett kapitel som är ganska irrelevant till sådana "knep" (jag antar att denna handlar om generaliserade integraler?). 

Ja, det är det jag menar. Syftet är att man ska lära sig hur man löser sådana, eller hur de fungerar och varför, inte hitta primitiva funktioner till knepiga integraler. Särskilt eftersom det var en av de svåraste jag sett i hela boken hittills. Men aja :p

Dkcre skrev:

Ja, det är det jag menar. Syftet är att man ska lära sig hur man löser sådana, eller hur de fungerar och varför, inte hitta primitiva funktioner till knepiga integraler. Särskilt eftersom det var en av de svåraste jag sett i hela boken hittills. Men aja :p

3359b går ut på att man skall se den inre derivatan av x^2 och kompensera för minustecknet.

Ingår inte var.sub. i Ma4 eller Ma5? Hm, jag minns ej om det var med på min tid.

Jo. Fast har aldrig löst en sådan förut utan bara sett det här. Fast det är väl ett bra test för att se om man är med på att det faktiskt är kedjeregeln man använder när man deriverar e^x..

Nej tror inte det. Det är också med i calculus 1 inte 2, och verkar vara ett ganska grundläggande koncept man lär sig tidigt i usa så vet inte varför vi valt att inte lära ut det tidigt. Fast kanske har fel nu då men tror inte det 

Nu har jag bara diff ekvationer kvar av den här kursen. Hoppas det är skoj.

Jag minns att någon annanstans i ma5 boken fanns en integral som ungefär såg ut $\displaystyle \int \frac{2x}{1+x^2}dx.$

Om man kan sina deriveringsregler inser man att täljaren är derivatan av nämnaren. Vidare gäller det, enligt kedjeregeln, att derivatan till $\ln(f(x))$ är $\frac{f^'(x)}{f(x)}$ (för en positiv deriverbar funktion $f$). Därmed blir integralen ovan $\ln(1+x^2) + C$. Att notera sådant här är ofta mycket användbart och trevligt! Exempelvis kan man snabbt få fram primitiv till $\tan x$ med denna ide.

Vill man ha sin dagliga dos av integraler finns

https://dailyintegral.com/

Dagens är (lätt version, det finns medium och svår också)

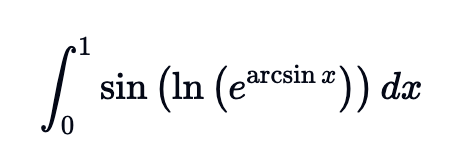
Såg denna webbsida för några veckor sedan. Ofta är det intressanta problem!

AlexMu skrev:

Såg denna webbsida för några veckor sedan. Ofta är det intressanta problem!

Bara det inte är för långtgående substitutioner...

Det här är ju en klassiker som i all sin enkelhet är jobbig

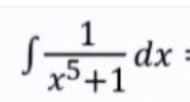
Finns det inte böcker med 100-tals integraler? Jag vill minnas jag sett någon för många år sedan.

Ja, det har hänt ibland. Generellt tycker jag att bestämda integraler är bättre på att inte vara jobbiga (det finns absolut en massa jobbiga sådana också), exempelvis med $\frac{1}{x^5+1}$ om man ska integrera på $[0, \infty)$ finns ju andra sätt att räkna den än att hitta primitiv. Så jag är glad att dailyintegral endast har bestämda! 

Och ja, det finns massvis med böcker fyllda med integraler. En jag läste förra året var "Inside Interesting Integrals". Den hade inte super många problem, men den gick igenom en massa integrationstekniker och sedan avslutade varje kapitel med några integraler att räkna på. Rätt trevlig för att lära sig fler integrationstekniker. 

Efter det har jag, on and off, gjort problem i boken "Almost Impossible Integrals, Sums and Series". Den innehåller 60 st integraler och 60 st serier att beräkna. Problemen är ofta coola och trevliga men det har även funnits problem med tyngre beräkningar beräkningar. Ett exempel är när författaren själv i sitt lösningsförslag använder mathematica: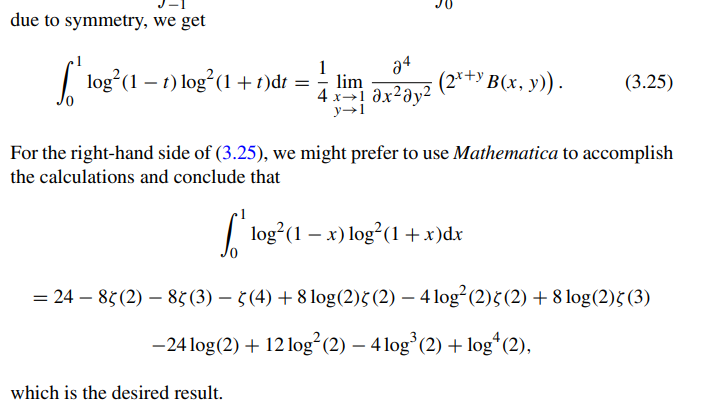 
Det är sant att högerledet är rätt jobbigt att räkna för hand och är generellt monotona beräkningar, men i så fall tycker jag att man kanske ska undvika att ha med sådana problem. 

Å andra sidan är det en användbar teknik att kunna skriva om integraler till något som kan lösas med "lätta beräkningar" och då kanske det är rättvist att låta en dator göra det. Jag var i alla fall lite sur när jag insåg att författaren tog en sådan genväg. 

AlexMu skrev:

Ja, det har hänt ibland. Generellt tycker jag att bestämda integraler är bättre på att inte vara jobbiga (det finns absolut en massa jobbiga sådana också), exempelvis med $\frac{1}{x^5+1}$ om man ska integrera på $[0, \infty)$ finns ju andra sätt att räkna den än att hitta primitiv. Så jag är glad att dailyintegral endast har bestämda! 

Och ja, det finns massvis med böcker fyllda med integraler. En jag läste förra året var "Inside Interesting Integrals". Den hade inte super många problem, men den gick igenom en massa integrationstekniker och sedan avslutade varje kapitel med några integraler att räkna på. Rätt trevlig för att lära sig fler integrationstekniker. 

Efter det har jag, on and off, gjort problem i boken "Almost Impossible Integrals, Sums and Series". Den innehåller 60 st integraler och 60 st serier att beräkna. Problemen är ofta coola och trevliga men det har även funnits problem med tyngre beräkningar beräkningar. Ett exempel är när författaren själv i sitt lösningsförslag använder mathematica: 
Det är sant att högerledet är rätt jobbigt att räkna för hand och är generellt monotona beräkningar, men i så fall tycker jag att man kanske ska undvika att ha med sådana problem. 

Å andra sidan är det en användbar teknik att kunna skriva om integraler till något som kan lösas med "lätta beräkningar" och då kanske det är rättvist att låta en dator göra det. Jag var i alla fall lite sur när jag insåg att författaren tog en sådan genväg. 

Likaså när man ser "lösningar" på Instagram m.m. där de kastar om summa/integral eller deriverar under integraltecknet utan verifiering att det är tillåtet. En stor mängd "lösare" älskar att åberopa Feynman's metod (var det verkligen hans?) bara för att "name drop".

Att lösa integraler är som att ösa vatten ur Atlanten. Det tar aldrig slut och svårighetsgraden kan läggas på en nivå som knäcker vem som helst.

Jag räknade många sådana förr, men idag räcker tiden inte till längre. Finns så mycket annat som skall hinnas med på 24 timmar.

Jag tror andra namn för Feynman's metod/trick är "Differentiation under the integral sign" eller "Leibniz integral rule". Feynman's trick eller liknande som namn verkar verkligen ha fått fäste.