Matematik 5000. Kurs 5. Första ordningen exempel.

Svårt att läsa på dator, men på mobil kan man zooma så där går det.

Var tar det stopp för dig?

Vad står det på sidan innan? Är du med på det som står där? (Jag gissar att de löser y' + y = 0 eller y ' - y = 0.)

De löser y'+ay = 0 där. Det är helt solklart.

Lite svårt att förklara, jag förstår ingenting av det som är under 3, jag kör inte fast någonstans utan jag begriper ingenting utav det. Det står bara: för att visa att svaret på frågan är "nej" så gör vi "någonting" och kan vi visa "någonting" så är det bra. Visar vi att z' = 0 då har vi visat någonting bra"..

Är det alltså punkt 3 som är oklar? Är 1 och 2 begripliga?

Vad de gör är väl helt tydligt (men säg till om det inte är det heller), men jag antar att du undrar varför de gör just dessa saker.

De undrar om det finns andra funktioner än Ce^-ax som är lösningar. Vi tar en funktion vilken som helst och vi kallar den u(x). Vi kan skriva den u(x) = u(x) * e^ax * e^-ax (eller hur?). Nu har vi alltså u(x) = z(x) * e^-ax och därmed z = u * e^ax. Om z är en konstant så har vi inga nya lösningar, och annars har vi det. Det betyder att derivatan av z är intressant. Så vi deriverar z med produktregeln och får e^ax(u' + au). Om nu u satisfierar vår ursprungliga ekvation så är u' + au = 0 och då är z' = 0 och därmed z en konstant.

Det fattas kanske tankesteg här, men jag vet inte vilka du behöver. Blev det klarare?

Hej Laguna,

Ja, punkt 3. Det andra är mycket enkelt.

Tack för din förklaring, men jag förstår tyvärr inte. Det är ganska långt ifrån är jag rädd. Får återkomma någon annan gång och se om jag är med på det då.

Om vi undrar om det finns funktioner som fungerar, varför väljer man då att skriva u(x) = u(x) × e^ax × e^-ax? Man vill veta om en godtycklig funktion är en lösning, men ändå väljer vi något specifikt. Menar man att kolla om det finns en annan funktion som fungerar men som ändå inkluderar exponentialfunktionen i alla fall? I så fall känns det konstigt att formulera det som att undersöker om någon annan funktion fungerar..

Varför gör vi substitutionen med Z? Varför inte bara låta det vara u(x) × e^ax? 

Varför kan man inte lika gärna välja att u(x) =x^4+2x-5/7? 

Vill man visa att om C ändras så gäller inte sambandet, alltså kan inte C vara en funktion utan en konstant? Men C ändras ju i och med att det multipliceras med en faktor från exponenten.. dock så beror det väl inte av X kanske.

För mig så känns det som att man bara slänger dit lite symboler godtyckligt och ändrar lite på dem och sen har man kommit fram till det man vill... 

Två små svar, men inte svar på allt:

Vi behöver inte z. Det ska gå utan den, och det blir bara en liten smula annorlunda.

Vi antar ingenting alls om u(x), så vi kommer att få samtliga lösningar till ekvationen.

Det man vill göra i 3 är att bevisa att det inte finns flera lösningar till diffekvationen

$y\text{'}+ay=0 \left(1\right)$

än

 $u\left(x\right)=C·e^{-ax} \left(2\right)$

där $C$ är en konstant (dvs derivatan av $C$ är noll).

Man vill alltså bevisa att alla andra funktioner av x som inte ser ut som (2), inte heller är en lösning till diffekvationen (1).

Det bevisar boken genom att hitta på en funktion

$u\left(x\right)=z\left(x\right)·e^{-ax}$

där z(x) skulle kunna vara precis vilken funktion av x som helst (dvs alla andra funktioner av x). Därefter visar man att z(x) isåfall måste vara en konstant. Och därmed har man visat att enda lösningen till (1) är (2).

Okej. 

Men så man multiplicerar Z(x) då med en lösning som redan är verifierad i det här fallet, och den lösningen, funktionen, fungerar i princip som en konstant här. Eller en referens.

Annars skulle det vara svårt att bevisa eftersom det finns oändligt med funktioner?

Så OM det fanns en annan lösning, så skulle derivatan av produkten av U(x) resultera i att den derivatan + den definierade funktionen u(x) resultera i 0. Och det kan endast inträffa om z(x) är en konstant, annars är det förhållandet omöjligt? 

Så man använder en verifierad lösning och letar efter en motsägelse till den lösningen...? Typ..

JohanF skrev:

Det man vill göra i 3 är att bevisa att det inte finns flera lösningar till diffekvationen

$y\text{'}+ay=0 \left(1\right)$

än

 $u\left(x\right)=C·e^{-ax} \left(2\right)$

där $C$ är en konstant (dvs derivatan av $C$ är noll).

Man vill alltså bevisa att alla andra funktioner av x som inte ser ut som (2), inte heller är en lösning till diffekvationen (1).

Det bevisar boken genom att hitta på en funktion

$u\left(x\right)=z\left(x\right)·e^{-ax}$

där z(x) skulle kunna vara precis vilken funktion av x som helst (dvs alla andra funktioner av x). Därefter visar man att z(x) isåfall måste vara en konstant. Och därmed har man visat att enda lösningen till (1) är (2).

Jag tror(!) att Dkcre:s huvudfråga är varför man ansätter just denna formen

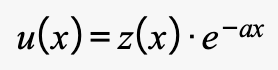
Vad är motiveringen till just denna form, och varför inte "e^(-a x u(x))" eller någon annan avart?

Om vi bortser från separation av variabler och bara fokuserar på bokens (många böckers, inkl. H GASK) ansats så tror jag detta kräver en grundlig motivering för att ge ett bra bevis.

Stämmer!

Jo, precis! Vad jag tror boken vill göra, är att "göra det lite troligare" för läsaren att det inte finns andra lösningar än den man har hittat. Med hjälp av gymnasiematematik. Anledningen till att boken har ansatt den lösning man har ansatt, är att det är relativt straight forward att visa att det inte finns just sådana lösningar eftersom man behöver ju då bara visa att derivatan av z måste vara lika med noll.

Att _fullständigt_ bevisa att det inte finns andra lösningar ligger nog på en _helt_ annan matematisk nivå. Jag vill minnas att man inte ens gick igenom sådana fullständiga bevis på fortsättningskurser i diffekvationer på högskolan. (...och jag gick runt på Chalmers med precis samma fundering som du, Dkcre!)

JohanF skrev:

Jo, precis! Vad jag tror boken vill göra, är att "göra det lite troligare" för läsaren att det inte finns andra lösningar än den man har hittat. Med hjälp av gymnasiematematik. Anledningen till att boken har ansatt den lösning man har ansatt, är att det är relativt straight forward att visa att det inte finns just sådana lösningar eftersom man behöver ju då bara visa att derivatan av z måste vara lika med noll.

Att _fullständigt_ bevisa att det inte finns andra lösningar ligger nog på en _helt_ annan matematisk nivå. Jag vill minnas att man inte ens gick igenom sådana fullständiga bevis på fortsättningskurser i diffekvationer på högskolan. (...och jag gick runt med precis samma fundering som du, Dkcre!)

Detta är nog "pudelns kärna". Här får nog LuMa07 gripa in som lite mera insatt än undertecknad. Men jag skulle tro att e^(-ax) är en (funktions)lösningsbas och det därmed endast känns "meningsfullt" att ansätta en multipel av denna bas. Frågan är vad som säger att detta är den enda basen. Det vore intressant att se något mera strikt resonemang.