Matematik 5000. Kurs 5. Uppgift 3221. Nollställe.
Hej
Fråga 3221 d)
Hur löser man den? Mitt svar är att jag vet inte.
Tänker att man inte kan veta om f(x) skär x axeln eller inte, men har sett facit så vet att de är fel.
F(x) kan tydligen ha en,två eller tre nollställen beroende på värdet vid f(2) och f(4), står det. Säger mig ingenting.

För det första måste vi begränsa vårt uttalande till visat intervall [1,5]. Om du skulle skissa kurvan, m.h.a. information för y=f'(x) hur skulle den se ut? Rita INTE ut några koordinataxlar, utan bara skissa kurvan på ett blankt papper.
Trinity2 skrev:För det första måste vi begränsa vårt uttalande till visat intervall [1,5]. Om du skulle skissa kurvan, m.h.a. information för y=f'(x) hur skulle den se ut? Rita INTE ut några koordinataxlar, utan bara skissa kurvan på ett blankt papper.
Jag tror något liknande det här:

Bra!
För olika värde i konstant-termen i funktionen för flyttas grafen i vertikalt led upp och ner, vilket innebär att den placeras på olika "höjder" relativt x-axeln. Om du skulle placera x-axeln i bilden ovan på olika ställen, hur många lösningar till ekvationen f(x)=0 får du då?
Placera in x-axeln och visa vilka fall du kommer fram till.
Ah.
Jag förstår.
Och om man inte har specat ett särskilt intervall som ju i sådant fall skulle "kapa av" båda benen på grafen, så kommer den oundvikligen någon gång att skära X i något "ben" eller ände.
Därför är absoluta minimum 1 nollställe.
Dkcre skrev:Ah.
Jag förstår.
Och om man inte har specat ett särskilt intervall som ju i sådant fall skulle "kapa av" båda benen på grafen, så kommer den oundvikligen någon gång att skära X i något "ben" eller ände.
Därför är absoluta minimum 1 nollställe.
Ja... och nej.
Ja: Här får vi tolka grafen i boken som att den fortsätter oändligt högt upp utanför figuren för alla x. Då stämmer det att f(x) alltid har minst ett nollställen. Det är nog den tolkningen man SKALL göra.
Om man bara tolkar det man ser, så skulle vi t.ex. kunna ANTA att f'(x) är en parabel med f'(x)=2 (x - 3)^2 - 2 = 2 x^2-12 x+16 vilket skulle ge
f(x) = (2 x^3)/3-6 x^2+16 x + C
där olika C skulle ge olika kurvor;
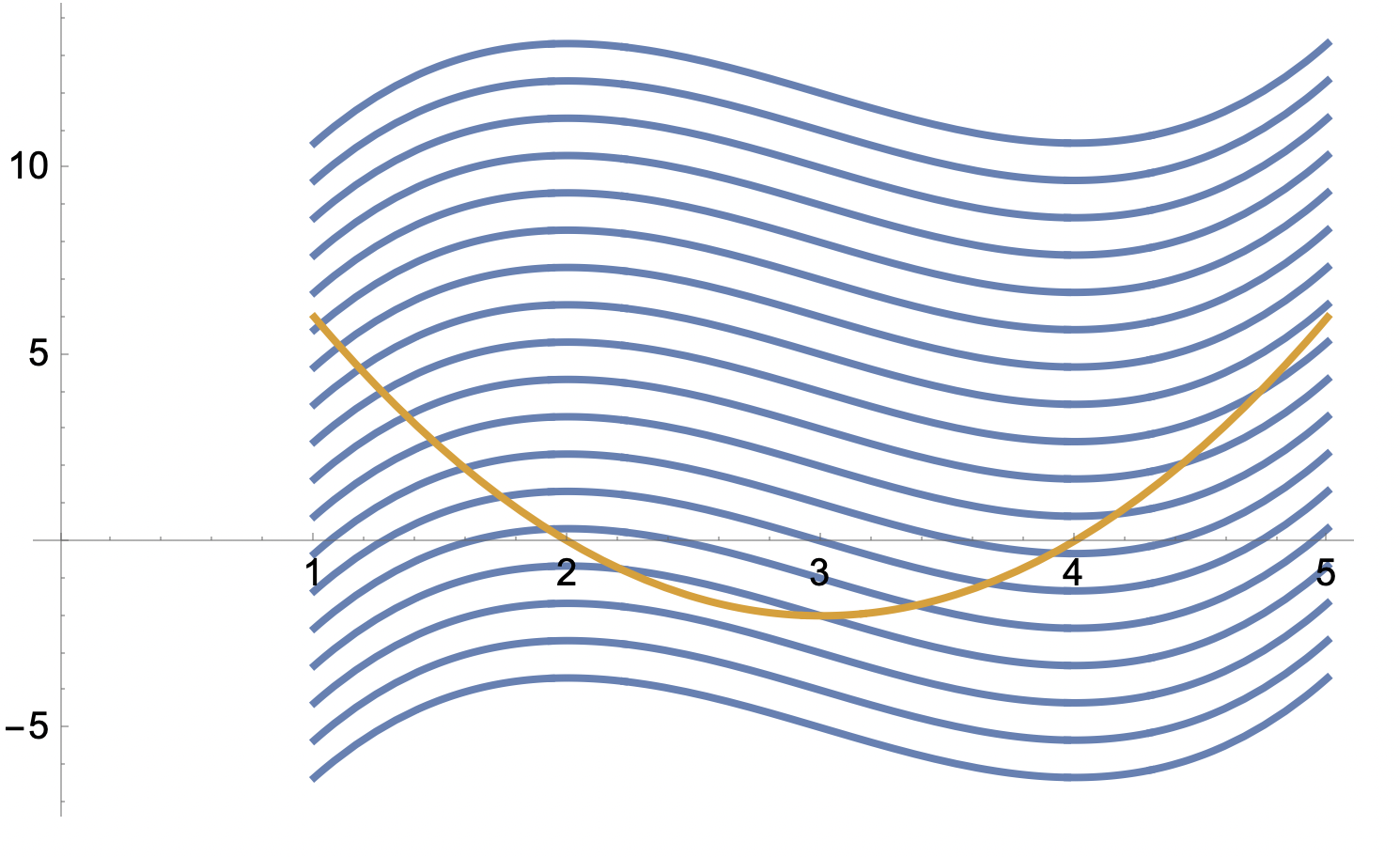
Här är det inte självklart att f(x) har något nollställe. Notera att vissa kurvor skär ej x-axeln.
Detta är dock troligen INTE den tolkning man skall göra av grafen i boken.
Det Trinity2 skriver stämmer om vi antar att definitionsmängden för f(x) är begränsad.
För obegränsade definitionsmängder gäller det istället att alla tredjegradsfunktioner alltid har minst ett nollställe.
Yngve skrev:Det Trinity2 skriver stämmer om vi antar att definitionsmängden för f(x) är begränsad.
För obegränsade definitionsmängder gäller det istället att alla tredjegradsfunktioner alltid har minst ett nollställe.
Problemet här - som jag ser det - är att vi inte vet något om karaktären på f'(x). Kanske det är ett polynom av grad 2, men det är inte säkert. Även om D_f är obegränsad behöver det inte innebära att f är det. y=f(x) kan t.ex. vända nedåt för x<-1 och x>8 och plana ut i en horisontell asymptot och då är det inte svårt att parallellförflytta grafen så att den saknar nollställen. Uppgiften är dåligt formulerad och fri för tolkning.
Tack 👌
Förstår invändningen.



