Matematik 5000. Kurs 5. Uppgift 3223
Ser jag inte den lätta lösningen? Jag får för Ma5 alltför omfattande räkningar. Finns en snabb och elegant metod lämpad för kursen?
Äh, läste fel två gånger.
Kan tanken vara att den ska lösas med digitala hjälpmedel?
y' får vi rätt lätt. I den kan vi kalla e-0,6x för z, och då har vi ungefär -z/(a+z)2 (jag använde generella konstanter när jag kladdade). Vi ska maximera detta, och det är samma som att maximera (a+z)2/z (med vetskapen att z inte kan vara negativ).
Laguna skrev:y' får vi rätt lätt. I den kan vi kalla e-0,6x för z, och då har vi ungefär -z/(a+z)2 (jag använde generella konstanter när jag kladdade). Vi ska maximera detta, och det är samma som att maximera (a+z)2/z (med vetskapen att z inte kan vara negativ).
Det var min första tanke också, men det är lurigare än så då denna graf inte har ett maximum
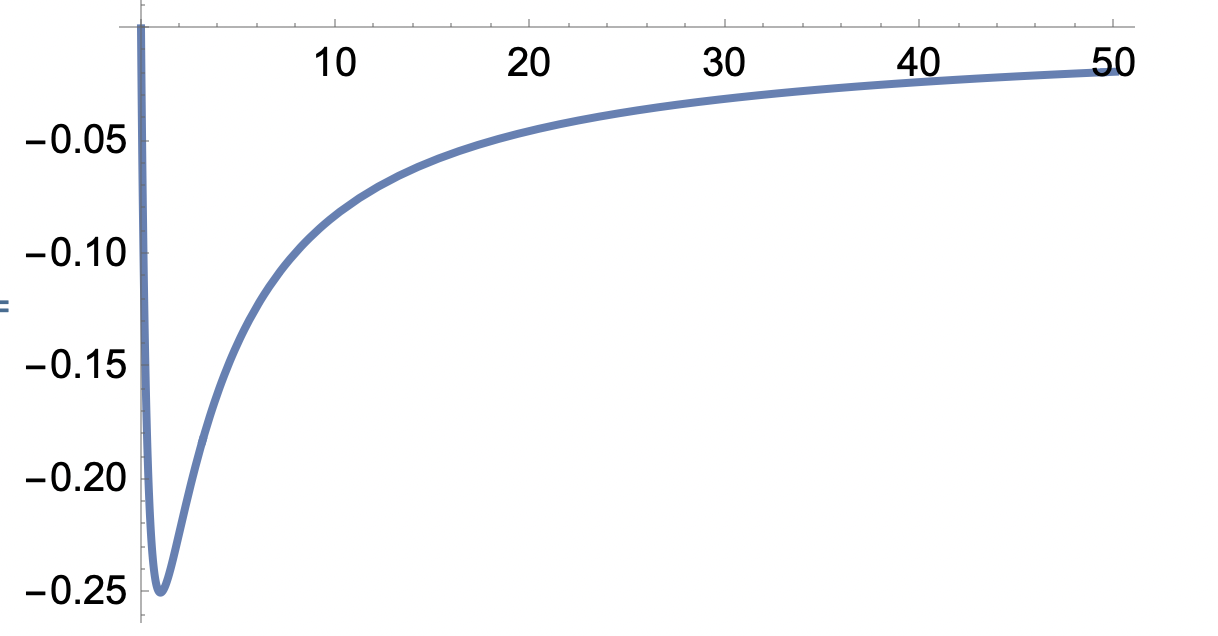
Jag skall renskriva min lösning så får vi se om det är den rekommenderade.
Yngve: Jag trodde först samma sak, men "3223" har ingen ruta.
Laguna skrev:y' får vi rätt lätt. I den kan vi kalla e-0,6x för z, och då har vi ungefär -z/(a+z)2 (jag använde generella konstanter när jag kladdade). Vi ska maximera detta, och det är samma som att maximera (a+z)2/z (med vetskapen att z inte kan vara negativ).
Är detta avsedd lösning? Känns lite "mycket" för en vanlig uppgift
Detta är nog inte omöjligt för ma5 nej.
I kursen Matematik 5 används den logistiska funktionen för att modellera tillväxt som har en övre begränsning, till exempel hur en population växer i ett område med begränsade resurser.
Funktionen dyker upp under differentialekvationer av typen y'=ky(M-y). M=övre gränsen för tillväxten. Funktionen y har en s-form och har sin största tillväxt i inflexionspunkten, vilket ligger på y=M/2. I det här talet på 75/2=37,5.
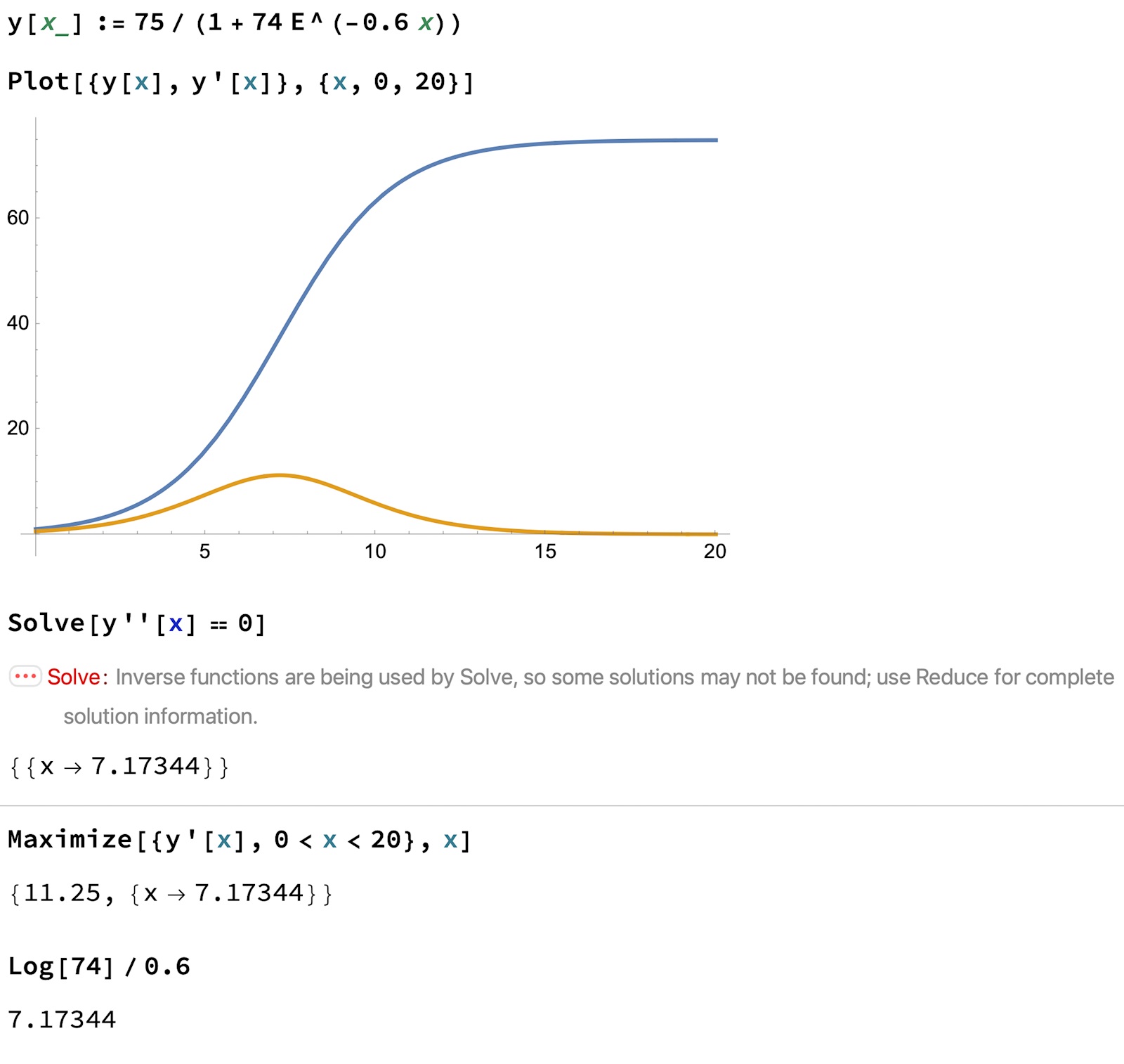
visar att min uträkning är rätt.
MrPotatohead skrev:Detta är nog inte omöjligt för ma5 nej.
Tack! Jag har inte boken så jag vet inte vilken nivå de ligger på.
