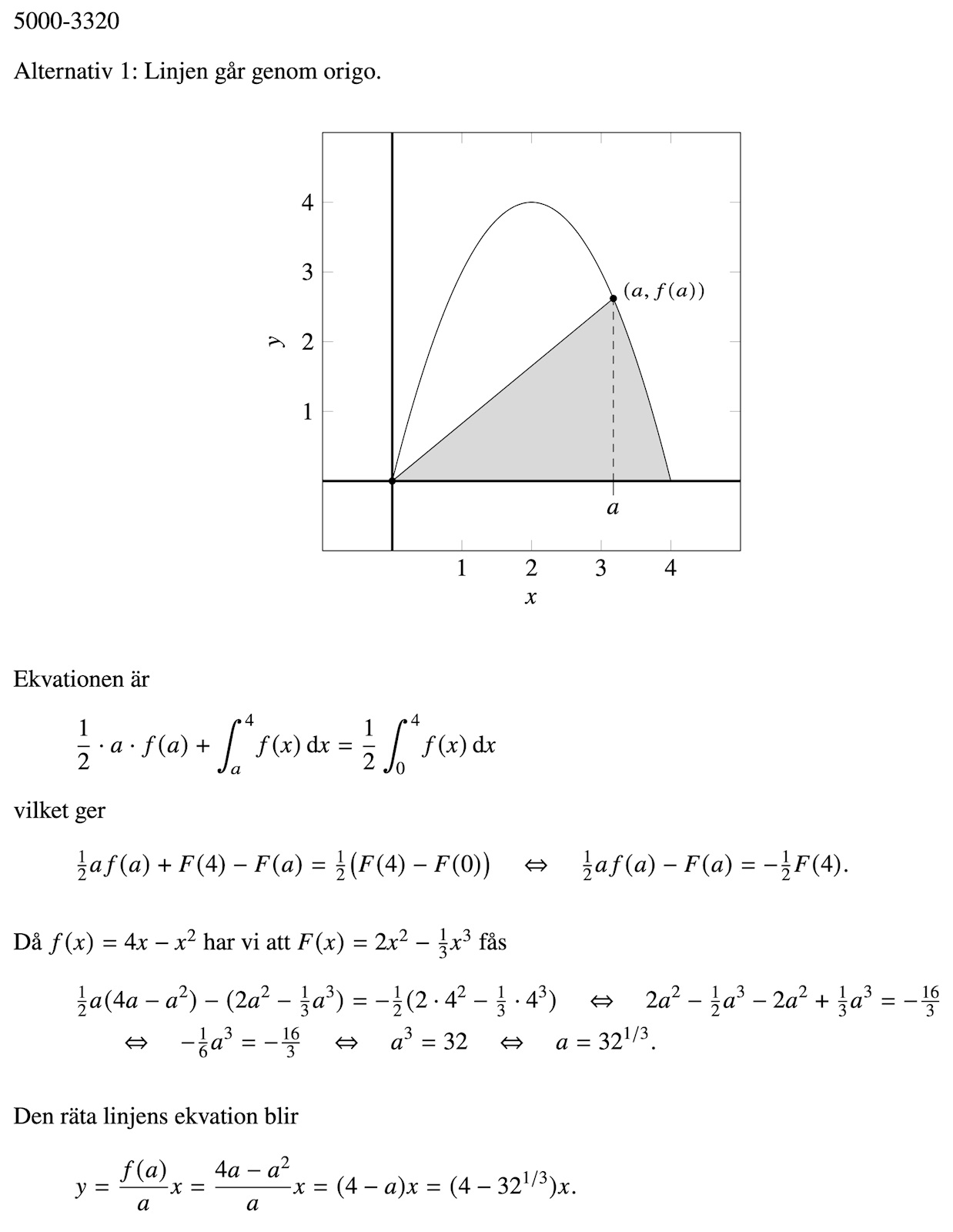
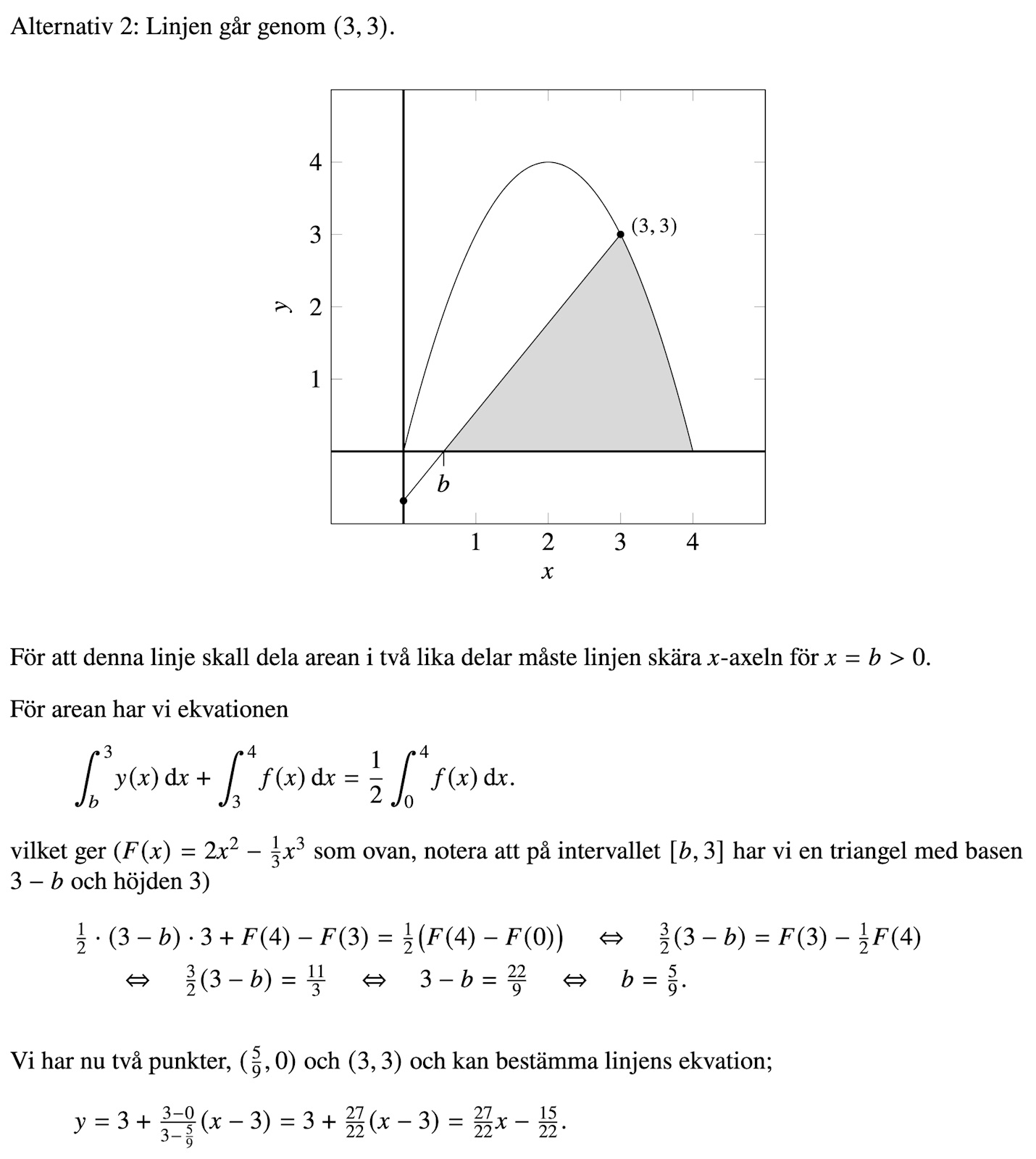
Matematik 5000. Kurs 5. Uppgift 3320.
Hej!
På fråga 3320 är rötterna till funktionen 4 och 0.
Jag har integrerat och räknat ut att halva arean är = 32/6.
Jag har sedan valt en punkt på grafen, nämligen (3,3) och satt funktionen för linjen till y = kx + m och för ena punkten då 3 = k3 + m.
Eller vänta, punkten måste ju faktiskt också ligga på grafen! XD det glömde jag
Sen har jag ingen aning.

Det är en rätt bra början, men en sak som krånglar till det lite är att vi inte vet om den linjens andra skärningspunkt med området är på x-axeln eller y-axeln, så vi vet inte hur ett integraluttryck för arean ser ut, så att vi kan få en ekvation till för k och m.
Jag föreslår linjen y = kx i stället.
Vi kan köra färdigt med ditt val sedan, det ska inte vara omöjligt, men då behöver jag rita lite också.
Arean under en rät linje mellan (0,0) och (3,3) > halva arean så det är ine möjligt att välja en punkt på linjen där arean delas i två lika stora delar.
Det blir enklare att välja (0,0) som fix punkt med linjen y=kx som Laguna skriver.
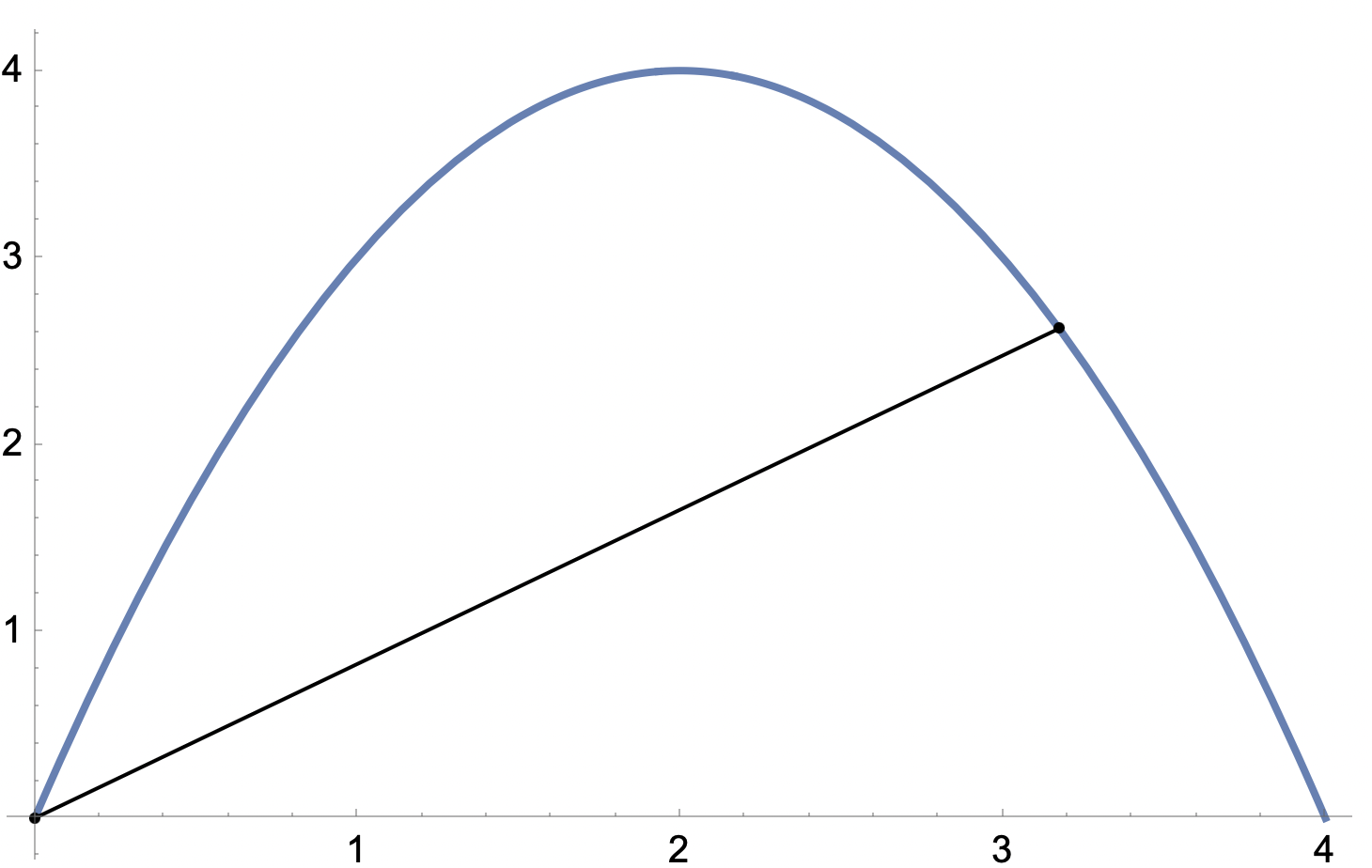
Förstår. Ja, jag har kluddat ner vad jag begriper här..
Ja, a ska ersättas med x istället.
Eller nedan bild blir helt fel kom jag på, dessutom är F(x) felskriven osv..
Uttrycket borde bli (2x^(2) -(x(^3))/3) - ((x(2x^(2)-(x^(3))/3))/2 = 32/6

Det här verkar inte vara lätt. Får man använda digitala hjälpmedel?
Kanske inte. Eller så är det väldigt lätt egentligen.. men hamnar man inte i rätt tanke från början..
Har gett det några timmar nu och jag grejar det inte. Gick vidare och tar lättare uppgifter så länge.
Ingenting tyder på att det är tillåtet i alla fall. Egentligen åt andra hållet också för den delen.
Här är facits lösningar:

Den undre kom jag också fram till, men jag trodde båda punkterna skulle ligga på grafen, men det är nog en för snäv tolkning. Skall kolla på det andra alternativet nu.
Snyggt :)
Svår uppgift. Jag tycker Dkcre kom ganska långt.