Matematik 5000. Kurs 5. Uppgift 3323 a,b,c
Hej,
Jag vet inte hur man ska göra helt enkelt.
Enligt facit så letar jag efter när värdet under rottecknet i pq formeln blir icke negativt. Så man får väl lista ut ett sätt att hitta ett förhållande mellan p & q där det här inte inträffar till att börja med.
Hade aldrig på egen hand kommit fram till steg 0 på uppgiften vilket känns drygt men ok.

Dkcre skrev:Hej,
Jag vet inte hur man ska göra helt enkelt.
Detta är en variant av 3322 men du har inte fått "relationen" på förhand.
Du måste nu ställa upp relationen mellan p och q för att det skall bli reella rötter. Kommer du ihåg diskriminanten?
När du väl har funnet detta samband mellan p och q är detta ungefär som 3322d.
I deluppgifterna a-c varierar dock definitionsintervallet och det gäller att se hur din graf faller inom dessa 3 kvadrater.
Rita! A och O här är att rita och tänka "vilken area är intressant", "Vilka punkter är gynnsamma", etc.
Jag brukar ha svårt för att komma fram till hur man ens ska göra så jag kan inte börja på uppgifterna ens. Resten är lättare. Fast det gäller förvisso alla problem man ska lösa ^^'
Är 1 och 2 rätt? Fast jag vet inte.. det är ju inte riktigt korrekt nu när jag skriver det här för= 0 är väl en dubbelrot kom jag på. Så det kanske räcker med >< tecken. Som nu är tillagt..
Bilden avser alltså när D blir negativ..

Det ser bra ut. För att vi skall få reella rötter måste D≥0 Jag kallar ditt Q för D, då du har q senare och "D" är lite snyggare och påminner om ordet "Diskriminanten"
D=p^2/4-q
D≥0
p^2/4-q≥0
q≤p^2/4
För att nu inte röra till det i huvudet byter vi till något mera "hemma",
y ≤ x^2/4
Kan du nu göra uppgift a). Det tror jag.
Det blev då såhär.
Fast nu dividerar man ju inte med ett område, eller med möjliga utfall. Eller är det området 1 i det här fallet eftersom både p och q kan hamna inom 0-1 då..
Så jag skulle ha dividerat med 1

Dkcre skrev:Det blev då såhär.
Rita en vacker bild för mig på definitionsområdet, grafen, gynnsamma punker och möjliga punkter.
Du tänker rätt, men skriver kort...
Trinity2 skrev:Dkcre skrev:Det blev då såhär.
Rita en vacker bild för mig på definitionsområdet, grafen, gynnsamma punker och möjliga punkter.
Du tänker rätt, men skriver kort...
Såhär tänker jag att det ser ut. Fast nu har jag ritat grafen efter primitiva funktionen, det skulle ha varit derivatan.

Dkcre skrev:Trinity2 skrev:Dkcre skrev:Det blev då såhär.
Rita en vacker bild för mig på definitionsområdet, grafen, gynnsamma punker och möjliga punkter.
Du tänker rätt, men skriver kort...
Såhär tänker jag att det ser ut.
Mycket fint! Glöm inte att "Möjliga utfall" är inte "bara" det vita, utan HELA kvadratens area.
Vad blir nu slh?
Tänk på vad q^2/4 blir för q=1, Det blir 0.24 så lite mera över 0.1 som du har ritat
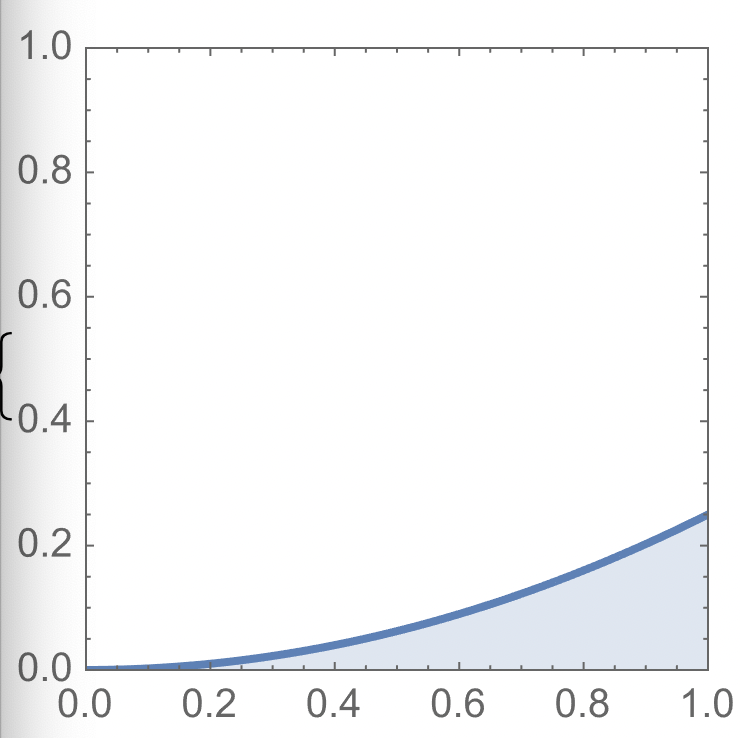
Ja, jag råkade rita den primitiva funktionen för def mängden och inte derivatan, såg felet när jag skulle posta.
Jag tänker fortfarande då att det är (1/12)/1.
B och c är triviala. (Gjorde b lite snabbt och blev rätt)
Tycker det är så svårt. Tack för att du hjälper mig.
Jag upplever det i varje fall som att jag förstår uppgiften väl nu :)
Dkcre skrev:Ja, jag råkade rita den primitiva funktionen för def mängden och inte derivatan, såg felet när jag skulle posta.
Jag tänker fortfarande då att det är (1/12)/1.
B och c är triviala.
Tycker det är så svårt. Tack för att du hjälper mig.
Jag upplever det i varje fall som att jag förstår uppgiften väl nu :)
Bra! Ja. det är rätt med (1/12)/1.
I b) och c) förstoras kvadraten och då även "gynnsamma området". Du gör precis på samma sätt.
Vi som sitter här tycker bara det är kul med elever och frågor! Jag talar iaf för mig själv...


