Matematik 5000. Kurs 5. Uppgift 4241
Hej
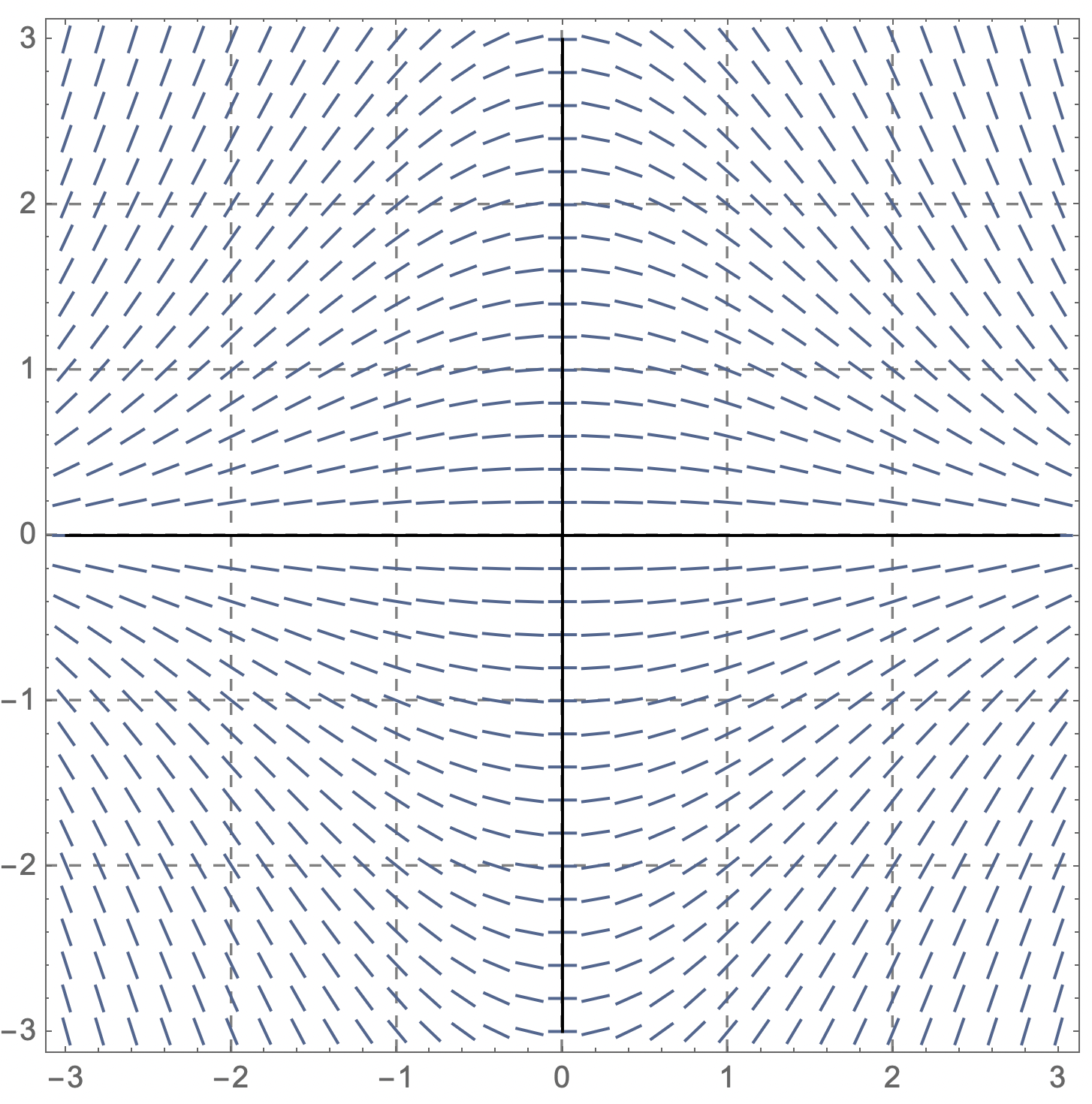
"Vilket riktningsfält svarar mot diffekvationen y' = -0.4xy?"
Tänker att man då.. ehm.. först tänker ut vad funktionen måste vara då och sedan plottar ut punkter och kontrollerar om riktningspilen verkar luta ungefär enligt ekvationen där. Problemet är att jag vet inte hur man löser ekvationen
Om jag minns rätt så visar riktningsfältet derivatan i massvis av olika punkter för att ge en ide av hur lösningsfunktionen ser ut. Ett sätt att lösa uppgiften är då att beräkna lutningen i några olika punkter och se vilka riktningsfält som stämmer överens med ens resultat. T.ex om du stoppar in punkten (1, 1) så får du att y' är y' = -0,4(1)(1) = -0,4. I punkten (1, 1) bör lutningen på pilen vara -0,4. Så man får prova lite olika värden.
Lite arbetssamt om man skall göra det för hand. Geogebra? Lär finnas Pythonprogram för miniräknare.
Några små synpunkter:
- Man kan vara systematisk för att få ner arbetet, t ex genom att välja ett par y-nivåer och sen sätta in ett antal x-värden. Det räcker med positiva x för det blir samma värde men omvänt tecken för negativa. Man ser också att för negativa y-värden byter y´ tecken så då blir det
en upp-och nervänd kurvskara.
- Man kan ha på känn att en exponentialfunktion (y´= - nånting y) spökar. En inre funktion x2 ger ju ett x för inre derivatan. Lösningen blir y= A e- 0,2 x^2 (Gauss´ "klockkurva")


