Matematik och Fysikprovet - Matte 2017 fr. 26

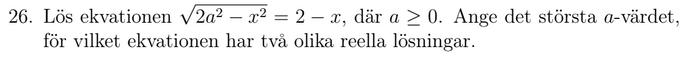
Låt mig visa hur långt jag har kommit. Först med respekt till VL måste $2 a^{2} - x^{2} \geq 0$ stämma även när vi ändrar på ekvationen.

Sedan skriver jag om ekvationen i form $a x^{2} + b x + c$ så att jag kan se till att diskriminanten är större än noll.

$\sqrt{2 a^{2} - x^{2}} = 2 - x 2 a^{2} - x^{2} = 4 - 4 x + x^{2} 2 x^{2} - 4 x + 4 - 2 a^{2} = 0 x^{2} - 2 x + 2 - a^{2} = 0$

Dvs. att $b^{2} - 4 a c$ måste vara större än noll. Det är antingen när $2 - a^{2} \leq 0$ dvs. $a \geq \sqrt{2}$ eller:

$b^{2} - 4 a c > 0 4 - 4 (1) (2 - a^{2}) > 0 4 a^{2} > 4 | a | > 1$

Men för att frågan säger $a \geq 0$ betyder det att $a > 1$ eller $a \geq \sqrt{2}$ .

Om man återvänder till kontrollen man etablerade i början $2 a^{2} - x^{2} \geq 0$ kommer man fram till att $a \geq \frac{x}{\sqrt{2}}$ .

Jag listade ut det själv. Någon moderator får gärna ta bort inlägget eller låta det vara för framtiden.

alexanderstroborg skrev:
Jag listade ut det själv. Någon moderator får gärna ta bort inlägget eller låta det vara för framtiden.

Kommer du ihåg hur du gjorde haha?

Svara