Matematisk analys i flervariabel

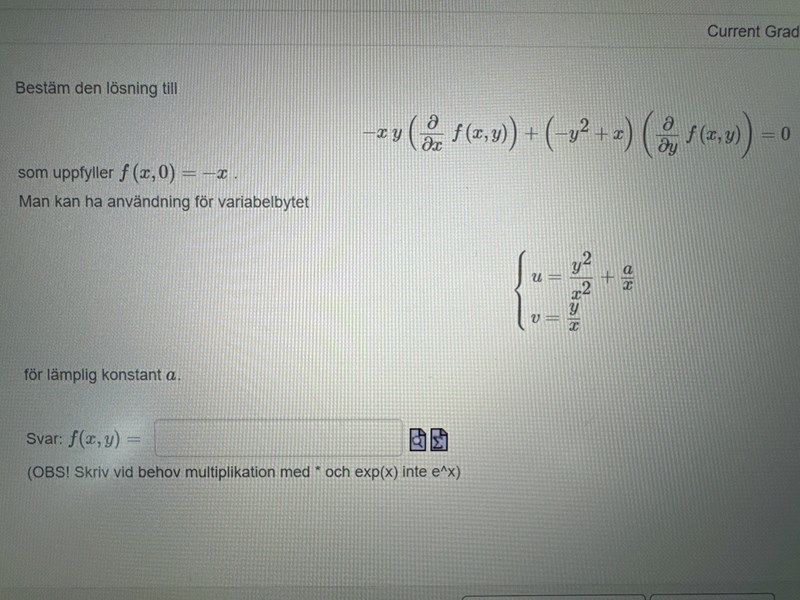
Du har kommit fram till rätt konstant $a$, men jag förstår inte riktigt vad du gjort. Det kan hända att $g_1$ och $g_2$ är derivator av $u$ respektive $v$, men det är inkonsekvent.

Skriv om differentialekvationen med $u$ och $v$. Tänk på att

$\displaystyle \frac{\partial f\left(u(x,y),v(x,y)\right)}{\partial x}=\frac{\partial f}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial x}$

Samma sak gäller såklart när man partialderiverar med avseende på $y$. När du skrivit om ekvationen och satt in konkreta uttryck för partialderivatorna ser man att flera termer försvinner och kvar blir ett ganska enkelt uttryck, särskilt om man väljer $a=-2$.

Utnyttja slutligen att $f(x,0)=-x$, vad betyder det om man har en funktion $f(u,v)$ och hur ska man hantera det? Finns det någon genväg?

Jag förstår inte riktigt vad du menar, efter att jag har fått a=-2 och sätter in den i ekvationen så får jag g1=0 och på samma sätt mst jag få g2 att bli noll men jag förstår inte vad nästa steget är.

Om $\frac{\partial f\left(u,v\right)}{\partial v}=0$ så är

$f(u,v)=C_1+h(u)$

För någon konstant $C_1$ och någon funktion som beror av variabeln $u$.

Dessutom ska du om du återgår till $x,y$ också ha $f(x,0)=-x$

ja precis om vi pratar i termer av g1 och g2 så fick jag att 1*g2=0 där g2 är derivtan av v map x och y, men jag får det till=0 så jag förstår inte riktigt hur jag ska hitta primitiva funktionen och sedan c.

Först och främst, om vi deriverar får vi (du får gärna byta ut derivatorna mot $g_1$ osv)

$-(xy)\left(\frac{\partial f}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial x}\right)+(-y^2+x)\left( \frac{\partial f}{\partial u}\frac{\partial u}{\partial y}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial y} \right)$

Vi sätter in de konkreta partiella derivatorna och förenklar

$v(a+2)\frac{\partial f}{\partial u}+\frac{\partial f}{\partial v}=0$

Väljer vi $a=-2$ får vi slutligen ekvationen

$\frac{\partial f}{\partial v}=0$

Med lösningarna

$f=C_1+h(u)$

Vidare har vi att $f(x,0)=-x$ och för $y=0$ är $u=-\frac{2}{x}$

Hur kan vi skapa en funktion $h(u)$ med detta relativt enkla $u$ som ger oss -x?