Matematisk ekvation

Jag ser inte riktigt vad det som står ovanför har med saken att göra, men på differentialekvationen skulle jag tänka så här:

Differentialekvationen:

$e^{x+2y}+y'=0$

är separabel, det kan bara vara lite svårt att se det. Om jag börjar så här:

$e^{x+2y}+y'=0$

$e^{x+2y}=-y'$

$e^x\cdot e^{2y}=-y'$

Ser du då hur du kan lösa den som en separabel differentialekvation?

Tack för ditt svar. Men jag förstår inte hur jag ska gå vidare med den?

AlvinB skrev:

Ser du då hur du kan lösa den som en separabel differentialekvation?

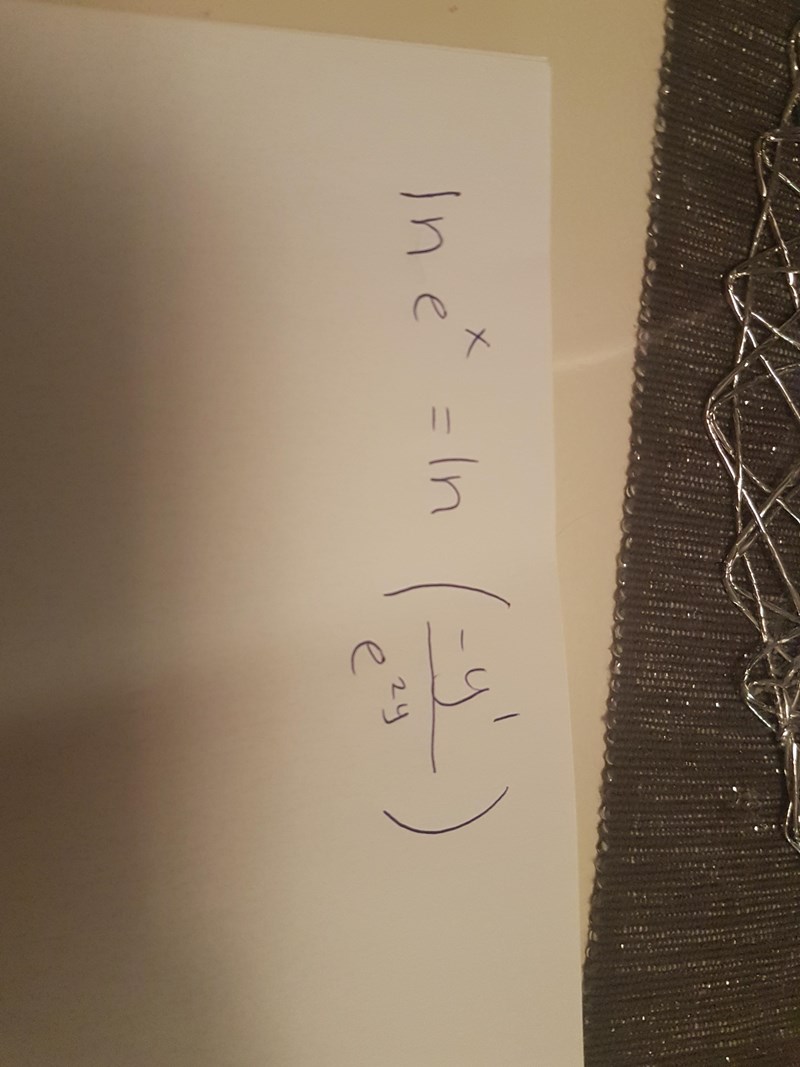får det till såhär? :(

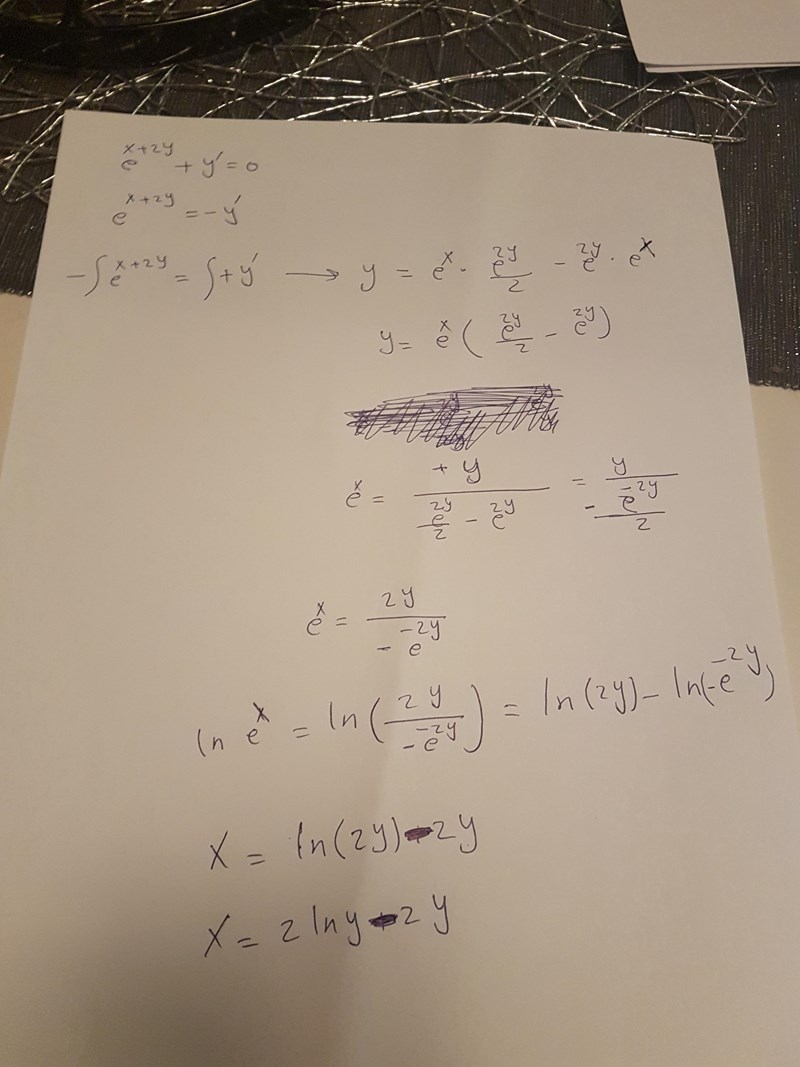kan någon rätta mig? Har jag tänkt rätt nu?

Snälla Lenajohansson, se till att dina bilder är rättvända innan du postar dem! Just nu får vi sitta såhär för att läsa dina inlägg:

Nja, det har blivit lite fel.

Du är väl bekant med metoden om separabla differentialekvationer?

Om vi får över allt innehållande $y$ på ena sidan och allt med $x$ på andra kan vi integrera båda led med avseende på respektive variabel.

$e^x\cdot e^{2y}=-y'$

$e^x=-\dfrac{y'}{e^{2y}}$

$e^x=-y'\cdot e^{-2y}$

$\displaystyle\int e^x\ dx=\int-e^{-2y}\ dy$

Fixar du resten själv?

Hos mig ser bilderna rättvända ut, vet inte hur jag ska göra annars.

Kan ni kolla om jag har löst det rätt nu?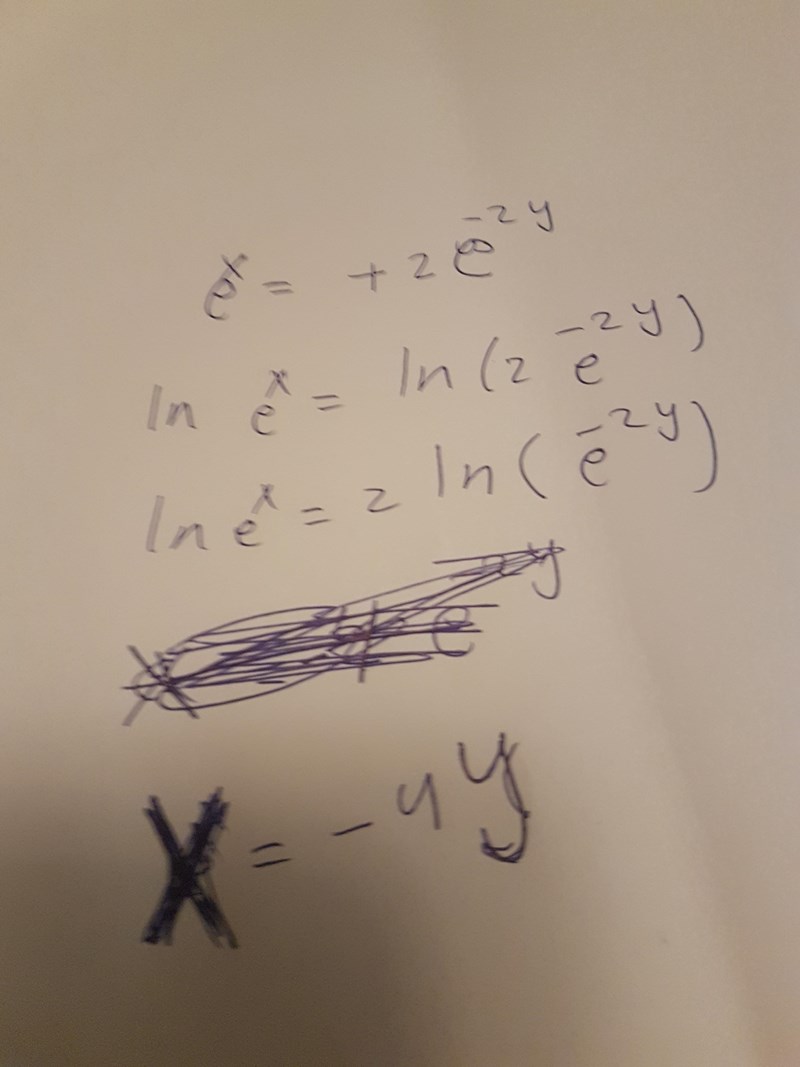

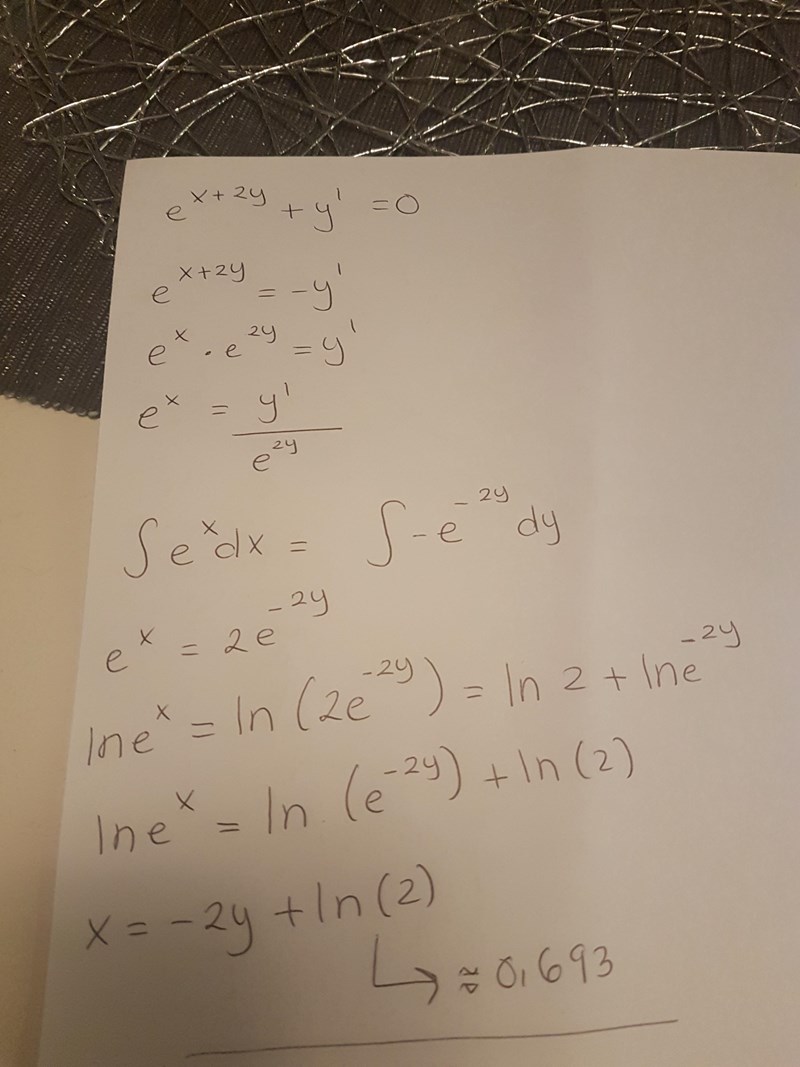tror jag tänkte fel ovan, detta känns mer rätt. Vad tycker ni?

För mig är bild nummer två vriden, och de andra rätt.

Vad får du om du deriverar $2e^{-2y}$?