Matematisk induktion och formel för summa

Det verkar som att frågan inte är bifogad!

Nu så:)

Enligt ChatGPT:

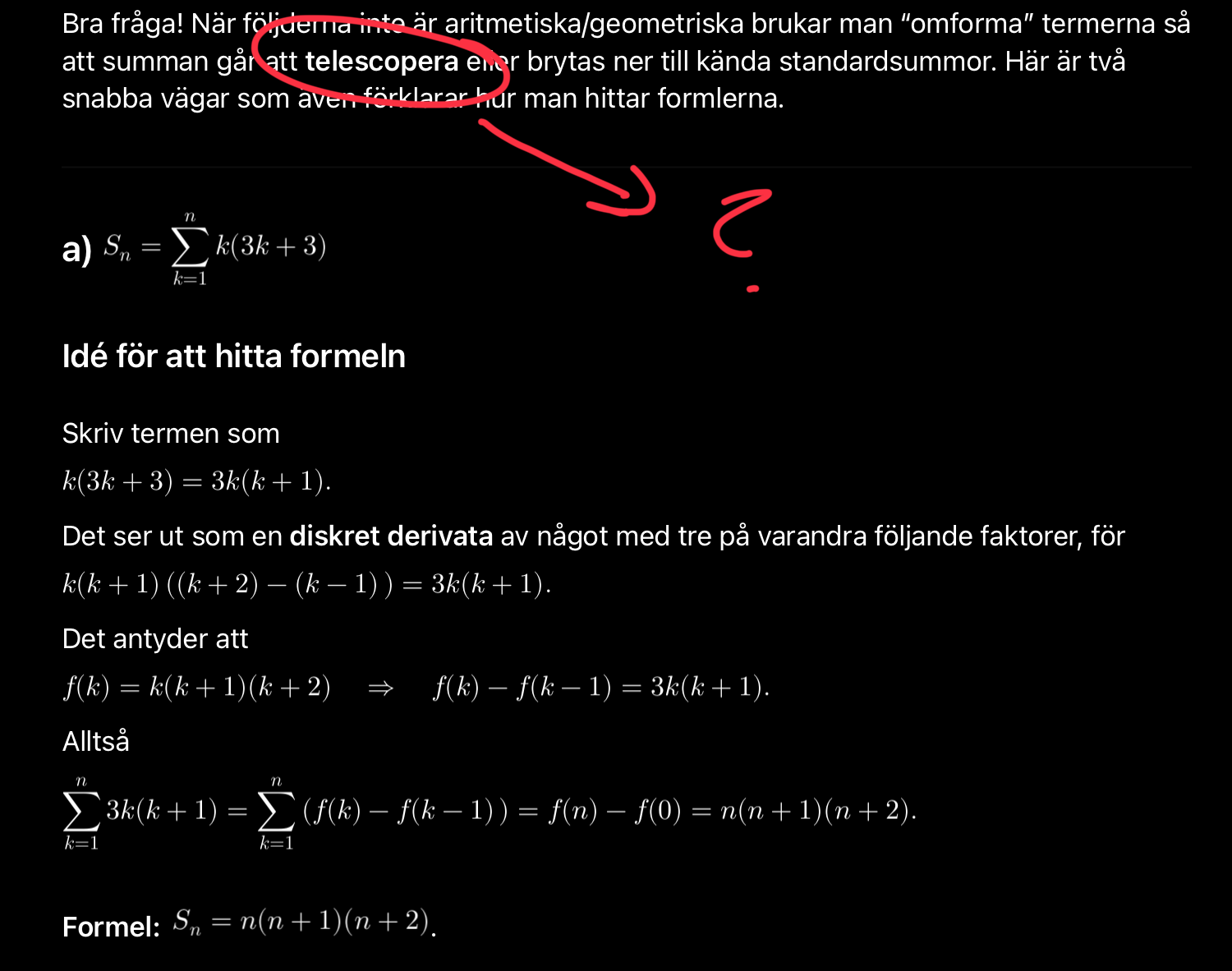Telescopering är inget som ingår i Ma5 kursen, och inget som vi ska kunna enligt läraren. Finns det andra sätt att tänka? Vad innebär telescopering?

Teleskoperande summor är summor där termer i mitten tar ut varandra. Ett exempel är summan

$\displaystyle \sum_{k=1}^{n}\left(\frac{1}{k}-\frac{1}{k+1}\right)=\frac{1}{1}{\color{red}-\frac{1}{2}+\frac{1}{2}}{\color{blue}-\frac{1}{3}+\frac{1}{3}}+...+\frac{1}{n}-\frac{1}{n+1}=1-\frac{1}{n+1}$

Att hitta slutna former är inte särskilt lätt. Det sättet jag tycker är trevligast för dessa typer är inte heller en del av ma5. Det rimligaste tycker jag är detta:

Notera att varje term i summan har formen $k(3k+3) = 3(k^2 + k)$, därmed kommer
$\displaystyle s_n = \sum_{k=1}^n k\left(3k+3\right) = 3\sum_{k=1}^n k^2 + 3\sum_{k=1}^n k$
Den senare summan är ju aritmetisk med värdet $n(n+1)/2$. Då behöver vi bara få reda på vad 
$\sum_{k=1}^n k^2$ är.

Med tanke på att summan av de första $n$ heltalen har värdet $n(n+1)/2$, vilket är ett andragradspolynom i $n$, kan det vara rimligt att gissa att summan av kvadraterna kanske blir ett tredjegradspolynom i $n$. Därmed kan vi ansätta

$\displaystyle \sum_{k=1}^n k^2 = an^3 + bn^2 + cn + d$

Sedan kan vi beräkna summan för några värden på $n$ och lösa ut $a,b,c,d$. Detta kommer ge värdet på summan, men jag vet inte hur rimligt det är att komma på denna gissning. 

Anonym_15 skrev:

Enligt ChatGPT:

Telescopering är inget som ingår i Ma5 kursen, och inget som vi ska kunna enligt läraren. Finns det andra sätt att tänka? Vad innebär telescopering?

Detta brukar ges som metod men det finns säkert flera andra, kanske bättre

Har faktiskt inte sett detta tidigare. Mycket snyggt sätt att lösa fram summorna! Min spontana tanke för att härleda dessa summor var att derivera

$\displaystyle f\left(x\right) = \sum_{k=0}^n x^k$ och ta gränsvärdet då $x\to 1$. 

Det blir nog ganska jobbigt för höga exponenter, men det är inte särskilt svårt för små. 

AlexMu skrev:

Har faktiskt inte sett detta tidigare. Mycket snyggt sätt att lösa fram summorna! Min spontana tanke för att härleda dessa summor var att derivera

$\displaystyle f\left(x\right) = \sum_{k=0}^n x^k$ och ta gränsvärdet då $x\to 1$. 

Det blir nog ganska jobbigt för höga exponenter, men det är inte särskilt svårt för små. 

Det är en listig metod, även om högre gradtal blir lite "grisiga" räkningar.

Kanske det är en sådan rekursion som Mathematica (m.fl.) använder.

Det blir inte roligt...

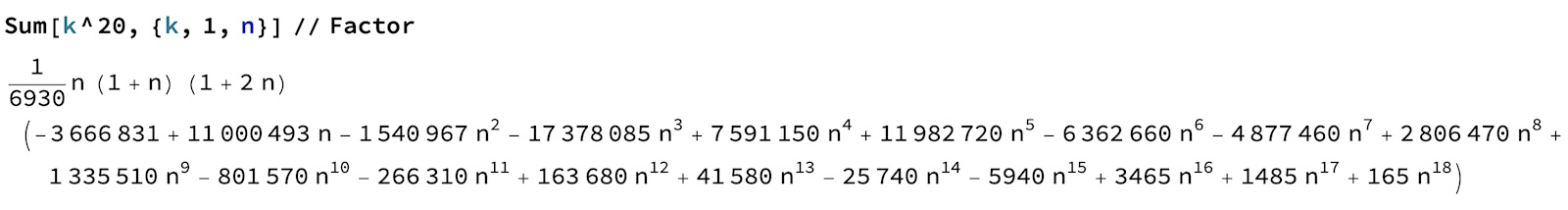
men det är intressant att både S1 och S2 (som är en form av S1) är representerade här (dock ej samtidigt). Kanske det är lätt att visa att S2 (och därmed S1) alltid är en faktor. Har ej provat.

Hmm. Det verkar som att $(1+2n)$, vilket är en del av $S_2$ inte är med om exponenten är udda 

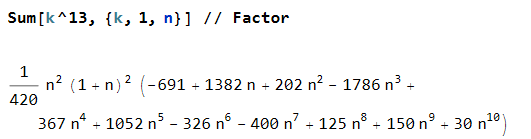
Men för jämna verkar det vara så. Kanske udda termer har $S_1$ och jämna $S_2$ (som i sin tur då har $S_1$?)

Ett annat sätt jag tänkte på för att komma fram till summorna är att utnyttja följande identitet:

Låt $a_0 = 0$. Då gäller det att

$\displaystyle \sum_{k=1}^{n}a_{k}x^{k}=\frac{1}{1-x}\sum_{k=1}^{n}\left(a_{k}-a_{k-1}\right)x^{k}-\frac{a_{n}x^{n+1}}{1-x}$

Om $a_k = k^p$ för något heltal $p$ kommer ju uttrycket

$a_k - a_{k-1} = k^p - (k-1)^p = (k^{p-1} + k^{p-2}(k-1) + \dots + (k-1)^{p-1})$, vilket är en, jobbig, kombination av alla tidigare summor, där kan det också bli någon rekursion som inte innehåller derivering. Det är förmodligen svårare än ta sig igenom derivata-iden dock.

Tillägg: 11 okt 2025 16:48

Men det bör stämma att $S_1$ alltid är en faktor. Det finns säkert ett bra sätt att visa detta, men om man går lite hårt och bara drar in den generella formeln för dessa summor: 

$\displaystyle \sum_{k=1}^n k^p = \frac{1}{p+1}\sum_{m=0}^p \left(-1\right)^m\binom{p+1}{m} B_m n^{p+1-m}$

där $B_m$ är bernoullitalen. Det enda vi behöver visa är att $n=0$ och $n=-1$ är en rot till polynomet i HL. Att $n=0$ är en rot är ganska uppenbart då vi kan faktorisera ut ett $n$. För $n=-1$ måste man visa att 

$\displaystyle \sum_{m=0}^p \binom{p+1}{m}B_m = 0$ för varje $p\geq 1$.

Jag minns att jag snubblade på denna identitet någon gång förra året. Svårighetsgraden att visa detta beror nog på hur man definierar bernoullitalen från början. Från definitionen att bernoullitalen uppfyller 

$\displaystyle \frac{x}{e^x-1} = \sum_{k=0}^\infty \frac{B_k}{k!}x^k$

kan man visa en rekursionsformeln

$\displaystyle \frac{B_0}{n! 0!} + \frac{B_1}{1! (n-1)!} + \dots + \frac{B_{n-1}}{(n-1)! 1!} = 0$ om $n>1$

vilket är ekvivalent med identiteten ovan. 

Tillägg: 13 okt 2025 15:57

Och den där rekursionsformeln följer om man multiplicerar båda led i definitionen för bernoullitalen med $e^x-1$, i VL med uttrycket och i HL med dess serie. Då ser man att koefficienterna blir själva uttrycket i rekursionsformeln. Då alla $x^n$-termer ska ha koefficient 0 förutom de första två följer identiteten. 

AlexMu: Intressant!

Jag kanske inte förstår problemet men ingen har bett om en sluten formel. ChatGPT ger en formel (som man själv "lätt" (=matte5) kommer fram till).

Jo, det står "försök sedan finna en formel för s_n".

Om man följer tipset och räknar ut s₁ till s₅ så kan man se mönstret, tycker jag. Det kan hjälpa att veta att formeln för en summa av polynomtermer är en grad större än termerna, alltså grad tre här. s_n visar sig vara väldigt nära kubiska tal.

Tack för alla lösningar! Finner det fortfarande väldigt svårt men försöker successivt förstå. Kommer nog ta lite tid:)