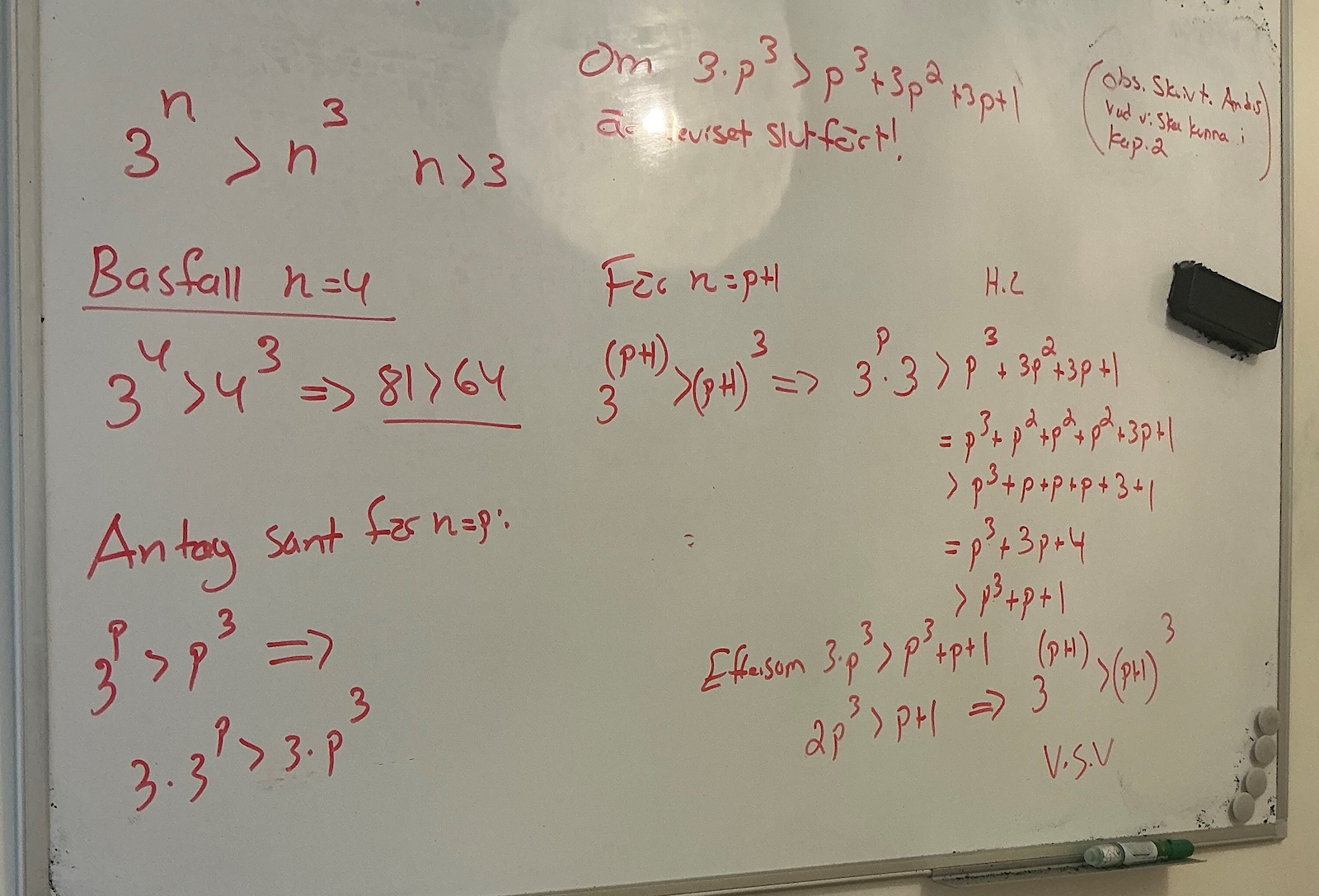Matematisk induktion, olikhet.
Hej, har jobbat ganska länge med en olikhet och undrar två saker:
1. Fungerar min metod? Skulle jag få godkänt om jag använde denna under ett prov?
2. Trots att min metod fungerar, gör jag den överkomplicerad? Kan man förenkla V.L. på ett enklare sätt?
Nedan följer både fråga och mitt svar (skriv gärna om det inte är tydligt någonstans):
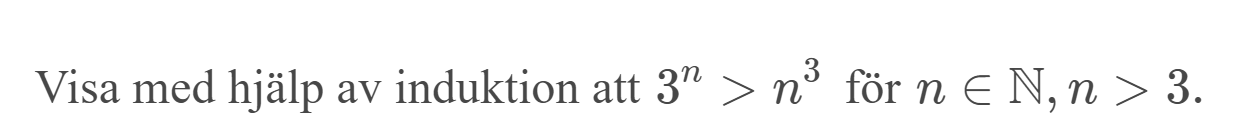
Ser bra ut. Deriveringsmetoden är ev. enklare. Svårt att veta vad de menar med "induktion" och föredragen metod.
Tack! Vilken är deriveringsmetoden?
Anonym_15 skrev:Tack! Vilken är deriveringsmetoden?
Inte så mkt med induktion nedan, men ett alternativ

Tack!
Man hajar till lite när man ser en derivering av en diskret fkn. Den har ingen derivata eftersom den inte är definierad för värden godtyckligt nära heltalet. Det man deriverar är fknen f(x)=x•ln3-3•ln x där x>0 och tillhör R. Man finner den växande för alla x>=4 och därigenom för alla heltalsvörden >=4.
Trinity2 skrev:Anonym_15 skrev:Tack! Vilken är deriveringsmetoden?
Inte så mkt med induktion nedan, men ett alternativ
Har en fråga angående din lösning. Måste man logaritmera? Går det att skapa funktionen, utan att logaritmera, och sedan bevisa att derivatan är positiva för alla n större än 3?
Anonym_15 skrev:Trinity2 skrev:Anonym_15 skrev:Tack! Vilken är deriveringsmetoden?
Inte så mkt med induktion nedan, men ett alternativ
Har en fråga angående din lösning. Måste man logaritmera? Går det att skapa funktionen, utan att logaritmera, och sedan bevisa att derivatan är positiva för alla n större än 3?
Går bra

Hej, är tillbaka igen. Vill fråga om denna metod (där ett led reduceras för att likna ett annat) innebär att man får hålla på att reducera hur som helst så länge olikheten fortfarande gäller? Eller inte?
Detta är ju ett annat exempel på samma uppgift, bara att ledet nu är reducerat på annat sätt: