Matrismultiplikation med invers

Hej! har en fundering. I frågan Lös ekvationen $A X = X + A B$

Gjorde jag för ett tag sedan lösningen: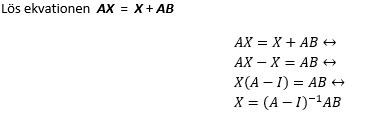

Men nu när jag ser i efterhand undrade jag om det verkligen är rätt?

Med tanke på att ${(A - I)}^{- 1}$ är en högerinvers borde väl ekvationen istället få lösningen

$A X = X + A B \Leftrightarrow A X - X = A B \Leftrightarrow X (A - I) {(A - I)}^{- 1} = A B {(A - I)}^{- 1}$

Eller är det bara jag som blir förvirrad och gör det svårare än det behöver vara?

Tacksam för hjälp!

Det är en vänsterinvers: $AX - X = AB \Leftrightarrow AX - IX = AB \Leftrightarrow (A-I)X = AB \Leftrightarrow X = (A-I)^{-1}AB$ (om inverterbar)

Inabsurdum skrev:
Det är en vänsterinvers: $AX - X = AB \Leftrightarrow AX - IX = AB \Leftrightarrow (A-I)X = AB \Leftrightarrow X = (A-I)^{-1}AB$ (om inverterbar)

Det förklarar varför jag fick rätt på uppgiften när den rättades alltså. Men hur kan jag veta att jag ska skriva om $A X - X \Leftrightarrow (A - I) X$ och inte $A X - X = X (A - I)$

Är det allmänt vedertaget enligt någon regel?

Det bygger på att matrismultiplikation inte är kommutativ.

Svara

Visa senaste svar