Matte uppgift från tävling för åk 9
Hej, jag har försökt att lösa denna uppgift men jag kommer ingen vart. Vet inte ens hur jag ska börja efter jag ritat upp figuren. Det skall ej krävas mer kunskap än det man lär sig i åk 9.
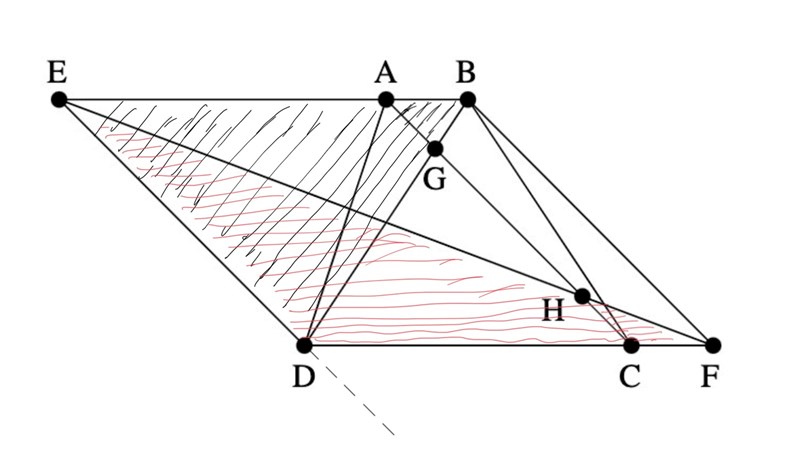
5. I parallelltrapetset ABCD är AB och CD parallella. Förläng BA till E så att |AE| =
|CD| och A ligger mellan B och E. Förläng på samma sätt DC till F så att |CF| = |AB|
och C ligger mellan D och F. Låt G vara skärningspunkten för diagonalerna AC och BD,
och låt H vara skärningspunkten för AC och EF. Visa att |AG| = |CH|.
(Beteckningen |AB| betyder längden från A till B.)
ladda upp din figur
Edit: Så här tolkar jag uppgiften: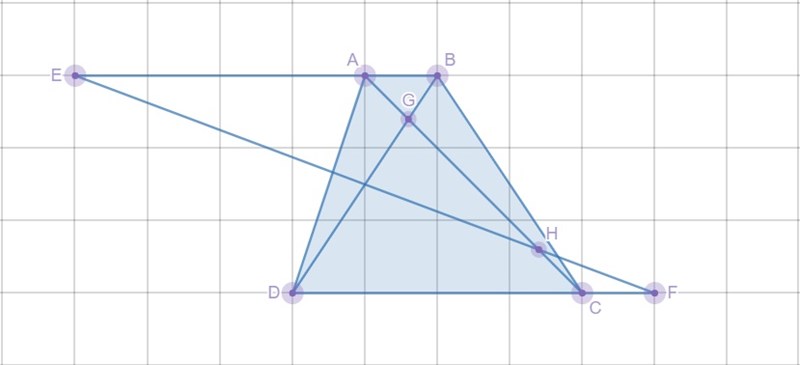 Är det så du tolkar den?
Är det så du tolkar den?
Ja!
Vänta lite så länge jag kan få reda på att triangel ABG och CHF är likbenta så är de klatt.
:)
Vinkeln AHE är lika med CHF, och AEH är lika med CFH.
Tillägg: 2 nov 2021 14:43
Jag kan fortfarande ej lösa uppgiften :/
Jag tror att hjälplinjer som visar att det alltid blir ett parallellogram kan hjälpa:
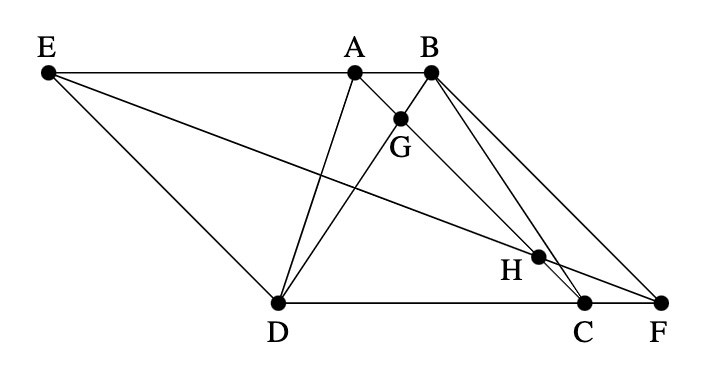
Samma figur lite städad:
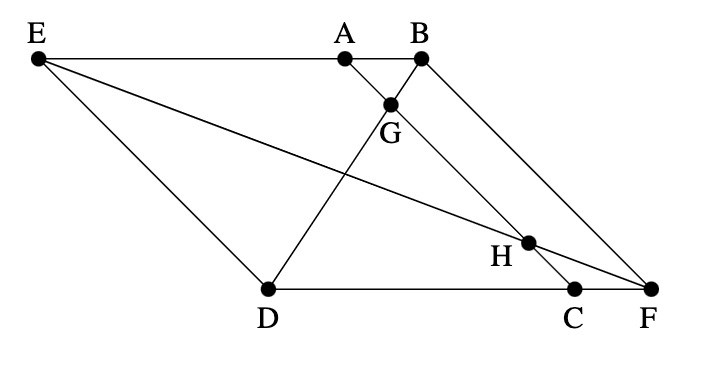
När det är en rektangel är beviset uppenbart (symmetri):
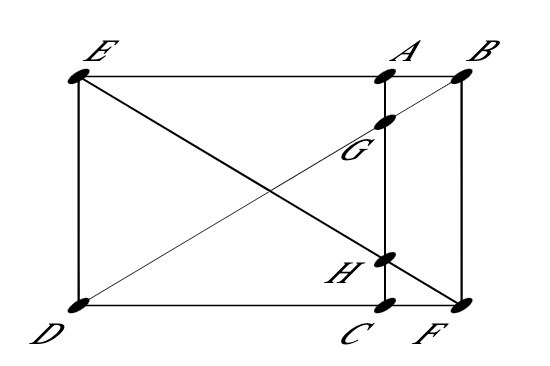
Men i ett parallellogram har sidorna alltid samma längd oavsett lutning. AG och CH måste således ha samma längd oavsett lutningen, dvs oavsett hur den ursprungliga parallelltrapetsen såg ut.
Känner mig dock inte helt nöjd, går säkert att visa det mycket snyggare.
Jag gillar Programmerarens visuella bevis. Väldigt tydligt.
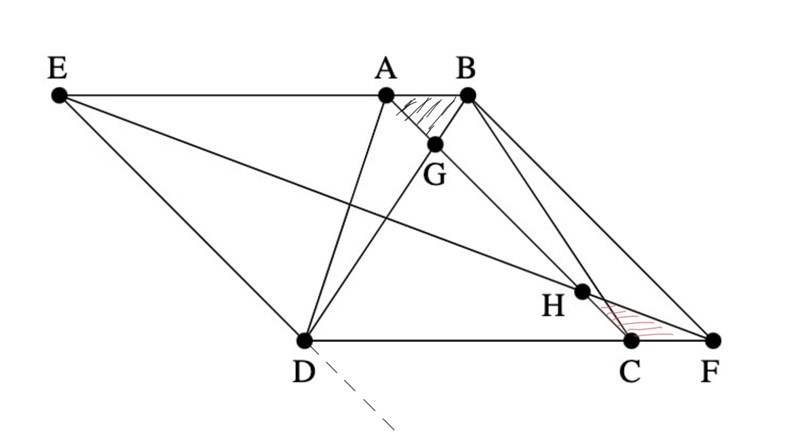
Jag tänkte mer på likformigheten med "Vinkeln AHE är lika med CHF, och AEH är lika med CFH." Det ger att EAH=HCF
Det ger 2 trianglar som har alla vinklar lika. Och eftersom |CF| återfinns i båda trianglarna kommer alla sidor vara lika, även |AG|=|CH|
Här har jag tagit trinageln CFH och roterat och transporterat den för att visa tydligare:
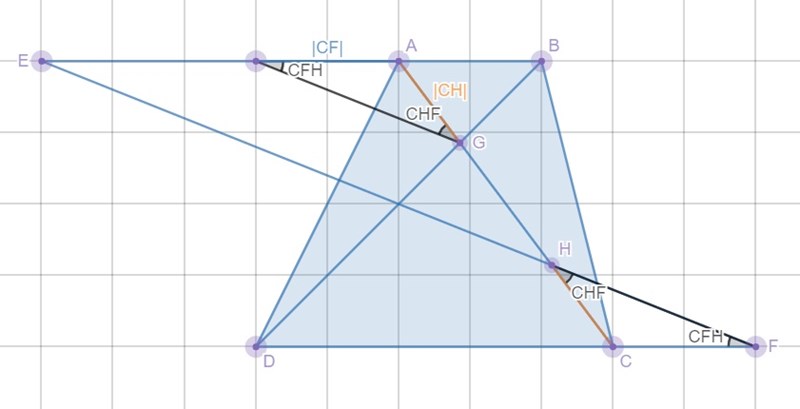
De båda stora streckade trianglarna är lika stora, eftersom de har gemensam bas och samma höjd sett från ED. De små streckade trianglarna är likformiga med de större, deras baser är parallella med ED och har då samma ytor. Då är också AG = HC.