Maximala arean - matte 3c

Jag har fastnat en stund på denna uppgift:

En lantbrukare har för avsikt att bygga en rektangulär delad hage, där varje liten hage
har samma storlek, enligt figurens utseende. Han har 800 m staket till sitt förfogande.

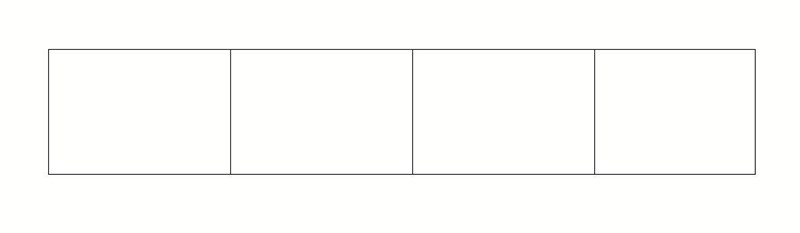
Vilka mått ska han använda för att få maximal area på hagarna?

Det jag kommit fram till är att:

Staketets längd: y a.e.

Staketets bred: x a.e.

Arean (staket) : x * y a.e.

Fyra lika stora hagar: A= 3xy

Staketets omkrets: 8x + 5y = 800 m

y= 160x - 1,6x

A(x) = xy = 160x - 1,6x^2

Välkommen till Pluggakuten! Det är en mycket bra början! Det enda jag är fundersam över är varför fyra lika stora hagar har arean 3xy. Borde inte den totala arean vara 4xy? Då blir din formel $A(x)=4(160x-1,6x^2)$ . För att hitta maximum, vad händer om du deriverar funktionen? :)

Oj, det hade jag inte tänkt på, om jag nu gjorde så fick jag att:

$A (x) = 4 (160 x - 1, 6 x^{2}) = 640 x - 6, 4 x^{2} o c h o m m a n d e r i v e r a r d e t f å r m a n A' (x) = 640 - 12, 8 x f ö r a t t s e d a n h i t t a m a x i m i p u n k t e n 640 - 12, 8 x = 0 s o m g e r a t t x = 50 o c h d å s ä t t e r m a n i n d e t i u t t r y c k e t f ö r o m k r e t s e n 8 \times 50 + 5 y = 800 v i l k e t g e r a t t y = 80 S v a r : k o r t s i d a n y = 80 m o c h l å n g s i d a n x = 50 \times 4 = 200 m$

Det låter vettigt. Vad blir då den maximala arean? :)

Maximala area: 80x200= 16 000m2

Bra! :)

Svara

Visa senaste svar