maximala arean på en rektangel i ett koordinatsystem? (Matematik/Matte 3/Algebraiska uttryck)

Det borde stå att det där motsatta hörnet ska ha positivt y, eller något likvärdigt, som att en sida ska ligga på positiva y-axeln. Annars kan jag göra en mycket stor rektangel.

Om du får ut maximala arean grafiskt utan problem är jag orolig för att något är fel. Kan du visa din bild?

Laguna skrev:
Det borde stå att det där motsatta hörnet ska ha positivt y, eller något likvärdigt, som att en sida ska ligga på positiva y-axeln. Annars kan jag göra en mycket stor rektangel.

Hur gör du då? Kan du lägga in en bild?

Smaragdalena skrev:
Laguna skrev:
Det borde stå att det där motsatta hörnet ska ha positivt y, eller något likvärdigt, som att en sida ska ligga på positiva y-axeln. Annars kan jag göra en mycket stor rektangel.
Hur gör du då? Kan du lägga in en bild?

Jag ska, men jag väntar på att frågeställaren säger något mer. T.ex. en bild eller hur stor arean blev.

Om ett hörn på rektangeln skall vara i origo, och en sida skall vara längs positiva x-axeln, så skulle rektangeln kunna gå uppåt, och då kan det motsatta hörnet ligga på den räta linjen, eller också kan rektangeln gå neråt, och i så fall träffar man aldrig på den räta linjen. Uppgiften är tydlig.

EDIT: Laguna har rätt, jag hade fel. Uppgiften är tvetydig. Antingen finns det en rektangel i den första kvadranten som man kan beräkna maximal area för, eller så finns det en rektangel i fjärde kvadranten som kan bli hur stor som helst.

Smaragdalena skrev:
Om ett hörn på rektangeln skall vara i origo, och en sida skall vara längs positiva x-axeln, så skulle rektangeln kunna gå uppåt, och då kan det motsatta hörnet ligga på den räta linjen, eller också kan rektangeln gå neråt, och i så fall träffar man aldrig på den räta linjen. Uppgiften är tydlig.

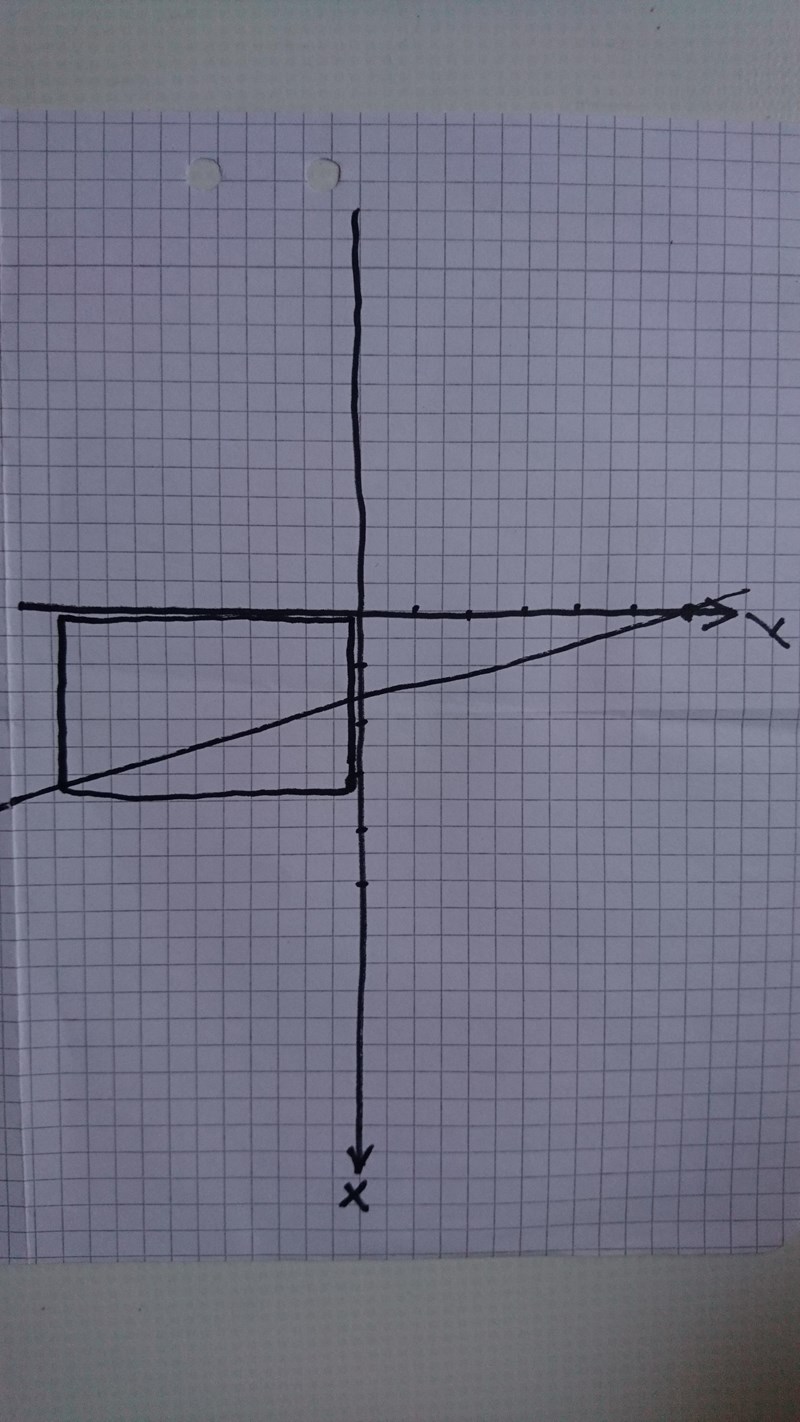
Bilden stämmer inte heller då linjen inte är den som anges i uppgiften. Den har en negativ lutning. Därmed kan man rita en rektangel i fjärde kvadranten som uppfyller alla vilkor. Dock skulle jag anta att rektangeln skall ligga i första kvadranten.

AndersW skrev:
Bilden stämmer inte heller då linjen inte är den som anges i uppgiften. Den har en negativ lutning. Därmed kan man rita en rektangel i fjärde kvadranten som uppfyller alla vilkor. Dock skulle jag anta att rektangeln skall ligga i första kvadranten.

Bilden är vriden, och det är mitt fel, men du ser ju var x och y är. "Anta" ska du inte göra.

Smaragdalena skrev:
Om ett hörn på rektangeln skall vara i origo, och en sida skall vara längs positiva x-axeln, så skulle rektangeln kunna gå uppåt, och då kan det motsatta hörnet ligga på den räta linjen, eller också kan rektangeln gå neråt, och i så fall träffar man aldrig på den räta linjen. Uppgiften är tydlig.

jag sitter med den här uppgiften också men jag sitter fast någonstans. Jag har ritat ut linjen men huruvida vart rektangeln ska ritas är för mig oklart.. Linjen skär y-axeln i 6 och har negativ riktningskofficient på 4. Och så har vi rektangeln som ligger med ett hörn i origo, vilket hörn i koordinatsystemet har jag inte kunnat listat ut.

Om det inte står i uppgiften att "det motsatta hörnet" skall ligga i första kvadranten, så har Laguna rätt i att rektangeln kan bli så stor man vill. Kan du lägga in en bild av uppgiften?

Smaragdalena skrev:
Om det inte står i uppgiften att "det motsatta hörnet" skall ligga i första kvadranten, så har Laguna rätt i att rektangeln kan bli så stor man vill. Kan du lägga in en bild av uppgiften?

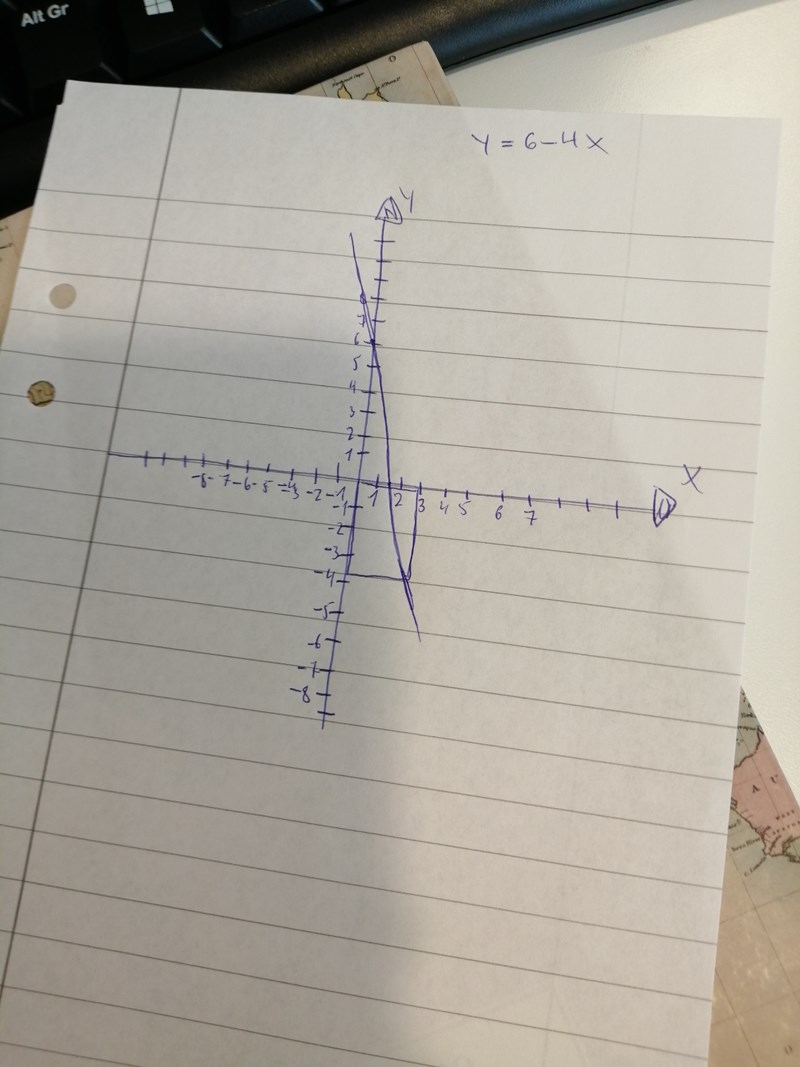hej

stämmer detta?

(har tyvärr för tillfället ej tillgång till rutat papper).

Alltid tacksam för all hjälp.

/Nina

Hur är uppgiften formulerad (exakt)? Lägg gärna in en bild.

Smaragdalena skrev:
Hur är uppgiften formulerad (exakt)? Lägg gärna in en bild.

En rektangel ligger med ett hörn i origo, det motsatta hörnet på linjen y=6-4x och en sida på positiva x-axeln. Bestäm den maximala arean på rektangeln under dessa förutsättningar.

Jag har ritat upp linjen, rektangeln där jag tror att den ska vara på koordinatsystemet. Men hur bestämmer jag den maximala arean? Vi vet ju varken rektangelns höjd eller bredd.

anonymousnina skrev:
Smaragdalena skrev:
Hur är uppgiften formulerad (exakt)? Lägg gärna in en bild.
En rektangel ligger med ett hörn i origo, det motsatta hörnet på linjen y=6-4x och en sida på positiva x-axeln. Bestäm den maximala arean på rektangeln under dessa förutsättningar.

Jag har ritat upp linjen, rektangeln där jag tror att den ska vara på koordinatsystemet. Men hur bestämmer jag den maximala arean? Vi vet ju varken rektangelns höjd eller bredd.

Uppgiften är olyckligt formulerad.

Det finns nämligen två möjliga rektanglar som uppfyller villkoren.

Den ena har du ritat och lagt in en bild av lite tidigare i denna tråd. Den rektangeln har ingen övre areabegränsning eftersom det nedre högra hörnets x-koordinat kan vara hur stor som helst.

Kan du hitta den andra rektangeln som uppfyller villkoren? Den har en övre gräns för sin area.

Yngve skrev:
anonymousnina skrev:
Smaragdalena skrev:
Hur är uppgiften formulerad (exakt)? Lägg gärna in en bild.
En rektangel ligger med ett hörn i origo, det motsatta hörnet på linjen y=6-4x och en sida på positiva x-axeln. Bestäm den maximala arean på rektangeln under dessa förutsättningar.

Jag har ritat upp linjen, rektangeln där jag tror att den ska vara på koordinatsystemet. Men hur bestämmer jag den maximala arean? Vi vet ju varken rektangelns höjd eller bredd.
Uppgiften är olyckligt formulerad.
Det finns nämligen två möjliga rektanglar som uppfyller villkoren.
Den ena har du ritat och lagt in en bild av lite tidigare i denna tråd. Den rektangeln har ingen övre areabegränsning eftersom det nedre högra hörnets x-koordinat kan vara hur stor som helst.
Kan du hitta den andra rektangeln som uppfyller villkoren? Den har en övre gräns för sin area.

Ok det betyder alltså att man inte kan beräkna arean för den rektangeln? Om jag nu redovisar som på bilden när jag lämnar in detta, blir det felaktigt då? De villkoren som finns är ju att det ligger som ett hörn i origo. Det står på den positiva y-sidan i uppgiften. Så då kan jag bara rita upp den på positiva y-sidan och genom att jag vet hur linjen går kan jag beräkna maximala arean. Antar att det bara är höjden gånger bredden?

anonymousnina skrev:

...
Det står på den positiva y-sidan i uppgiften.
...

Det skrev du inte tidigare. Vad är det som gäller egentligen?

Kan du för säkerhets skull ladda upp en bild av själva uppgiftslydelsen?

Yngve skrev:
anonymousnina skrev:
...
Det står på den positiva y-sidan i uppgiften.
...
Det skrev du inte tidigare. Vad är det som gäller egentligen?
Kan du för säkerhets skull ladda upp en bild av själva uppgiftslydelsen?

Ursäkta jag läste fel o därav skrev fel, det skulle stå *och en sida på positiva x-axeln. Uppgiften jag har är precis den som i inlägget.

anonymousnina skrev:

Ursäkta jag läste fel o därav skrev fel, det skulle stå *och en sida på positiva x-axeln. Uppgiften jag har är precis den som i inlägget.

OK bra. Då gäller det jag skrev tidigare, att det finns två fall.

Det ena har du hittat. Hittar du det andra, det där rektangeln har en övre gräns för sin area?

Yngve skrev:
anonymousnina skrev:
Ursäkta jag läste fel o därav skrev fel, det skulle stå *och en sida på positiva x-axeln. Uppgiften jag har är precis den som i inlägget.
OK bra. Då gäller det jag skrev tidigare, att det finns två fall.
Det ena har du hittat. Hittar du det andra, det där rektangeln har en övre gräns för sin area?

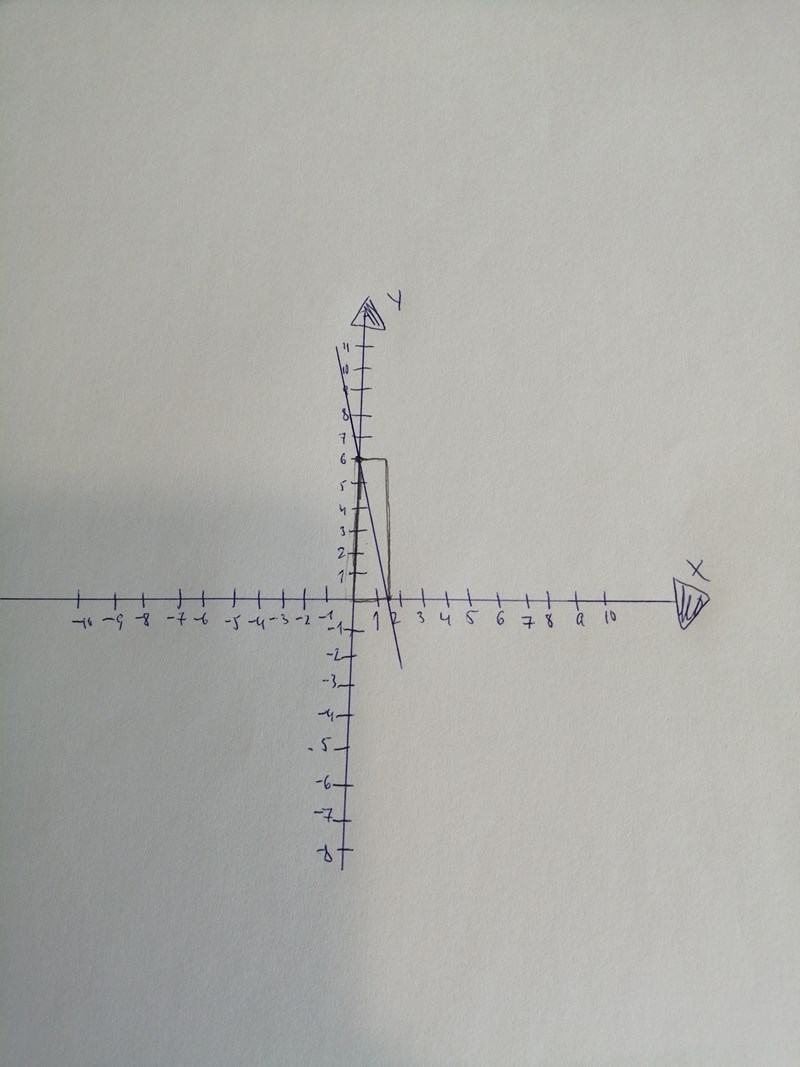
anonymousnina skrev:
Yngve skrev:
anonymousnina skrev:
Ursäkta jag läste fel o därav skrev fel, det skulle stå *och en sida på positiva x-axeln. Uppgiften jag har är precis den som i inlägget.
OK bra. Då gäller det jag skrev tidigare, att det finns två fall.
Det ena har du hittat. Hittar du det andra, det där rektangeln har en övre gräns för sin area?

"En rektangel ligger med ett hörn i origo, det motsatta hörnet på linjen".

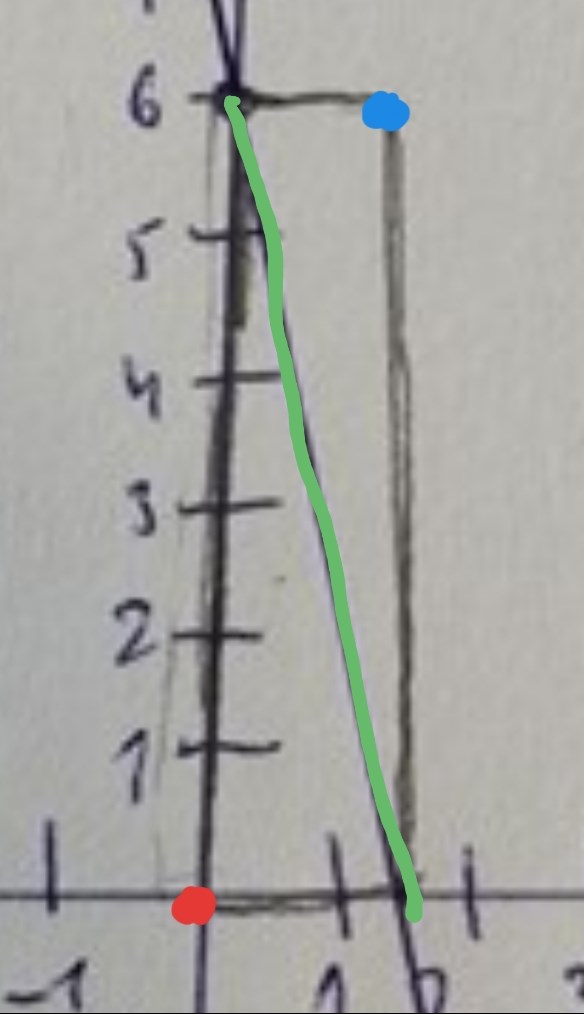
Förklaring: Det (till hörnet i origo) motsatta hörnet är det hörn som ligger längst från origo, dvs det hörn som ligger på diagonalen, se figur.

Rött = hörnet i origo
Blått = motsatt hörn

Om du minskar bredden och höjden på rektangeln så kommer det blåa hörnet att hamna på linjen som det ska.

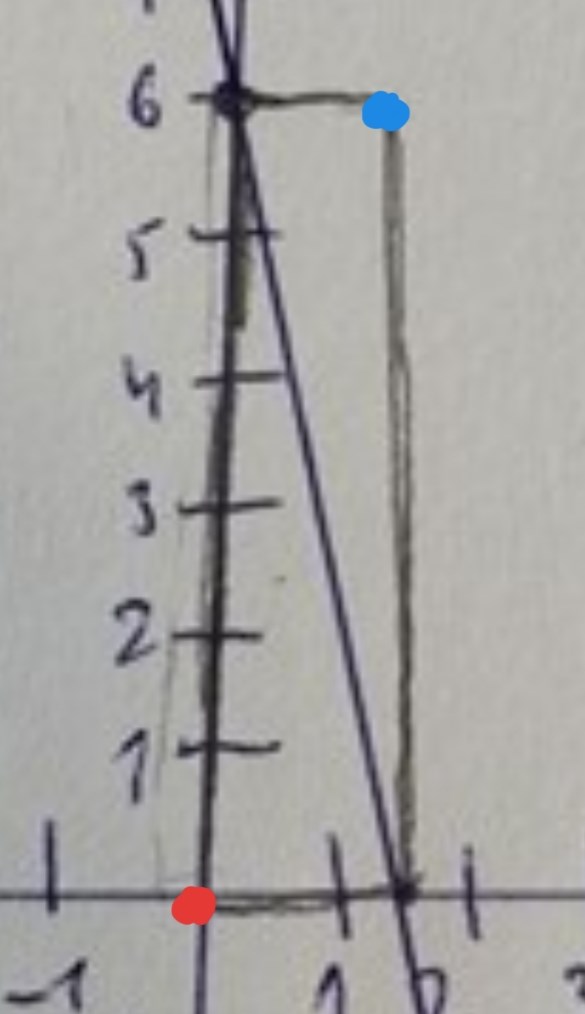
Yngve skrev:
Förklaring: Det (till hörnet i origo) motsatta hörnet är det hörn som ligger längst från origo, dvs det hörn som ligger på diagonalen, se figur.
Rött = hörnet i origo
Blått = motsatt hörn
Om du minskar bredden och höjden på rektangeln så kommer det blåa hörnet att hamna på linjen som det ska.

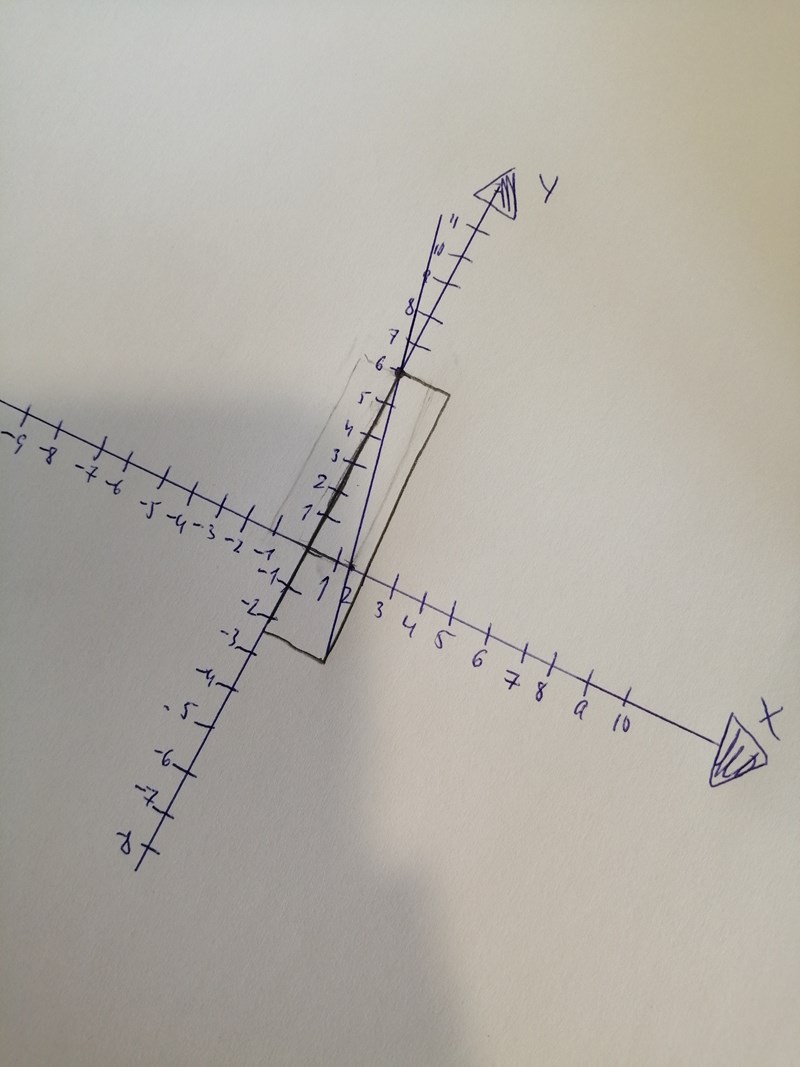
Så här? Får jag fråga hur du kunde läsa av från uppgiften att det rör sig om två rektanglar? Varav en ej fyller villkoren. Jag ska redovisa det här muntligt så behöver verkligen förstå allt.

Tack på förhand

/Nina

Kan du peka ut det motsatta hörnet som vi talar om? Ser du att det inte ligger på linjen i din bild?

Laguna skrev:
Kan du peka ut det motsatta hörnet som vi talar om? Ser du att det inte ligger på linjen i din bild?

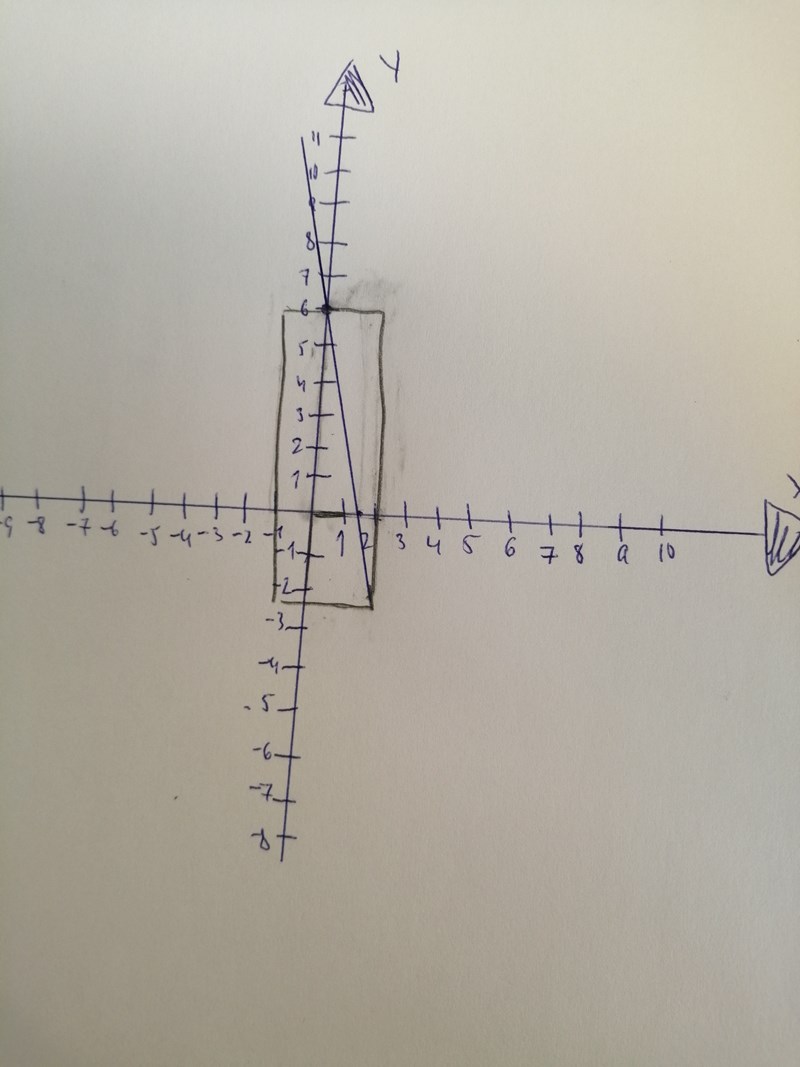
anonymousnina skrev:
Laguna skrev:
Kan du peka ut det motsatta hörnet som vi talar om? Ser du att det inte ligger på linjen i din bild?

Nej nu har du dels flyttat det röda hörnet så att det inte längre ligger i origo, dels flyttat det blåa hörnet åt fel håll (åt höger).

Du skulle istället flytta det blåa hörnet så att det ligger på den gröna linjen.

Gör så här: Låt det röda hörnet vara kvar i origo och minska rektangelns storlek så pass mycket att det blåa hörnet hamnar på den gröna linjen.

Yngve skrev:
anonymousnina skrev:
Laguna skrev:
Kan du peka ut det motsatta hörnet som vi talar om? Ser du att det inte ligger på linjen i din bild?
Nej nu har du flyttat det röda hörnet så att det inte längre ligger i origo.
Du skulle istället flytta det blåa hörnet så att det ligger på den gröna linjen. Det röda hörnet ska vara kvar i origo.

anonymousnina skrev:
Yngve skrev:
anonymousnina skrev:
Laguna skrev:
Kan du peka ut det motsatta hörnet som vi talar om? Ser du att det inte ligger på linjen i din bild?
Nej nu har du flyttat det röda hörnet så att det inte längre ligger i origo.
Du skulle istället flytta det blåa hörnet så att det ligger på den gröna linjen. Det röda hörnet ska vara kvar i origo.

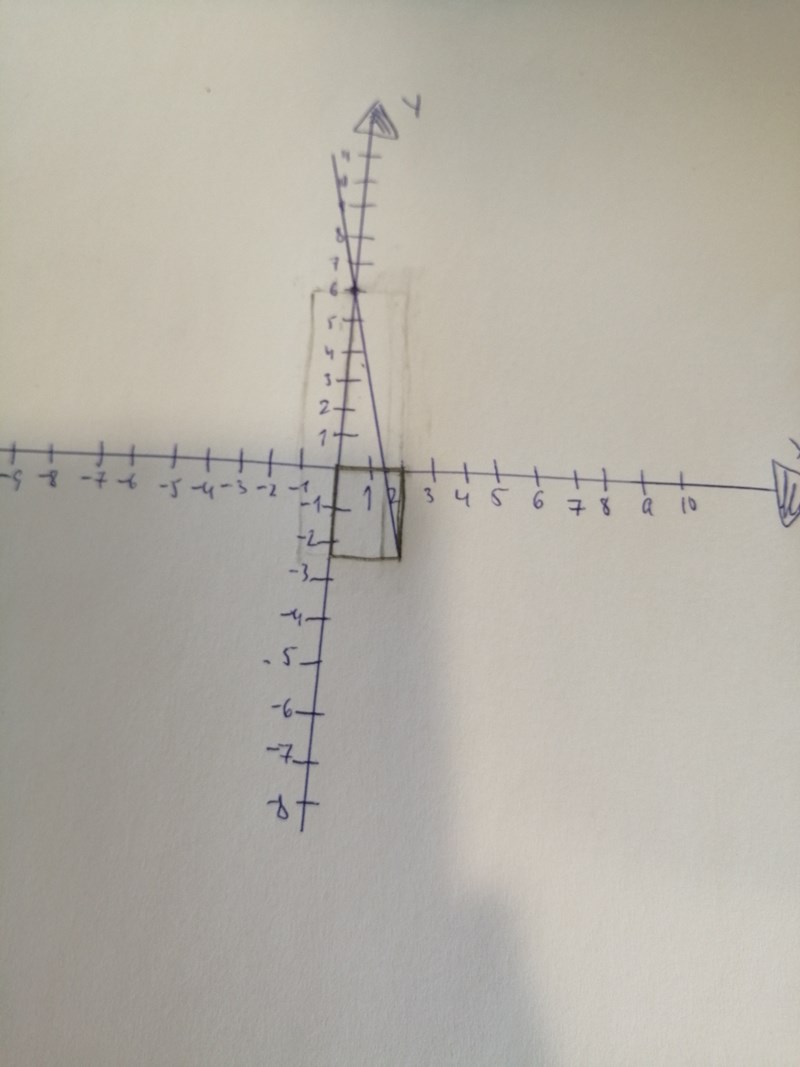
Nu ligger det inte ens ett hörn i origo. Läs igenom allt som har sagts, långsamt och noggrant.

Laguna skrev:
Nu ligger det inte ens ett hörn i origo. Läs igenom allt som har sagts, långsamt och noggrant.

Jag skulle flytta det blåa hörnet till till den gröna linjen och låta det röda hörnet vara kvar. Tyvärr hänger jag inte med här ):

anonymousnina skrev:
Laguna skrev:
Nu ligger det inte ens ett hörn i origo. Läs igenom allt som har sagts, långsamt och noggrant.
Jag skulle flytta det blåa hörnet till till den gröna linjen och låta det röda hörnet vara kvar. Tyvärr hänger jag inte med här ):

Flytta det blåa hörnet, t.ex. enligt den lila pilen. Rita den nya rektangeln. Visa den nya rektangeln för oss.

anonymousnina skrev:
Laguna skrev:
Nu ligger det inte ens ett hörn i origo. Läs igenom allt som har sagts, långsamt och noggrant.
Jag skulle flytta det blåa hörnet till till den gröna linjen och låta det röda hörnet vara kvar. Tyvärr hänger jag inte med här ):

Jag såg delvis fel, för det du hade suddat var kvar.

Jag såg också fel, jag Trodde att din nya rektangel var den här:

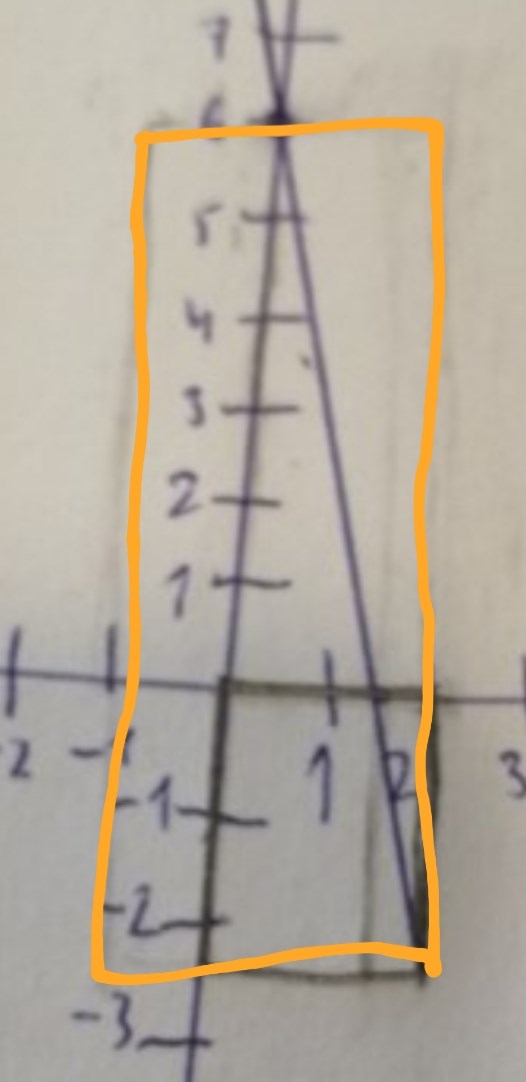
Yngve skrev:
Jag såg också fel, jag Trodde att din nya rektangel var den här:

Ok jag förstår, då stämmer alltså den rektangel på min senaste bild?

Ok jag förstår, då stämmer alltså den rektangel på min senaste bild?

Nej, inte om det skall vara den rektangel som man kan beräkna en maximal area för. Den rektangeln har ett hörn i origo, ett hörn på den blå (i din bild) linjen, en sida längs positiva x-axeln och en sida längs positiva y-axeln.

anonymousnina skrev:

Ok jag förstår, då stämmer alltså den rektangel på min senaste bild?

Nej.

Egentligen ville jag att du skulle komma på det själv, men det verkar ha gått i baklås, så jag visar här hur vi menar.

I det ena fallet ligger rektangeln under x-axeln. Denna rektangel har ingen övre begränsning av sin area, eftersom det nedre högra hörnet kan vara hur långt bort från origo som helst.

Exempel:

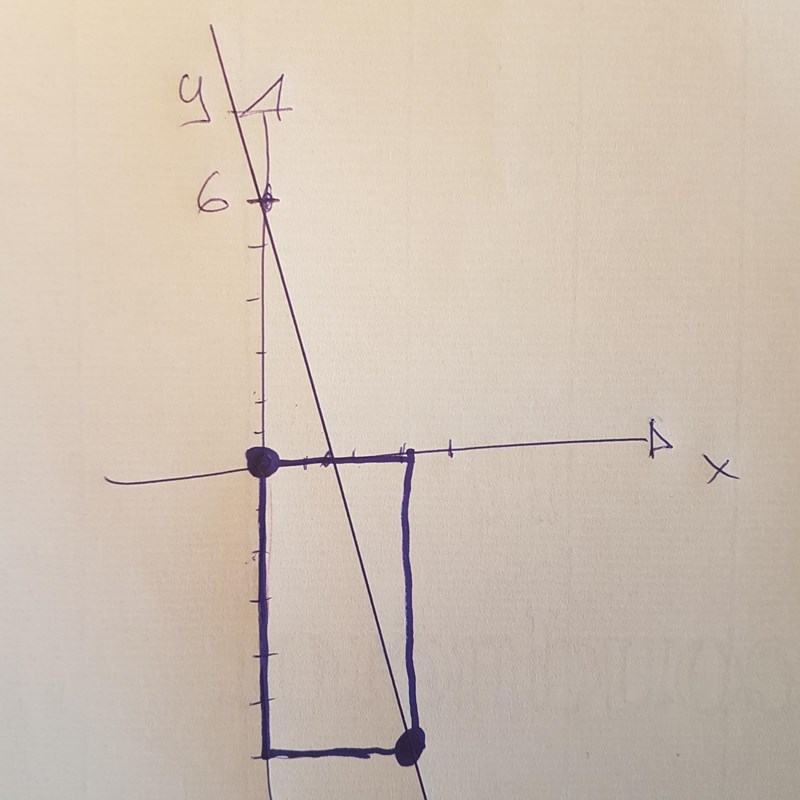
I det andra fallet ligger rektangeln över x-axeln. Denna rektangel har en övre begränsning av sin area eftersom det övre högra hörnet är "instängt" mellan positiva y-axeln och positiva x-axeln, dvs mellan punkterna (0: 6) och (1,5: 0).

Exempel:

-----------

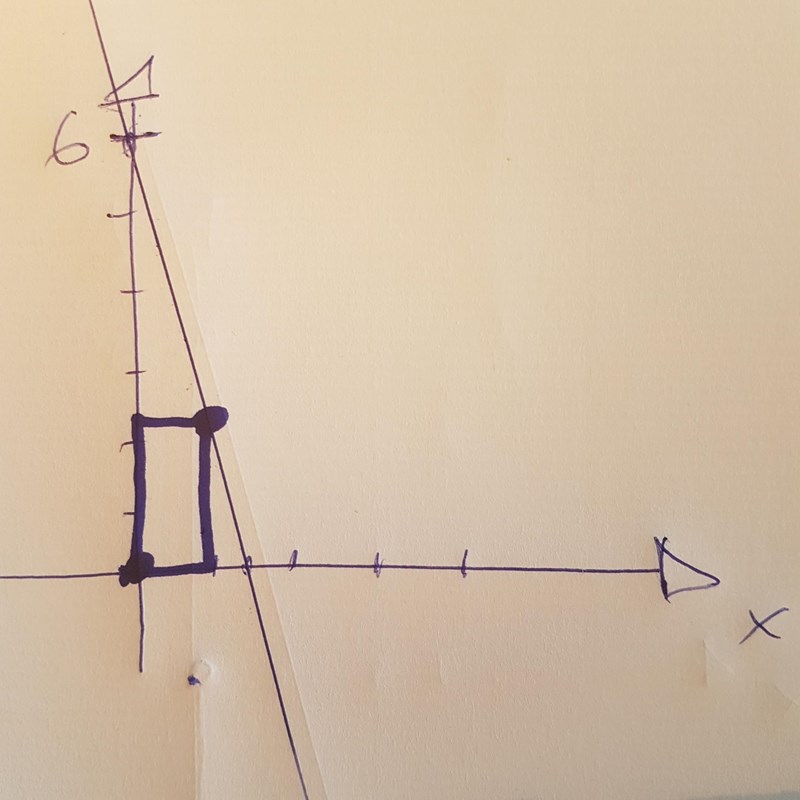
Båda dessa rektanglar uppfyller villkoren i uppgiften, vilket är orsaken till att jag skrev att uppgiften är olyckligt formulerad.

Yngve skrev:
anonymousnina skrev:
Ok jag förstår, då stämmer alltså den rektangel på min senaste bild?
Nej.
Egentligen ville jag att du skulle komma på det själv, men det verkar ha gått i baklås, så jag visar här hur vi menar.
I det ena fallet ligger rektangeln under x-axeln. Denna rektangel har ingen övre begränsning av sin area, eftersom det nedre högra hörnet kan vara hur långt bort från origo som helst.
Exempel:
I det andra fallet ligger rektangeln över x-axeln. Denna rektangel har en övre begränsning av sin area eftersom det övre högra hörnet är "instängt" mellan positiva y-axeln och positiva x-axeln, dvs mellan punkterna (0: 6) och (1,5: 0).
Exempel:
-----------
Båda dessa rektanglar uppfyller villkoren i uppgiften, vilket är orsaken till att jag skrev att uppgiften är olyckligt formulerad.

Ok tack för din förklaring. Tyvärr är inte Matte mitt starkaste ämne, och det gör ju inte saken bättre över att det är över en tråd på nätet. Hade ju varit så mycket enklare om det var på en lektion.
Hur som helst.
Då förstår jag alltså hur rektangeln uppfyller villkoren i uppgiften; och att den då är begränsad till skillnad den andra rektangeln. När jag nu ska beräkna arean:
Då blir det basen gånger höjden: i detta fall 1 (basen) gånger höjden (2) - 1 gånger 2= 2

Omkretsen blir då 1+1-2-2= 6

Men nu frågas det ju efter den maximala arean? Hur ska jag tänka då?

anonymousnina skrev:

Ok tack för din förklaring. Tyvärr är inte Matte mitt starkaste ämne, och det gör ju inte saken bättre över att det är över en tråd på nätet. Hade ju varit så mycket enklare om det var på en lektion.

Hur som helst.
Då förstår jag alltså hur rektangeln uppfyller villkoren i uppgiften; och att den då är begränsad till skillnad den andra rektangeln. När jag nu ska beräkna arean:
Då blir det basen gånger höjden: i detta fall 1 (basen) gånger höjden (2) - 1 gånger 2= 2
Omkretsen blir då 1+1-2-2= 6

Men nu frågas det ju efter den maximala arean? Hur ska jag tänka då?

Du har rätt i att rektangelns area är basen gånger höjden.

Är du med på att om övre högra hörnet har koordinaterna (x: y) så är basen x och höjden y?

Yngve skrev:
anonymousnina skrev:
Ok tack för din förklaring. Tyvärr är inte Matte mitt starkaste ämne, och det gör ju inte saken bättre över att det är över en tråd på nätet. Hade ju varit så mycket enklare om det var på en lektion.
Hur som helst.
Då förstår jag alltså hur rektangeln uppfyller villkoren i uppgiften; och att den då är begränsad till skillnad den andra rektangeln. När jag nu ska beräkna arean:
Då blir det basen gånger höjden: i detta fall 1 (basen) gånger höjden (2) - 1 gånger 2= 2
Omkretsen blir då 1+1-2-2= 6

Men nu frågas det ju efter den maximala arean? Hur ska jag tänka då?
Du har rätt i att rektangelns area är basen gånger höjden.
Är du med på att om övre högra hörnet har koordinaterna (x: y) så är basen x och höjden y?

Ja precis, Basen x är 1 och höjden y är 2.

Men hur kan jag räkna fram den maximala arean?

anonymousnina skrev:
Yngve skrev:
anonymousnina skrev:
Ok tack för din förklaring. Tyvärr är inte Matte mitt starkaste ämne, och det gör ju inte saken bättre över att det är över en tråd på nätet. Hade ju varit så mycket enklare om det var på en lektion.
Hur som helst.
Då förstår jag alltså hur rektangeln uppfyller villkoren i uppgiften; och att den då är begränsad till skillnad den andra rektangeln. När jag nu ska beräkna arean:
Då blir det basen gånger höjden: i detta fall 1 (basen) gånger höjden (2) - 1 gånger 2= 2
Omkretsen blir då 1+1-2-2= 6

Men nu frågas det ju efter den maximala arean? Hur ska jag tänka då?
Du har rätt i att rektangelns area är basen gånger höjden.
Är du med på att om övre högra hörnet har koordinaterna (x: y) så är basen x och höjden y?
Ja precis, Basen x är 1 och höjden y är 2.
Men hur kan jag räkna fram den maximala arean?

Nej, det stämmer inte. Jag tror att du skall rita en gång till och lägga in bilden här igen. Ett hörn skall ligga i origo, ett hörn skall ligga i punkten (x,0), ett hörn skall ligga i punkten (x,y) och ett hörn skall ligga i punkten (0,y) där y=6-4x d v s hörnet (x,y) skall ligga på linjen y=6-4x.

Smaragdalena skrev:
anonymousnina skrev:
Yngve skrev:
anonymousnina skrev:
Ok tack för din förklaring. Tyvärr är inte Matte mitt starkaste ämne, och det gör ju inte saken bättre över att det är över en tråd på nätet. Hade ju varit så mycket enklare om det var på en lektion.
Hur som helst.
Då förstår jag alltså hur rektangeln uppfyller villkoren i uppgiften; och att den då är begränsad till skillnad den andra rektangeln. När jag nu ska beräkna arean:
Då blir det basen gånger höjden: i detta fall 1 (basen) gånger höjden (2) - 1 gånger 2= 2
Omkretsen blir då 1+1-2-2= 6

Men nu frågas det ju efter den maximala arean? Hur ska jag tänka då?
Du har rätt i att rektangelns area är basen gånger höjden.
Är du med på att om övre högra hörnet har koordinaterna (x: y) så är basen x och höjden y?
Ja precis, Basen x är 1 och höjden y är 2.
Men hur kan jag räkna fram den maximala arean?
Nej, det stämmer inte. Jag tror att du skall rita en gång till och lägga in bilden här igen. Ett hörn skall ligga i origo, ett hörn skall ligga i punkten (x,0), ett hörn skall ligga i punkten (x,y) och ett hörn skall ligga i punkten (0,y) där y=6-4x d v s hörnet (x,y) skall ligga på linjen y=6-4x.

Stämmer detta nu?

anonymousnina skrev:

Stämmer detta nu?

Ja, i stort sett. Uppställningen, uträkningen och det numeriska värdet i svaret är rätt.

Jag har ett par kommentarer och en fråga.

Du har gjort ett slarvfel när du ställde upp ekvationen. Det ska vara 6 = 8x men du skrev 6x = 8x.
Du bör motivera att x = 0,75 ger maximal och inte minimal area.
Enheten i svaret ska vara a.e. dvs areaenheter, inte cm^2.

Slutligen frågan: Förstår du lösningen helt och hållet, dvs varför arean uttrycks på det sättet, varför du deriverar och sätter derivatan lika med 0 och så vidare?

Yngve skrev:
anonymousnina skrev:
Stämmer detta nu?
Ja, i stort sett. Uppställningen, uträkningen och det numeriska värdet i svaret är rätt.
Jag har ett par kommentarer och en fråga.
Du har gjort ett slarvfel när du ställde upp ekvationen. Det ska vara 6 = 8x men du skrev 6x = 8x.
Du bör motivera att x = 0,75 ger maximal och inte minimal area.
Enheten i svaret ska vara a.e. dvs areaenheter, inte cm^2.
Slutligen frågan: Förstår du lösningen helt och hållet, dvs varför arean uttrycks på det sättet, varför du deriverar och sätter derivatan lika med 0 och så vidare?

Nej jag hänger inte helt med där. Jag hittade svaret på nätet. Jag förstår att rektangeln är där den ska vara då den uppfyller kraven i uppgiften vilket den andra rektangeln ej gjorde. Att man ska ta basen gånger höjden förstår jag också, men hur man kom fram till maximala arean vet jag inte.

Arean för en rektangel är basen gånger höjden. Basen i din rektangel är x och höjden är y=6-4x, så arean blir A(x)= xy = x(6-4x) = 6x-4x².

För att ta reda på var arean har sitt extremvärde, deriverar man areafunktionen - när arean är som störst (eller som minst) är derivatan av areafunktionen = A'(x) = 0.

Är du med så långt?

Smaragdalena skrev:
Arean för en rektangel är basen gånger höjden. Basen i din rektangel är x och höjden är y=6-4x, så arean blir A(x)= xy = x(6-4x) = 6x-4x².
För att ta reda på var arean har sitt extremvärde, deriverar man areafunktionen - när arean är som störst (eller som minst) är derivatan av areafunktionen = A'(x) = 0.
Är du med så långt?

Yes!

Kan du derivera funktionen A(x)=6x-4x² och lösa ekvationen A'(x)=0?

Smaragdalena skrev:
Kan du derivera funktionen A(x)=6x-4x² och lösa ekvationen A'(x)=0?

Jaa, nu förstår jag!! 😊👍 Tack alla för hjälpen!