Med hur många procent minskar jordens gravitationskraft?
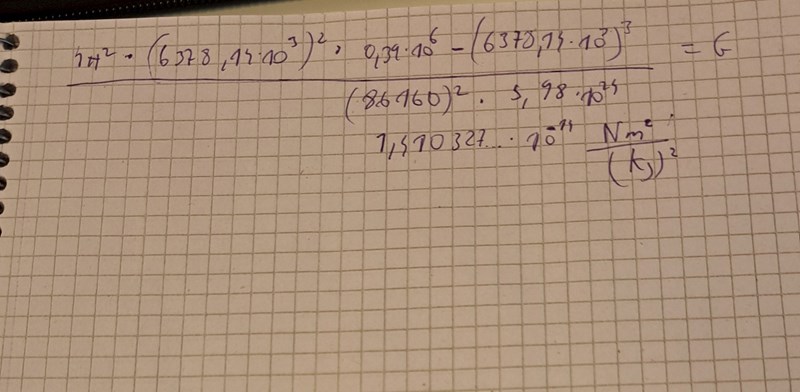
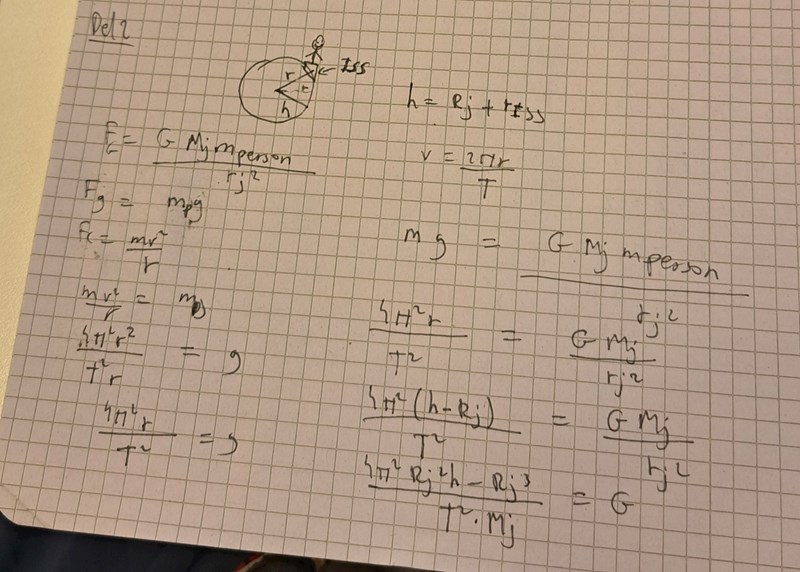
-1.jpg?width=800&upscale=false)
Hej!
Jag vet ej om man ska ta skillnaden och dividera med gamla värdet (i detta fall Konstanten G från formelsamlingen) för att få ut procent ?
Hur många procent längre från jordens centrum än vi var Marcus Wandt?
Förtydligande: svensken som var på ISS för några veckor sedan.
Pieter Kuiper skrev:Hur många procent längre från jordens centrum än vi var Marcus Wandt?
Jag förstår ej riktigt din fråga. Menar du hur många procent längre från jordens centrum är vi från astronauten Marcus Wandt?
Hur långt är vi från jordens centrum?
Marcus Wandt var 390 km högre upp.
Hur mycket längre ifrån jorden centrum är det uttryckt i procent?
Visa spoiler
Jordradien år
Pieter Kuiper skrev:Hur långt är vi från jordens centrum?
Marcus Wandt var 390 km högre upp.
Hur mycket längre ifrån jorden centrum är det uttryckt i procent?Visa spoiler
Jordradien år
Vad är fel med min uträkning? Jag använde ekvatorradie
destiny99 skrev:Jag använde ekvatorradie
Ok, samma sak.
Så samma fråga en tredje gång: hur mycket längre från jordens centrum är ISS, uttryckt i procent?
Pieter Kuiper skrev:destiny99 skrev:Jag använde ekvatorradie
Ok, samma sak.
Så samma fråga en tredje gång: hur mycket längre från jordens centrum är ISS, uttryckt i procent?
Det blir ju Re-h/Re?
Fjärde gång: hur många procent?
Pieter Kuiper skrev:Fjärde gång: hur många procent?
6%. Facit säger 11 % dock
destiny99 skrev:Pieter Kuiper skrev:Fjärde gång: hur många procent?
6%. Facit säger 11 % dock
Ja, eftersom gravitationen går som 1/r2.
Pieter Kuiper skrev:destiny99 skrev:Pieter Kuiper skrev:Fjärde gång: hur många procent?
6%. Facit säger 11 % dock
Ja, eftersom gravitationen går som 1/r2.
Men vad är felet med mitt sätt att lösa? Jag ändrade h+Rj nu. Jag skrev fel tidigare.

destiny99 skrev:
Men vad är felet med mitt sätt att lösa?
Att man inte kan följa vad du gör.
Att det har en mycket lägre sannolikhet att räkna rätt.
Att det kräver elektronisk räknare.
Att det är mycket mer jobb.
Pieter Kuiper skrev:destiny99 skrev:
Men vad är felet med mitt sätt att lösa?Att man inte kan följa vad du gör.
Att det har en mycket lägre sannolikhet att räkna rätt.
Att det kräver elektronisk räknare.
Att det är mycket mer jobb.
Jag började med ställa upp mg= GMjmperson/r^2 Sen visste jag att Fc=mperson*g pga det är cirkulär rörelse och hittade uttryck för g och använde den för att få ut vad G är för något. Sen drog jag bort givna G ur formelsamling från vårt nya G och dividerade med gamla G för att få i procent. Om denna metod är felaktig kommer jag ej på annan metod.

Hur då?
Jag började med ställa upp mg= GMjmperson/r^2
Vad betydet m, g, G, M, j, m, (samma som tidigare?)p, e, r, s, o, n, r?
Smaragdalena skrev:Jag började med ställa upp mg= GMjmperson/r^2
Vad betydet m, g, G, M, j, m, (samma som tidigare?)p, e, r, s, o, n, r?
m är massan för personen (du enligt texten). Lilla g är tyngdaccelerationen. G är gravitationskonstanten. Mj= Jordens massa.
Pieter Kuiper skrev:
Hur då?
Ja jag vet facit sa emot mig med 11% som svar.
destiny99 skrev:Pieter Kuiper skrev:
Hur då?Ja jag vet facit sa emot mig med 11% som svar.
Enligt standard procenträkning innebär en faktor 0,9997 en minskning med 0,03 %.
Pieter Kuiper skrev:destiny99 skrev:Pieter Kuiper skrev:
Hur då?Ja jag vet facit sa emot mig med 11% som svar.
Enligt standard procenträkning innebär en faktor 0,9997 en minskning med 0,03 %.
Jaa men det är fortfarande fel. Vilken metod skall man ha använt här då?
Enligt Newtons grav lag är
F = G*m1*m2/r2
Där G är en konstant
m1 är ena kroppens massa
m2 är den andra kroppens massa
r är avståndet mellan kropparnas masscentrum
Om vi flyttar oss från jordytan 390 km uppåt så ändras bara r, allt annat är oförändrat
Därför kan vi förenkla och säga att
Fjorden = K/r2
Där K är en konstant som består av G och de två massorna och r är jordradien
390 km upp gäller att kraften är
F390kmupp = K/(r*b)2
där b är avståndsförändringens förändringsfaktor, i vårt fall 1,06, om jordradien är 6400 km. Vi har kommit 6% längre från jordens masscentrum.
För att få den procentuella kraftminskningen
(Fjord-F390kmupp)/Fjord =
1- F390kmupp/Fjord =
= = 11%
Ture skrev:Enligt Newtons grav lag är
F = G*m1*m2/r2
Där G är en konstant
m1 är ena kroppens massa
m2 är den andra kroppens massa
r är avståndet mellan kropparnas masscentrumOm vi flyttar oss från jordytan 390 km uppåt så ändras bara r, allt annat är oförändrat
Därför kan vi förenkla och säga att
Fjorden = K/r2
Där K är en konstant som består av G och de två massorna och r är jordradien
390 km upp gäller att kraften är
F390kmupp = K/(r*b)2
där b är avståndsförändringens förändringsfaktor, i vårt fall 1,06, om jordradien är 6400 km. Vi har kommit 6% längre från jordens masscentrum.
För att få den procentuella kraftminskningen
(Fjord-F390kmupp)/Fjord =
1- F390kmupp/Fjord =
= = 11%
Facit gjorde såhär. Varför skrev de R+h i den andra uttrycket och vad menar de med det? Jag vet att h= Re(jordens ekvatorradie)-Riss(radien till internationella rymdstationen)

destiny99 skrev:
Facit gjorde såhär. Varför skrev de R+h i den andra uttrycket och vad menar de med det? Jag vet att h= Re(jordens ekvatorradie)-Riss(radien till internationella rymdstationen)
R+h är avståndet från jordens masscentrum till rymdstationen.
Facit har valt att räkna med avståndet i meter, medan Pieters lösning, som jag slutförde, räknar på den procentuella förändringen.
Båda metoderna ger samma svar, vilken man väljer är upp till var och en. Jag tycker att den lösning som Pieter skissade på är att föredra eftersom det blir enklare beräkningar, och därför mindre sannolikt att man gör fel.
Jag gissar att facits lösning är den som gymnasieelever tänker på i första hand, medan Pieters är mer ingenjörsmässig.
Den viktigaste lärdomen från båda lösningarna är att inte sätta in en massa siffror direkt och räkna på, utan vänta med siffrorna så länge det går. Ofta kan man förkorta bort en massa parametrar.
Ture skrev:destiny99 skrev:Facit gjorde såhär. Varför skrev de R+h i den andra uttrycket och vad menar de med det? Jag vet att h= Re(jordens ekvatorradie)-Riss(radien till internationella rymdstationen)
R+h är avståndet från jordens masscentrum till rymdstationen.
Facit har valt att räkna med avståndet i meter, medan Pieters lösning, som jag slutförde, räknar på den procentuella förändringen.
Båda metoderna ger samma svar, vilken man väljer är upp till var och en. Jag tycker att den lösning som Pieter skissade på är att föredra eftersom det blir enklare beräkningar, och därför mindre sannolikt att man gör fel.
Jag gissar att facits lösning är den som gymnasieelever tänker på i första hand, medan Pieters är mer ingenjörsmässig.
Den viktigaste lärdomen från båda lösningarna är att inte sätta in en massa siffror direkt och räkna på, utan vänta med siffrorna så länge det går. Ofta kan man förkorta bort en massa parametrar.
Jaha okej. Då är jag med! Ja jag föredrar facits lösning vilket var lätt att hänga med och det var ungefär så jag tänkte men jag använde felaktig formel för att räkna ut när personen ska röra sig upp över ekvatorn.
Ture skrev:Jag gissar att facits lösning är den som gymnasieelever tänker på i första hand,
Det är vad de lär sig, och det är lite trist.
Facit gör väldigt omständigt. Och bör förstås skrivas som innan man använder miniräknaren.







