Medelhastighet på en pendelkula
Hej! Jag höll på med denna uppgift:
"En pendel består av en liten blykula som är upphängd i en mycket lätt tråd med längden . Pendeln försätts i svängningar med maximala utslagsvinkeln . Visa att pendelkulans medelhastighet från ena vändläget till det andra är mycket nära "
Jag tog en rätt så matematisk väg och verkade inte leda fram till dit man ska.
Min ide är att hastigheten kommer bero av vinkeln, så om jag hittar en funktion som beskriver hastigheten som en funktion av vinkeln och beräknar medelvärdet på denna funktion så har vi svaret.
Vi kan se pendeln såhär: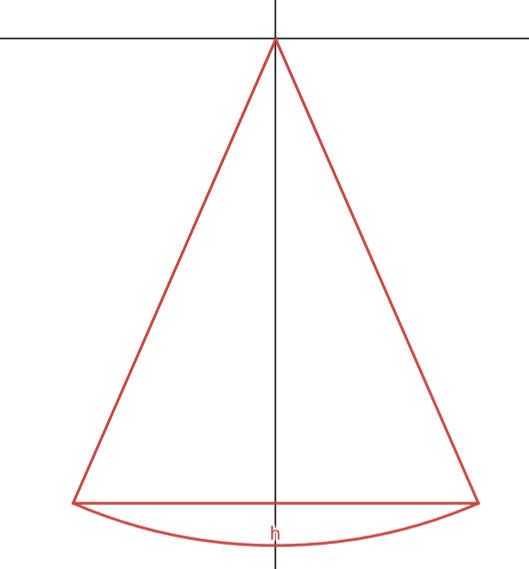
Vid gränserna har kulan hastigheten 0. Då är all energi lägesenergi. Om vi låter höjden "0" vara längst ned i mitten får vi med trigonometri att när kulan är längst ut till vänster är höjden
Då är energin där
Eftersom energi är konstant kommer detta vara den totala energin genom rörelsen.
På liknande sätt kan vi beräkna höjden för en viss vinkel på pendeln.
Med trigonometri får vi att . Då får vi att lägesenergin för en viss punkt på pendeln är
Detta ger oss att rörelseenergin vid en viss vinkel är
Eftersom har vi
Då är det bara att finna medelvärdet på denna funktion när går mellan 0 och ()
Medelvärdet över ett intervall på en funktion är integralen över intervallet / längden. Så:
Problemet är att denna integral inte har en elementär antiderivata och sedan är det numeriska värdet inte ens särskilt nära .
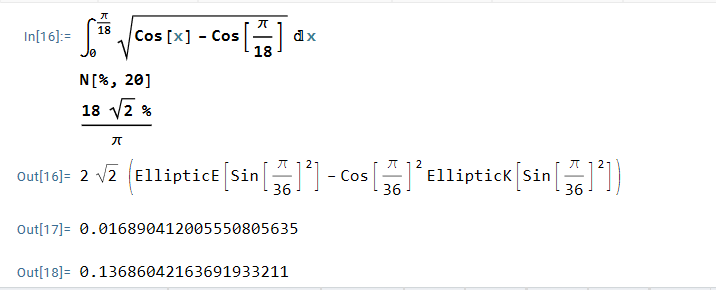
Jag skulle kunna ersätta med och beräkna integralen på det sättet. Men jag tror att man bara ska göra någon förenkling eller avrundning tidigare. Vart?
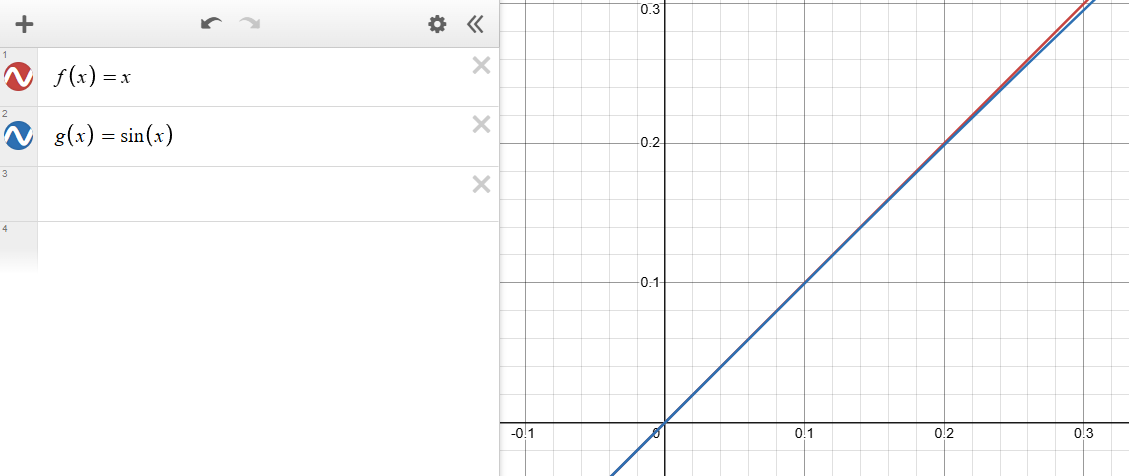
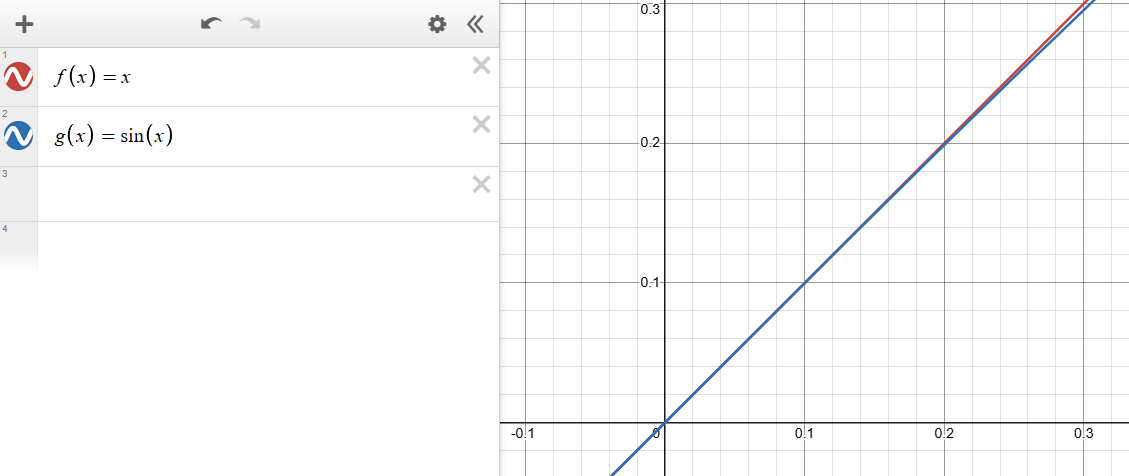
Jag gissar det är denna förenkling du söker, för små vinklar.
Det är kanske bara meningen att ta medelhastigheten som ?
Tiden är en halv period och för denna vinkel fortfarande rimligt oberoende av vinkel.
sictransit skrev:Jag gissar det är denna förenkling du söker, för små vinklar.
Jag använder ju cosinus och då finns approximationen för små vinklar, fortfarande blir integralen knepig (elementär, men knepig)

Dessa är faktiskt rätt nära, ja
Pieter Kuiper skrev:Det är kanske bara meningen att ta medelhastigheten som ?
Tiden är en halv period och för denna vinkel fortfarande rimligt oberoende av vinkel.
Hur tänker du då att man beräknar sträckan? Jag tänker att min integral är sträckan eftersom jag integrerar en hastighetsfunktion. Använda för mycket små vinklar?
AlexMu skrev:Pieter Kuiper skrev:Det är kanske bara meningen att ta medelhastigheten som ?
Tiden är en halv period och för denna vinkel fortfarande rimligt oberoende av vinkel.Hur tänker du då att man beräknar sträckan? Jag tänker att min integral är sträckan eftersom jag integrerar en hastighetsfunktion
Sträckan är cirkelsegment över 20 grader. Alltså .
Pieter Kuiper skrev:AlexMu skrev:Pieter Kuiper skrev:Det är kanske bara meningen att ta medelhastigheten som ?
Tiden är en halv period och för denna vinkel fortfarande rimligt oberoende av vinkel.Hur tänker du då att man beräknar sträckan? Jag tänker att min integral är sträckan eftersom jag integrerar en hastighetsfunktion
Sträckan är cirkelsegment över 20 grader. Alltså .
Ja, du har rätt.
Vi har att svängningstiden är
Så, halva svängningstiden från ena sidan till den andra är
Streckan, som du sade är då
Så,
Tack!