Medelkraft vinkelrätt mot PQ i ett magnetfält
Ett homogent vertiklat magnetfält har ett rektangulärt tvärsnitt PQRS, se fig. En horisontell ström av elektroner kommer in i fältet vid A, vinkelrätt mot PQ med farten . De böjs och lämnar åter fältet vinkelrätt mot PQ vid B. Avståndet AB är 0,120 m. Elektronstålen befinner sig hela tiden i vakuum.
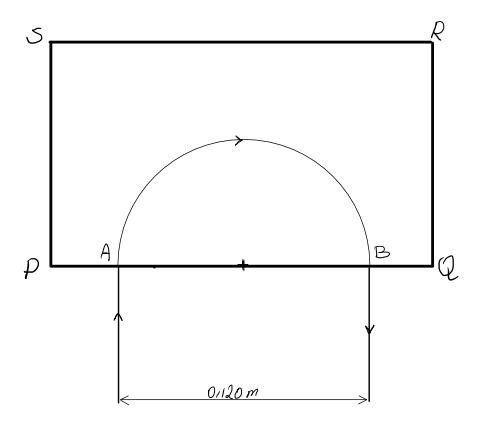
a) Beräkna magnetiska flödestätheten till storlek och riktning.
b)Hur stor medelkraft vinkelrätt mot PQ verkar på elektronerna under den tid de rör sig i magnetfältet?
Bortse från jordmagnetiska fältet och gravitationen.
Jag har fått rätt svar på båda delarna. För första delen fick jag B=0,59 mT(in i planet) och på andra delen fick jag tips från facit om att jag ska använda mig av impulslagen. Så här har jag gjort:
Och det är korrekt. Men frågan är varför ska man använda impulslagen för att räkna medelkraften vinkelrätt mot PQ?
Är det för att den vinkelräta kraften är hela tiden vinkelrätt mot PQ och eftersom vi vet hur stor den vertikala komposanten av hastigheten i början och slutet av elektronens rörelse i magnetfältet är så får vi använda impulslagen?
Du måste använda impulslagen för att kraften är en vektor vilken byter riktning enligt att måla upp en halvcirkel. Det finns andra sätt att göra på men de är på universitetsnivå.
Ebola skrev:Hur kan magnetfältet vara konstant om farten ändras? Enligt sin uträkning är farten dubbelt så stor när den åker ut vid B.
Farten har inte ändrats. Det är delta v som blir dubbel så stor som den konstanta hastigheten.
Marx skrev:Farten har inte ändrats. Det är delta v som blir dubbel så stor som den konstanta hastigheten.
Mm, jag såg det. Se mitt redigerade svar. Något som saknas i din relation förövrigt är att impulslagen ger just medelkraften. Det ska alltså vara ett streck ovanför kraften. Impulslagen är egentligen en tidsintegral.
Ebola skrev:Marx skrev:Farten har inte ändrats. Det är delta v som blir dubbel så stor som den konstanta hastigheten.
Mm, jag såg det. Se mitt redigerade svar. Något som saknas i din relation förövrigt är att impulslagen ger just medelkraften. Det ska alltså vara ett streck ovanför kraften. Impulslagen är egentligen en tidsintegral.
Ja, det är sant. Den egentliga formeln är . Men nu blir jag nyfiken! Du har skrivit att det finns andra metoder också för att räkna ut medelkraften, kan du skriva vilka? Tack!
Jag kan skriva en av metoderna då övriga kommer sannolikt enbart vara ett glyfpussel och denna är på gränsen. Vi söker medelkraften vinkelrät till linjen PQ vilket betyder att vi söker medelkraften som pekar rakt ned. Om vi tittar på en godtycklig punkt mellan A och B har vi:
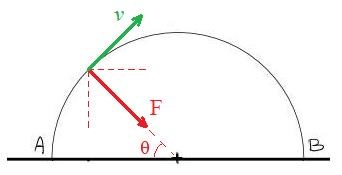
Vi ser alltså att komponenten av kraften som pekar rakt ned är i punkten:
Där vi har att storleken på kraften är . Vi får nu medelvärdet från en integral:
Vi har alltså här summerat komponenterna som pekar nedåt vid varje punkt då vinkeln varierar från till och sedan delat med längden på området (halva cirkelns omkrets). Om vi stoppar in allting och beräknar integralen får vi:
Ebola skrev:Jag kan skriva en av metoderna då övriga kommer sannolikt enbart vara ett glyfpussel och denna är på gränsen. Vi söker medelkraften vinkelrät till linjen PQ vilket betyder att vi söker medelkraften som pekar rakt ned. Om vi tittar på en godtycklig punkt mellan A och B har vi:
Vi ser alltså att komponenten av kraften som pekar rakt ned är i punkten:
Där vi har att storleken på kraften är . Vi får nu medelvärdet från en integral:
Vi har alltså här summerat komponenterna som pekar nedåt vid varje punkt då vinkeln varierar från till och sedan delat med längden på området (halva cirkelns omkrets). Om vi stoppar in allting och beräknar integralen får vi:
Det här var inte så svårt att förstå! Både impulslagen och den integral som du har använt dig av leder till samma resultat, alltså: .
Du har använt dig av polär integral längs den cirkulära banan och sedan delat det med halva cirkelns omkrets för att få fram den genomsnittliga vertikala komponenten av kraften.



