Medelskjuvspänning skruvförband
Hej! Jag förstår inte riktigt vad jag letar efter i denna uppgift,
F=t*A
A=r^2*pi =》 5^2*pi=78,54mm^2
A=110 =L
Två skruvar = 78,54 mm^2
80N/mm^2
F=80*78.54= 6283,2 N

Justerade din rubrik så att det inte ser ut som en dubbelpost /Smaragdalena, moderator
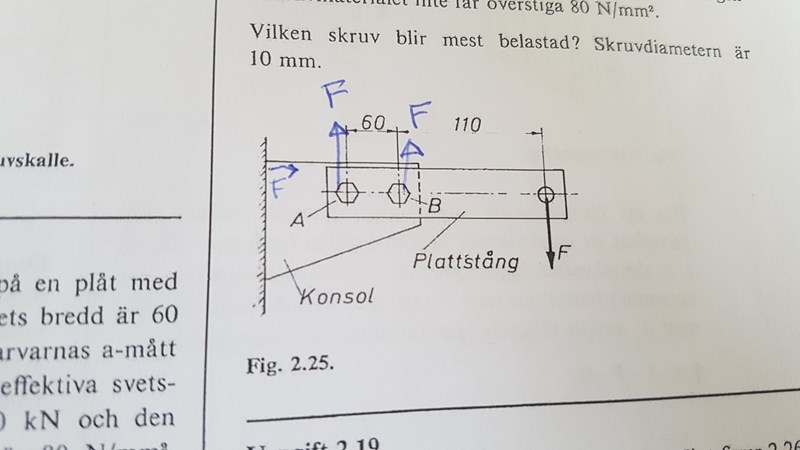
Börja med att rita in krafterna som verkar på vardera skruven. Eftersom man frågar "Vilken av skruvarna blir mest belastad?" kan man inse (eller åtminstone gissa) att belastningen på de båda är olika.
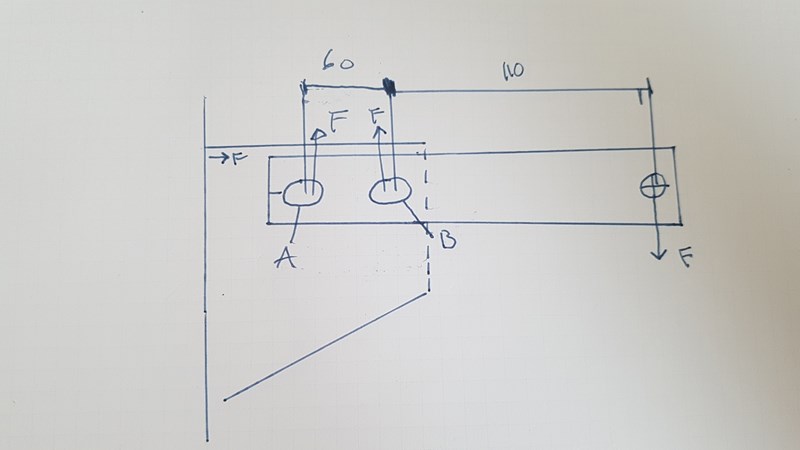
Då får vi två krafter som verkar uppåt av skeven om jag inte har fel , för att vi har en kraft som är riktad nedåt
Har du ritat? Jag förstår inte vad du menar - lägg in din bild här så att vi vet att vi pratar om samma sak.
Hur beräknar du respektive ? De är inte lika.
B borde vara större, men jag har denna formel F=t*A men har ingen aning hur jag gör härnäst
A=5^2*pi=78.54mm^2
t=80n/mm^2
80*78,54=6283.2N
mesper skrev:B borde vara större, men jag har denna formel F=t*A men har ingen aning hur jag gör härnäst
Hur resonerar du? (Jag säger inte att det är rätt eller fel, jag bara påpekar att det saknas en motivering till varför.)
Pågrund av att kraften B(uppåt) ligger närmare kraften neråt F som kommer då ha en större inverkan på själva kraften.
mesper skrev:Pågrund av att kraften B(uppåt) ligger närmare kraften neråt F som kommer då ha en större inverkan på själva kraften.
Nu förstår jag inte alls. Om du tänker på hävstänger, så ger en längre hävarm ett större moment om kraften är densamma.
Vad menar du med "själva kraften"? Var har du den i din skiss?
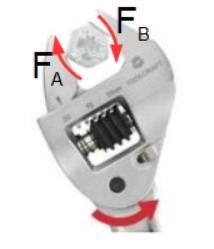
Jag tycker att denna uppgift delvis påminner om detta:
 Dvs. man ska nog tänka sig ett (imaginärt) rotationscentrum mitt emellan bultarna (skruvarna).
Dvs. man ska nog tänka sig ett (imaginärt) rotationscentrum mitt emellan bultarna (skruvarna).
I så fall är skjuvkrafterna på båda bultarna (skruvarna) lika.
Affe Jkpg skrev:Jag tycker att denna uppgift delvis påminner om detta:
Dvs. man ska nog tänka sig ett (imaginärt) rotationscentrum mitt emellan bultarna (skruvarna).
I så fall är skjuvkrafterna på båda bultarna (skruvarna) lika.
I så fall...varje skruv mottar halva momentet från F och vi får kraften på varje skruv:
Jag ska alltså räkna ut momentet för kraften i skruvarna ?
Där 30 är längden mellan dessa två skruvar* kraften på skruven = 1/2 140(längden) * kraften neråt
Vi räknar ut ekvationen
3*fskruv=7*F
Jag måste erkänna att jag fortfarande är snurrig
Jag tänker mig en annan lösning än Affes. Plattstången kommer att försöka vrida sig kring skruven B, så . Använd medelskjuvspänningen för att beräkna och därefter .
EDIT: Nu bortser jag från plattstångens massa.
Smaragdalena skrev:Jag tänker mig en annan lösning än Affes. Plattstången kommer att försöka vrida sig kring skruven B, så . Använd medelskjuvspänningen för att beräkna och därefter .
EDIT: Nu bortser jag från plattstångens massa.
Påstår du då att momentet och skjuvkraften på skruven B är noll?
mesper skrev:Jag ska alltså räkna ut momentet för kraften i skruvarna ?
Där 30 är längden mellan dessa två skruvar* kraften på skruven = 1/2 140(längden) * kraften neråt
Vi räknar ut ekvationen
3*fskruv=7*F
Jag måste erkänna att jag fortfarande är snurrig
Kan du rita momentkrafterna, när vridningscentrum ligger mitt emellan skruvarna?
Momentet på B är 0, eftersom plattstången vrider sig runt skruven B.
Varför skulle vridcentrum ligga mitt emellan skruvarna? Vad finns det där som plattstången skulle kunna vrida sig runt? Vad skulle hända om vi tar bort lasten, om ditt resonemang stämmer?
Fa=t*A=》80*60=4800N
F=t*A》80*110=8800N
Fa-F=》 8800N-4800=4000 N
Du har inte tagit hänsyn till skruvens area. Du har räknat med att arean är men det står i uppgiften att skruvdiameterna är 10 mm.
Smaragdalena skrev:Momentet på B är 0, eftersom plattstången vrider sig runt skruven B.
Varför skulle vridcentrum ligga mitt emellan skruvarna? Vad finns det där som plattstången skulle kunna vrida sig runt? Vad skulle hända om vi tar bort lasten, om ditt resonemang stämmer?
Med ditt resonemang kan det väl lika gärna vrida sig runt skruven A?
Jag kompletterar min tidigare illustration om vad denna uppgift liknar:
A=5^2*pi=78,54
Fa=t*A =》 80*78.54 =4712.5 N
F=80*110÷8800N
8800-4712.5 N = 4088 N
Om momentet på någon av skruvarna A eller B skulle vara noll, kan man väl ta bort en av dom?
Affe jag skulle gärna vilja testa din metod men jag begriper mig inte vart jag ska börja ,Då jag kommer få olika krafter på a och b
I facit står det , skruven B blir mest belastad , 2.22 kN blir svaret, jag får svaret 2044 N
mesper skrev:I facit står det , skruven B blir mest belastad , 2.22 kN blir svaret, jag får svaret 2044 N
Då är det bara att konstatera att jag tänkte helt fel.
Affe Jkpg skrev:Affe Jkpg skrev:Jag tycker att denna uppgift delvis påminner om detta:
Dvs. man ska nog tänka sig ett (imaginärt) rotationscentrum mitt emellan bultarna (skruvarna).
I så fall är skjuvkrafterna på båda bultarna (skruvarna) lika.
I så fall...varje skruv mottar halva momentet från F och vi får kraften på varje skruv:
F= 3*78.54 / 7 = 33.66 N
mesper skrev:Affe Jkpg skrev:Affe Jkpg skrev:Jag tycker att denna uppgift delvis påminner om detta:
Dvs. man ska nog tänka sig ett (imaginärt) rotationscentrum mitt emellan bultarna (skruvarna).
I så fall är skjuvkrafterna på båda bultarna (skruvarna) lika.
I så fall...varje skruv mottar halva momentet från F och vi får kraften på varje skruv:
F= 3*78.54 / 7 = 33.66 N
Annars funderar jag på en annan lösning....:-)
2.7 kN blir för mycket enligt facit 😊 hur ser den andra lösningen ut ? Finns det någon bra video på nätet som du kan rekommendera gällande medelskjuvspänning?😊
Som jag läser uppgiften så är inte skruvskallarna försänkta i stålet, så själva hålen bör vara runda och inte sexkantiga. Det verkar då även rimligt att man kan bortse från alla moment som uppstår från att skruvskallarna "klämmer fast" stålet, om inte så måste vi ha friktionskoefficienten för att kunna veta hur stort detta "fastklämningsmoment" är.
Det som återstår för att lösa uppgiften borde då bara vara att ställa upp jämviktsekvationerna i vertikalled och sätta momentet lika med noll kring A eller B, då borde du få ut krafterna vid A och B. Sedan borde man kunna beräkna skjuvspänningen vid A och B och titta vilken punkt som ger störst värde, jämföra det med hållbarhetskriteriet och få fram något värde på F.
Slarvigt räknat fick jag 2.2 kN, vad är rätt svar?
emmynoether skrev:Som jag läser uppgiften så är inte skruvskallarna försänkta i stålet, så själva hålen bör vara runda och inte sexkantiga. Det verkar då även rimligt att man kan bortse från alla moment som uppstår från att skruvskallarna "klämmer fast" stålet, om inte så måste vi ha friktionskoefficienten för att kunna veta hur stort detta "fastklämningsmoment" är.
Det som återstår för att lösa uppgiften borde då bara vara att ställa upp jämviktsekvationerna i vertikalled och sätta momentet lika med noll kring A eller B, då borde du få ut krafterna vid A och B. Sedan borde man kunna beräkna skjuvspänningen vid A och B och titta vilken punkt som ger störst värde, jämföra det med hållbarhetskriteriet och få fram något värde på F.
Slarvigt räknat fick jag 2.2 kN, vad är rätt svar?
2,22 kN står det enligt facit och att skruven b blir mest belastad, Du får gärna visa lösningen jag känner mig lite snurrig av denna uppgift
Se till att dina svar hamnar utanför citatmarkeringen, det blirså rörigt annars! /Smaragdalena, moderator
Jo men visst, utgår från min tjusiga paintbild nedan
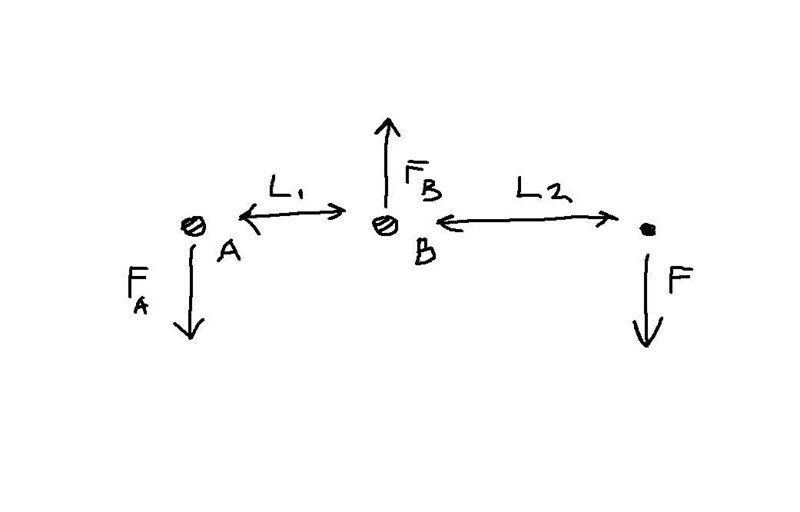
Jämvikt i vertikalled:
Momentjämvikt kring punkten A:
Utgår du från detta kan du lösa ut krafterna (får du göra själv) och borde få
och .
Skjuvningen ges som och vid punkten B är den som störst (eftersom arean är samma men kraften är större). Vi har ett värde för maximal skjuvning och vi har arean, så vi löser för kraften och får
EDIT: Ett generellt tips från mig är även att alltid rita en bild där du tar bort alla onödiga detaljer som inte behövs för uppgiften, som min paintbild ovan.
Tack ska du ha, mycket fin beskrivning! Jag får öva mer på detta.



.jpg?width=80&crop=0,0,80,80)
