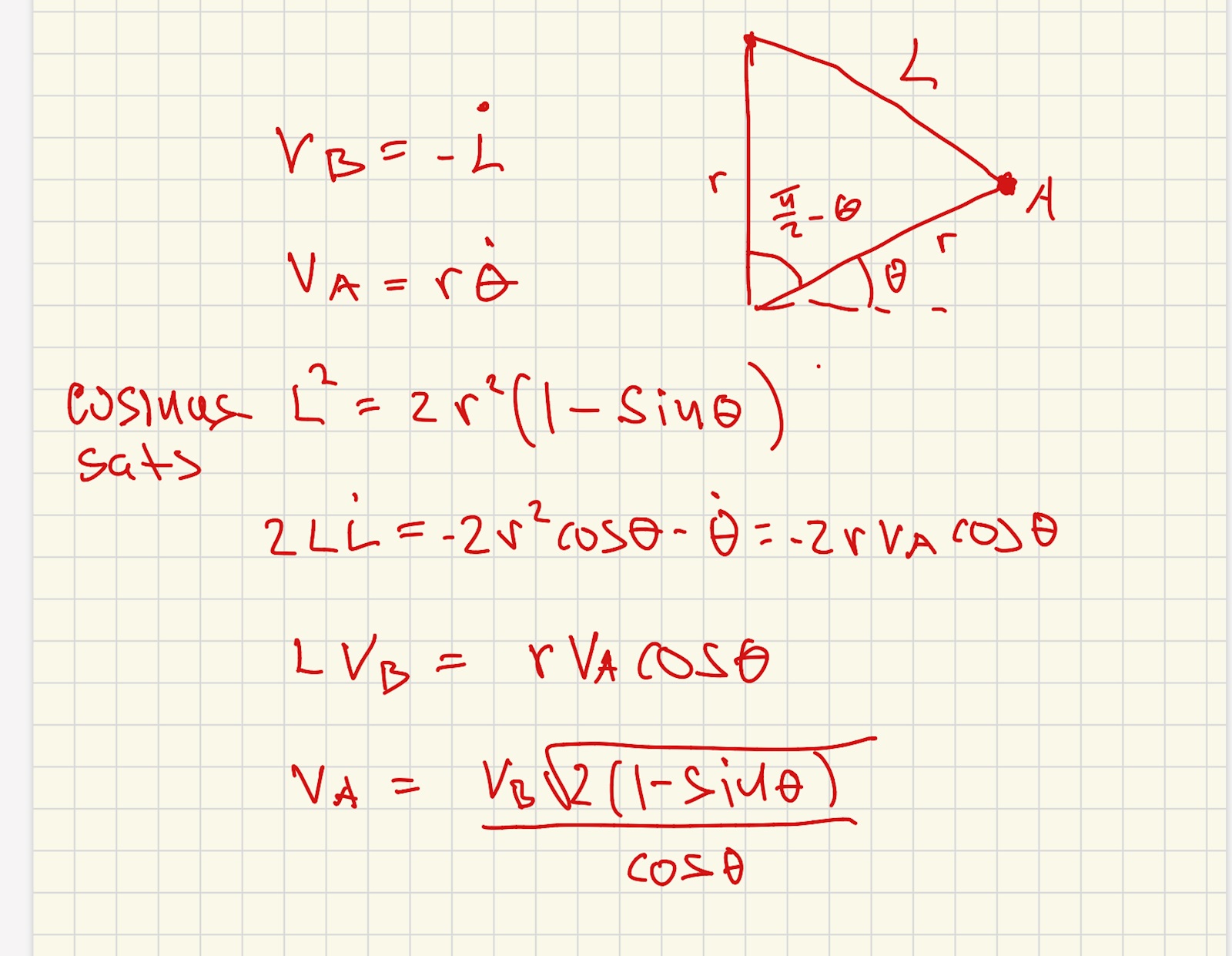Mekanik 1 - Dynamik (Tvångsvillkor och konstanta längd)

När B har hastigheten V_B har linan (och A) hastigheten V_A = V_B cos (alfa).

alfa fås genom att triangeln är likbent till (pi/4 - fi/2)

(Med reservation för felräkning och tankefel, men ändå)

hansa skrev:

När B har hastigheten V_B har linan (och A) hastigheten V_A = V_B cos (alfa).

alfa fås genom att triangeln är likbent till (pi/4 - fi/2)

(Med reservation för felräkning och tankefel, men ändå)

Hur vet du det och hur kunde du skriva om det på sådant sätt. Tog basically bort hela vänstersidan?

Ett försök.

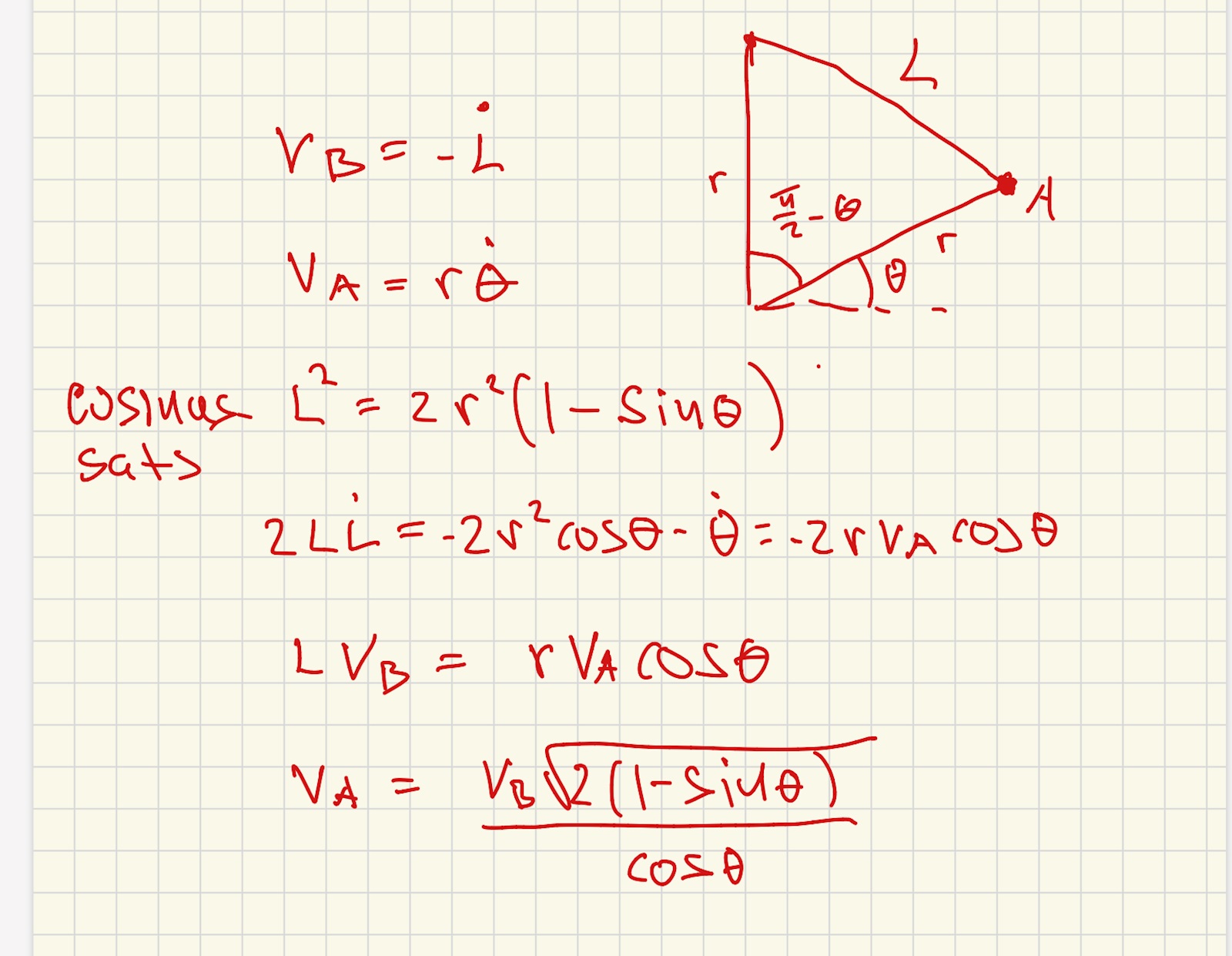
hansa skrev:

När B har hastigheten V_B har linan (och A) hastigheten V_A = V_B cos (alfa).

alfa fås genom att triangeln är likbent till (pi/4 - fi/2)

(Med reservation för felräkning och tankefel, men ändå)

Hmm, jag prövade v_A=v_B*cos($\frac{\pi }{4}-\frac{\theta }{2}$) men det blidde fel :/

Tror att Hansa blandat ihop v_A och v_B. Testa med 1/cos(pi/4-theta/2) istället.

PATENTERAMERA skrev:

Ett försök.

Det blidde rätt men venne om jag hänger med. Jag fick ju att v_A = $\stackrel{.}{L}$,  (fast som då var C). Hur visste du först och främst vilket tecken det skulle ha i sådana fall. 

Jaha vänta först så identifierar man vad det är för typ av rörelse, radien är konstant men den följer cirkelrörelse, ska man då använda sig av enhetsvektorer i polärt koordinatsystem. Dock ska inte v_A vara vinkelrät eller i alla fall e_$\theta$, för att det ska funka 

Jaha sen tas roten ur L² och så får då L och sen substituerar ut så försvinner r sedan.

Bara en grej jag fattar inte mitt-termen i fjärde ekvationen (-2r²cos$\theta$*$\stackrel{.}{\theta }$)

PATENTERAMERA skrev:

Tror att Hansa blandat ihop v_A och v_B. Testa med 1/cos(pi/4-theta/2) istället.

Ja det blev rätt!! Fattar fortfarande inte hur han kunde flytta hastigheten dit.

Sykey skrev:

Bara en grej jag fattar inte mitt-termen i fjärde ekvationen (-2r²cos$\theta$*$\stackrel{.}{\theta }$)

Man har deriverat raden ovanför.

DSykey skrev:

PATENTERAMERA skrev:

Ett försök.

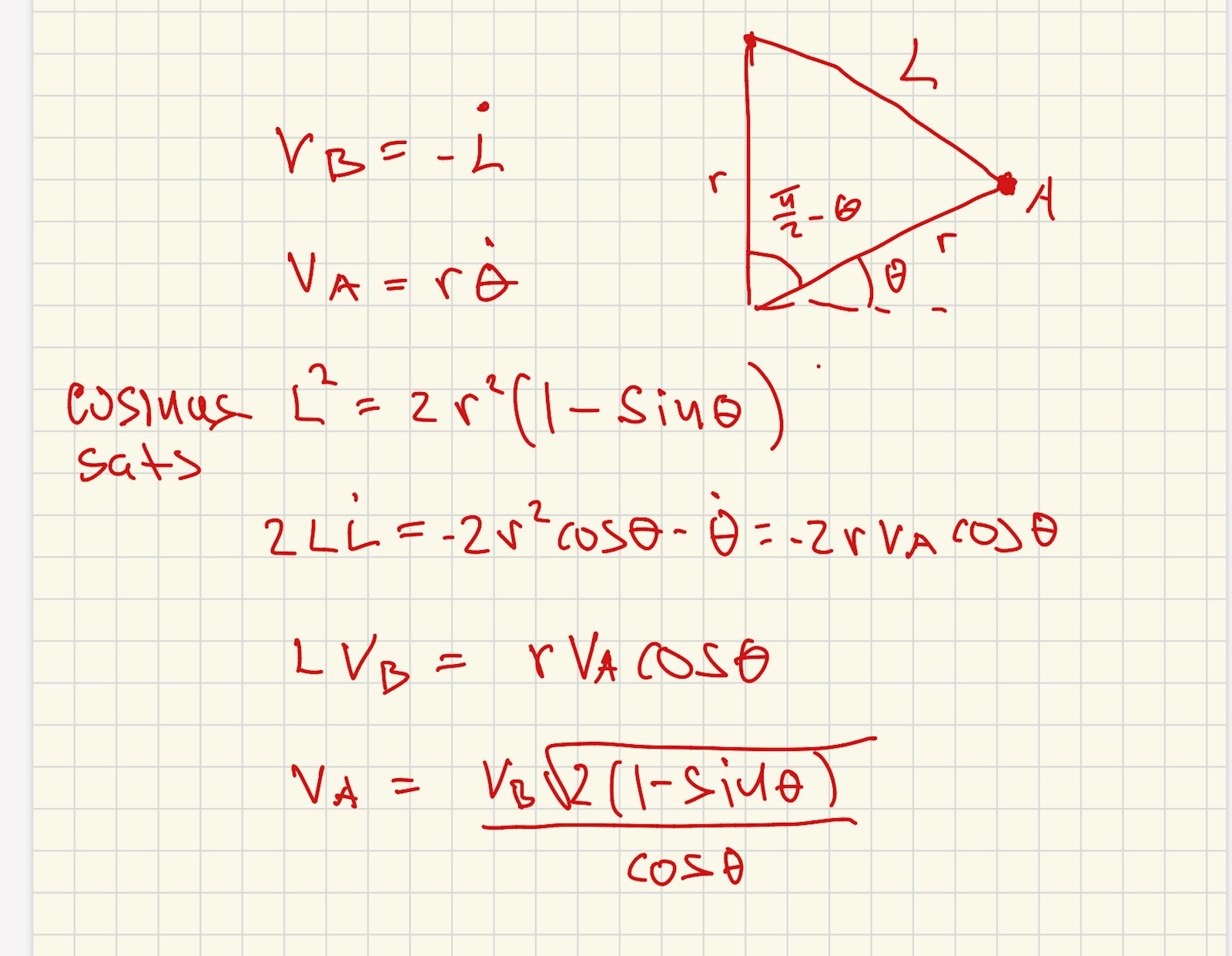
Det blidde rätt men venne om jag hänger med. Jag fick ju att v_A = $\stackrel{.}{L}$,  (fast som då var C). Hur visste du först och främst vilket tecken det skulle ha i sådana fall.  Nja, om B rör sig ner ett litet stycke så minskar L med motsvarande längd. V_B = -dL/dt.

Jaha vänta först så identifierar man vad det är för typ av rörelse, radien är konstant men den följer cirkelrörelse, ska man då använda sig av enhetsvektorer i polärt koordinatsystem. Dock ska inte v_A vara vinkelrät eller i alla fall e_$\theta$, för att det ska funka 

Jaha sen tas roten ur L² och så får då L och sen substituerar ut så försvinner r sedan.

Bara en grej jag fattar inte mitt-termen i fjärde ekvationen (-2r²cos$\theta$*$\stackrel{.}{\theta }$) Derivera båda sidor map t av det som cosinussatsen gav.

Jo jag hade förväxlat A och B (Nånting gammalt intuitivt trädde fram och placerade naturligt A till vänster om B, (ABC)). Då blir uttrycken samma  enligt beräkningarna ovan, med övergång till halva vinkeln.

Man kan fråga sig om kravet att svara i VB och teta innefattar teta/2 

Laguna skrev:

Sykey skrev:

Bara en grej jag fattar inte mitt-termen i fjärde ekvationen (-2r²cos$\theta$*$\stackrel{.}{\theta }$)

Man har deriverat raden ovanför.

Förstår fortfarande it 

Cosinussatsen ger

L² = 2r²$\left(1-\sin \theta \right)$ (1).

Derivera (1) map tiden.

HL. $\frac{d{L}^2}{dt}=\frac{d{L}^2}{dL}·\dot{L}=2L·\dot{L}$.

VL. $\frac{d\left(2r^2\left(1-\sin \theta \right)\right)}{dt}=2r^2\frac{d\left(1-\sin \theta \right)}{d\theta }\dot{\theta }= -2r^2\cos \theta ·\dot{\theta }$.

PATENTERAMERA skrev:

Cosinussatsen ger

L² = 2r²$\left(1-\sin \theta \right)$ (1).

Derivera (1) map tiden.

HL. $\frac{d{L}^2}{dt}=\frac{d{L}^2}{dL}·\dot{L}=2L·\dot{L}$.

VL. $\frac{d\left(2r^2\left(1-\sin \theta \right)\right)}{dt}=2r^2\frac{d\left(1-\sin \theta \right)}{d\theta }\dot{\theta }= -2r^2\cos \theta ·\dot{\theta }$.

Jaha du tänker så på sista, 2r² är en konstant så du bryter ut den, du använder kedjeregeln så du får $\frac{d}{d\theta }*\frac{d\theta }{dt} där \stackrel{.}{\theta } =\frac{d\theta }{dt}$, och därför kan du göra det m.a.p vinkeln. Ah nu make:ar det sense.

Men fortfarande så fattar jag inte hur ni båda två kunde flytta hastigheten från var den var, till höger, det var det jag mestadels inte hängde med på. Liksom hur visste ni båda två?

Menar du hur man kommer från andra ledet till det tredje? Det tittade jag inte på, men du har från tidigare att v_A = r theta-prick.

(jag vet inte hur man prickar thetor just nu.)

Laguna skrev:

Menar du hur man kommer från andra ledet till det tredje? Det tittade jag inte på, men du har från tidigare att v_A = r theta-prick.

(jag vet inte hur man prickar thetor just nu.)

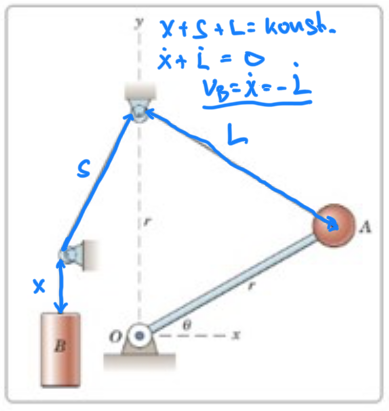
Näh men kolla på Hansas bild och kolla på min original bild på uppgiften. Kolla var hastigheten v_B är i uppgiften och kolla hur Hansa förflyttar den på något mirakel upp till punkten A. Liksom hur kan man koppla det.

Kolla också på Patenterameras beräkning, hur visste hen att v_B = -L (tecken inklusive) och att v_A = r$\stackrel{.}{\theta }$? Resten är beräkningar. Jag fattar det bara inte.

Klart?

PATENTERAMERA skrev:

Klart?

Bästa förklaringen jag sett för det är så sant. Hur var det med v_A då? Jag trodde det endast var lika med r$\stackrel{.}{\theta }$ då den var vinkelrät med radien, men det är ju v_a inte garanterat att vara. Hur tänkte Hansa istället annars?

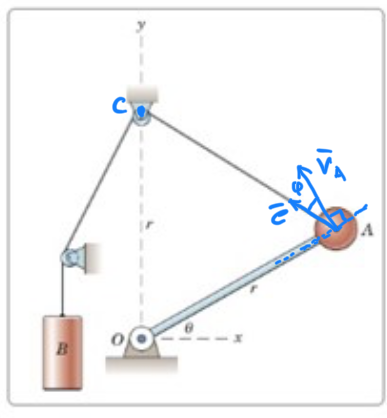A:s hastighetsvektor ${\overrightarrow{v}}_A$ är vinkelrät mot radien (vektorn $\overrightarrow{OA}$).

Om vi lägger in en enhetsvektor $\overrightarrow{e}$ längs linan (se figur) så gäller det (försök att visa det) att v_B = $\overrightarrow{e}·{\overrightarrow{v}}_A=v_A\cos \phi$. Dvs vi kan se v_B som projektionen av ${\overrightarrow{v}}_A$ i linans riktning. Hansa räknar fram vad $\phi$ är utifrån en betraktelse av geometrin.

Tillägg: 28 jan 2026 18:54

Obs hansa kallar vinkeln $\phi$ för $\alpha$.

PATENTERAMERA skrev:

A:s hastighetsvektor ${\overrightarrow{v}}_A$ är vinkelrät mot radien (vektorn $\overrightarrow{OA}$).

Om vi lägger in en enhetsvektor $\overrightarrow{e}$ längs linan (se figur) så gäller det (försök att visa det) att v_B = $\overrightarrow{e}·{\overrightarrow{v}}_A=v_A\cos \phi$. Dvs vi kan se v_B som projektionen av ${\overrightarrow{v}}_A$ i linans riktning. Hansa räknar fram vad $\phi$ är utifrån en betraktelse av geometrin.

---

Tillägg: 28 jan 2026 18:54

Obs hansa kallar vinkeln $\phi$ för $\alpha$.

Kunde ej bevisa:

Kan inte vara genom skalärprodukt, vektorprodukt.

Kanske projektion eller geometri

Mitt försök/tankesätt:

Att v_B är projektionen kan vi inte bara använda det du gjorde innan eftersom det anger L:s förändringshastighet (vilket då var v_B). 

Asså matten checks out men någonting känns ändå konstigt med intuitivt. v_B är ju riktad rakt neråt no? Alltså är v_B positiv, om vi använder din formel så är $\stackrel{.}{L}=-v_B$, och kom ihåg att v_B var riktad neråt, ah vänta jag insåg nyss en sak. Det är INTE VEKTORER så det säger ingenting om riktning, (wait a min, hastighet är en vektor dock inte en skalär), bara hur snabbt längden förändras per sekund.

Edit: Jag prövade det och jag kunde inte få till det vad det gällde tecknet vB= (-vB)*e. Min förklaring till att detta hade funkat är att förändringshastigheten L.är en storlek och om den är negativ och vi VET att vikten DRAR ner repet så repet går bara ett håll så är den RIKTNINGEN/HÅLLET negativt och därmed så är enhetsvektorn också negativ. Man brukar väl ändå säga typ så om system som inte är högerriktade?

Ja då är min enda förklaring denna v_B=-vB*e-, som jag inte kan förklara.

Titta på vektorn $\overrightarrow{CA}$. Det gäller då att

$L^2={\left|\overrightarrow{CA}\right|}^2=\overrightarrow{CA}·\overrightarrow{CA}$. Derivera detta map t.

$2L\dot{L}=2\overrightarrow{CA}·\frac{d\overrightarrow{CA}}{dt}$
$-L{v}_B=\overrightarrow{CA}·{\overrightarrow{v}}_A$

$v_B=\frac{-\overrightarrow{CA}}{L}·{\overrightarrow{v}}_A$

Men $\frac{-\overrightarrow{CA}}{L}=\frac{-\overrightarrow{CA}}{\left|\overrightarrow{CA}\right|}=\overrightarrow{e}$, så vi har att $v_B=\overrightarrow{e}·{\overrightarrow{v}}_A=v_A\cos \phi$.

PATENTERAMERA skrev:

Titta på vektorn $\overrightarrow{CA}$. Det gäller då att

$L^2={\left|\overrightarrow{CA}\right|}^2=\overrightarrow{CA}·\overrightarrow{CA}$. Derivera detta map t.

$2L\dot{L}=2\overrightarrow{CA}·\frac{d\overrightarrow{CA}}{dt}$
$-L{v}_B=\overrightarrow{CA}·{\overrightarrow{v}}_A$

$v_B=\frac{-\overrightarrow{CA}}{L}·{\overrightarrow{v}}_A$

Men $\frac{-\overrightarrow{CA}}{L}=\frac{-\overrightarrow{CA}}{\left|\overrightarrow{CA}\right|}=\overrightarrow{e}$, så vi har att $v_B=\overrightarrow{e}·{\overrightarrow{v}}_A=v_A\cos \phi$.

jaha det är det som är tricket, du använder formeln för normaliserad enhetsvektor. Intressant, okej och då inkluderade det negativa tecknet genom pure matematisk beräkning. Hade inte tänkt på det själv.