Mekanik 1 - Hitta Tyngdpunkt

Kan du hitta tyngdpunkten för en kvartscirkel?

Laguna skrev:

Kan du hitta tyngdpunkten för en kvartscirkel?

Nej, inte utan att jag kollar upp det, vilket jag inte får göra på tentor. Allt jag känner till är denna formeln för masscentrumsformeln 

$x=\frac{\int xdA}{A}$

för x koordinaten och vice versa för y koordinaten.

Ja, då kan du räkna ut det.

När du har den får du ta rektangeln minus kvartscirkeln, så att säga.

Kolla jag hänger knappt med. 

Arean av kvartscirkeln är $\frac{\mathrm{\pi }·{\mathrm{c}}^2}{4}$.  Jag kollar i boken hur de gör för cirkeln, de använder x-axeln som symmetriaxeln. Även om jag räknar ut tyngdpunkten för en kvartscirkel så är det inte det jag vill ha, jag vill ha tyngd punkten för c^2 - (pi*c^2)/4, alltså den lilla backen. Sen så måste jag ta till hänsyn att den inte börjar i origo heller. 

Jag hajar inte.

Känner igen den uppgiften. Kanske man kan göra på detta krångliga sätt som jag gjorde förra året. Densiteten ska vara /m^2. 

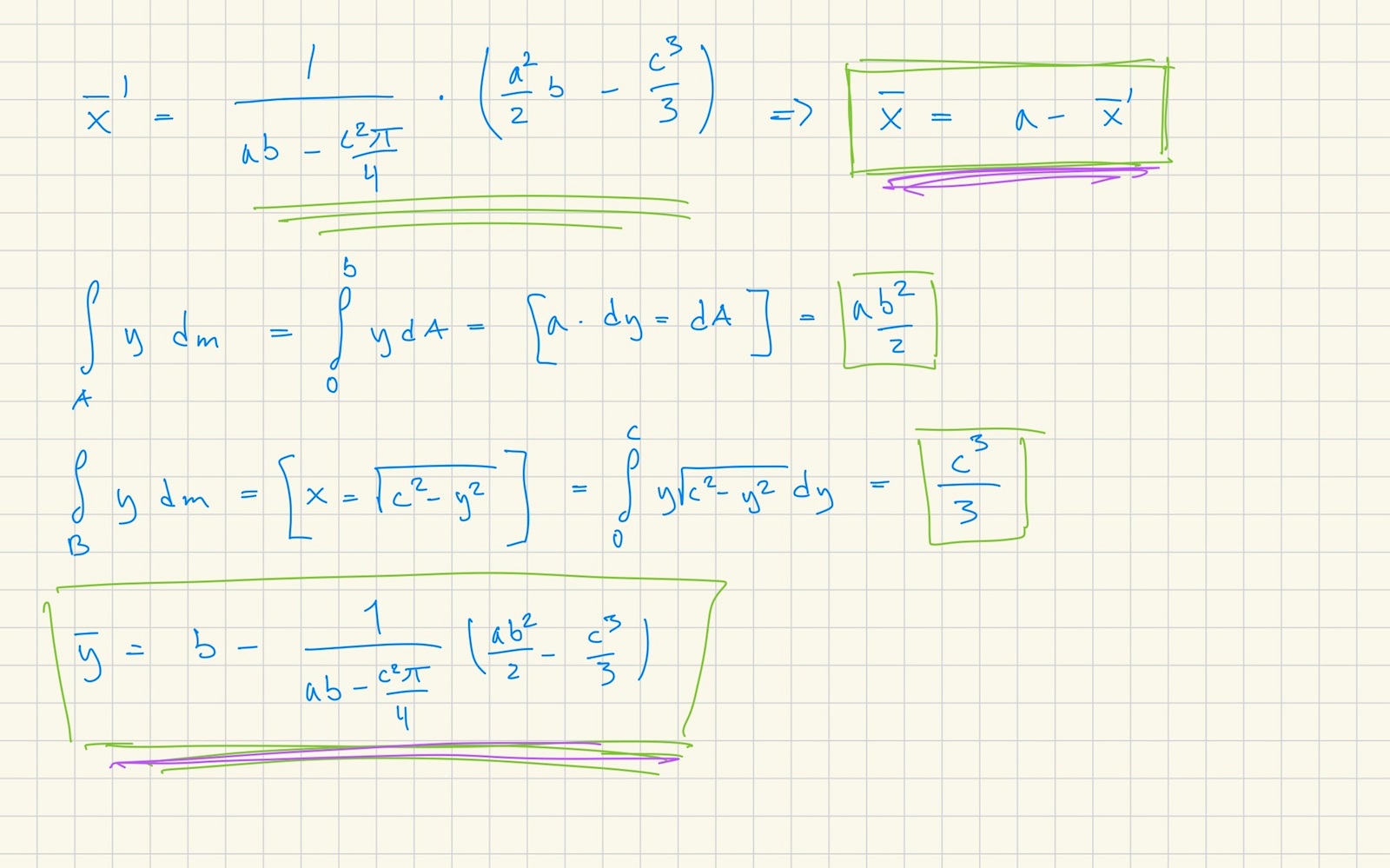
Asså jag får huvudverk, varifrån får du dessa formler?

 $\frac{1}{m_A-m_B}\times ({\int }_{A}x dm - {\int }_{B}x dm)$

Liksom hur ska jag veta det här? Det känns inte intuitivt och jag vill inte använda något som jag inte förstår. 

Vänta det är nog bara som den vanliga formeln egentligen x=(∫xdA)/A fast den räknar ut det direkt, alltså om man hade typ flera hål eller något så hade man kunnat fortsätta lägga till massa - m_c - m_d etc och vice versa för integraler.

Okej vänta så vid ${\int }_{A}x dm = (a^2/2)*b$, så bytte du ut (i mellansteget) dA med b*dx. Känns som det behövs en indikator där.

Okej så ${\int }_A$ är bara ett sätt du betecknar (tyckte det kändes konstigt utan övre gräns på integral).

Sen på ekvationen därefter gjorde samma att du bytte ut igen för vad både dA och y var och sen stoppade in. Sen fick du en helt ny variabel från någonstans, t, och vad t är var något du kom på för att få bort x från integralen. 

Sen valde du vad du ville att dt skulle vara så att det blev lämpligare senare i ekvationen, alltså du tänker i förväg. 

Sen hänger jag inte med igen. x = c och sen så vridde du och vände på hela integralgränsen, har ingen aning hur du gjorde eller tänkte där men okej. Sen så stoppade du bara in vad du fick.

Grundprincipen: få fram rätt formeln, använd någon metod för det finns flera, få bort x och dA, dM, dV whatever man har, och på något sätt fippla med integraler så det blir rätt. Ber om ursäkt om det låter taskigt men det här är svårt för mig. 

Missat att svara på denna. Löste det sig? Formlerna är från boken och Ulfs föreläsningar. Men du verkar ha förstå det mesta. Det handlar om att man använder en area-densitet (kg/m^2) som multiplicerar med en areaintegral blir en massa.

MrPotatohead skrev:

Missat att svara på denna. Löste det sig? Formlerna är från boken och Ulfs föreläsningar. Men du verkar ha förstå det mesta. Det handlar om att man använder en area-densitet (kg/m^2) som multiplicerar med en areaintegral blir en massa.

Ja det löste sig, gäller bara att komma ihåg hur man gör sen. Det största tricket imo var att vrida på hela figuren så att kvartscirkeln var vid origo, visste inte att man fick göra det. Jag missade en av Ulfs föreläsningar och det var då han förmodligen gick igenom detta. Det var också något annat moment om att skulle kompensera. T.ex. om man flyttade en kraft skulle man se till att vridmomentet och totalkraften var det samma i systemet. Ska vara helt ärlig, vet inte riktigt hur man gör på sådana än.

Kanske en bra träning i integrering. Men det kommer bli väldigt lättare med flervarre. 

MrPotatohead skrev:

Kanske en bra träning i integrering. Men det kommer bli väldigt lättare med flervarre. 

Jag brukar inte gå på de föreläsningarna heller, känns överväldigande ofta lol. Chilla jag menar fortsättnings analysen.