Mekanik 1 - Skärningspunkt För Resulterande Kraft
Jag fattar inte hur jag ska få fram var den verkningslinjen skär. Metoder som jag känner till är:
1. använd enhetsvektor, multiplicera med k så den blir godtyckligt stor så vi får en linjens ekvation, skapa en annan linje vid x-axeln (y=0), beräkna algebraiskt när ekvationerna är lika. Problemet är att vi inte har vektorn och dess koordinater, utan bara den resulterande kraftens längd.
2. Använd baserna (i hatt, j hatt och k hatt) och sen projicera på något vänster.
Räkna ut kraftsystemets moment map origo. Var skall man placera den resulterande kraften på x- respektive y-axeln för att få samma moment map origo?
PATENTERAMERA skrev:Räkna ut kraftsystemets moment map origo. Var skall man placera den resulterande kraften på x- respektive y-axeln för att få samma moment map origo?
Vet inte ens om jag räknade ut kraftsystemets moment map origo rätt. Jag fick:
M = rcos(a2)T2 - rcos(a1)T1.
Men grejen är att det finns en x-komponent till T1 som kanske också bidrar. För T2 så bidrar dess x-komponent med 0 vridmoment då den är parallell med x-axeln efter att ha förflyttat längs dess verkningslinje.
M = r(T1 - T2)ez.
PATENTERAMERA skrev:M = r(T1 - T2)ez.
Jag fattar fortfarande inte. Jag fattar inte hur du kom fram till det, tankegång eller vad ez är
Det är enhetsvektor i z-led.
Den effektiva hävarmen för T1 är r. Och kraften vrider moturs. Moment i z-riktningen enligt högerhandsregeln.
Den effektiva hävarmen för T2 är också r och vridningen är medurs. Moment i negativa z-riktningen.
PATENTERAMERA skrev:
Wow det här är en jättebra bild, tack så mycket för förtydligandet. Ska bara tänka lite på det så det blir rätt också!
PATENTERAMERA skrev:M = r(T1 - T2)ez.
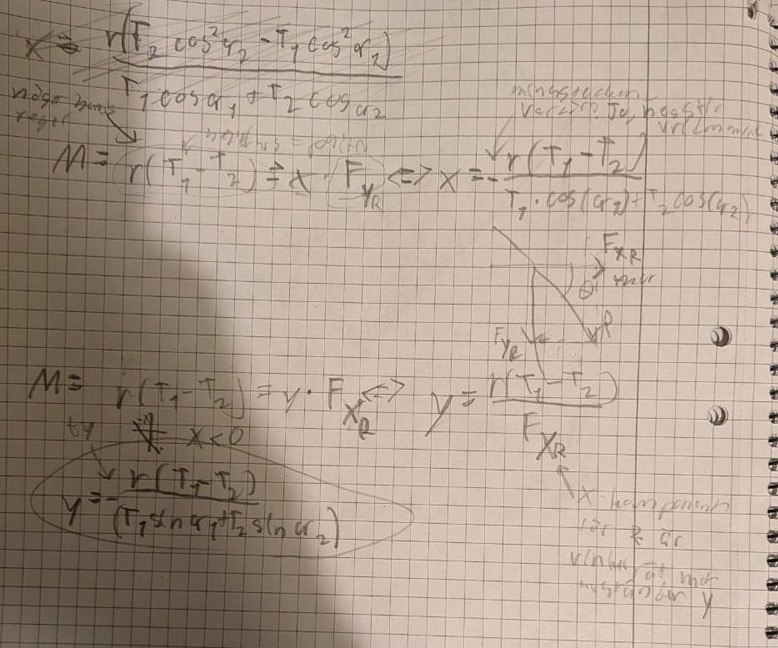Så nu löste jag det och förstod hur du tänkte. Jag försökte göra någon trigonometrisk beräkning med den bilden du skickade där jag förlängde T1 och T2 tills de nådde x-axlarna och sen beräknade avståndet men det var för komplicerat.
Så jag kollade mer på din M = r(T1 - T2)ez. Mycket bättre eftersom det är vinkelrät, det anger alltså det TOTALA vridmomentet så man behövde inte vidare bryta ner T1 eller T2 till dess x och y komponenter som jag försökte. Det med ez också är att ja det är den basen men man behövde inte ta med det eftersom det bara är en punkt det handlar om, origo (och utan z-led).
Sen använde jag formeln för vridmoment för x och y axeln, bröt ned till den vinkelräta kraften (som fås från totala kraften och trigonometri beräkning).
Till sist tog jag till hänsyn om vridmomentet var positivt eller negativt enligt högerhandsregeln (vilket är därför du tog med ez).
Tack så mycket! Det var inte så jag förväntade mig att man beräknade sådana här uppgifter men intressant :)
