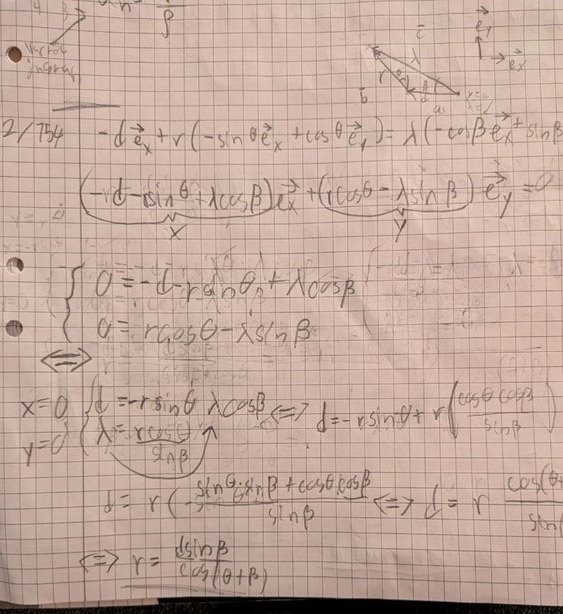14 svar

84 visningar

Sykey behöver inte mer hjälp

Mekanik 1 - Vridande armatur

Jag har två frågor

1. Går det använda cosinussatsen på denna eller övertänker jag? Då fick jag en tid som jag måste få bort. Se jag vet inte riktigt hur man deriverar m.a.p vinkel, det är lite nytt.

2. Om man använder tangentiell och normalbas (e_r och e_$θ$). så förstår jag inte vilken rikting e_$θ$ ska vara. Liksom e_r är ju i samma riktning som radien men e_θ kan ju antingen gå höger eller vänster. Hur ska man veta? Båda hållen är ju vinkelräta.

Sykey skrev:

Jag har två frågor

1. Går det använda cosinussatsen på denna eller övertänker jag? Då fick jag en tid som jag måste få bort. Se jag vet inte riktigt hur man deriverar m.a.p vinkel, det är lite nytt.

2. Om man använder tangentiell och normalbas (e_r och e_$θ$). så förstår jag inte vilken rikting e_$θ$ ska vara. Liksom e_r är ju i samma riktning som radien men e_θ kan ju antingen gå höger eller vänster. Hur ska man veta? Båda hållen är ju vinkelräta.

r' ska vara i termer av v, beta, theta

r'' ska vara i termer av v, d, beta, theta

$θ$ '' ska vara i termer av v, d, beta, theta

$- d {\vec{e}}_{x} + r (- \sin θ {\vec{e}}_{x} + \cos θ {\vec{e}}_{y}) = λ (- \cos β {\vec{e}}_{x} + \sin β {\vec{e}}_{y})$ .

Vilket ger att $r = \frac{d \sin β}{\cos (θ + β)}$ .

PATENTERAMERA skrev:

$- d {\vec{e}}_{x} + r (- \sin θ {\vec{e}}_{x} + \cos θ {\vec{e}}_{y}) = λ (- \cos β {\vec{e}}_{x} + \sin β {\vec{e}}_{y})$ .

Vilket ger att $r = \frac{d \sin β}{\cos (θ + β)}$ .

Nej, jag fattar inte denna uppgiften. Jag fattar heller inte hur du fick bort lambda. Vi vill ha förändringstakten r' angett i v, beta, theta. Ge inte svaret direkt, vill mestadels veta hur man tänker. Asså ren huvudverk nu asså. Tog en kopp kaffe kl 02:20, tror jag går vidare för tillfället istället.

Du har två obekanta, r och lamda. Två ekvationer (x-led och y-led). Lös ut r.

Sedan har vi med tex polära koordinater att

$\dot{r} {\vec{e}}_{r} + r \dot{θ} {\vec{e}}_{θ} = v \vec{e}$ . Här är $\vec{e}$ en enhetsvektor som beskriver pistongens riktning.

PATENTERAMERA skrev:
Du har två obekanta, r och lamda. Två ekvationer (x-led och y-led). Lös ut r.

Sedan har vi med tex polära koordinater att

$\dot{r} {\vec{e}}_{r} + r \dot{θ} {\vec{e}}_{θ} = v \vec{e}$ . Här är $\vec{e}$ en enhetsvektor som beskriver pistongens riktning.

Jag prövade x=-rsin $θ$ och y=rcos $θ$ ,. r togs u.

Jag prövade x=d och då behövde y vara 0. Fick $r = \frac{d \sin β}{\cos β \cos θ}$

Jag prövade till slut x=0 och y=0 och då fick jag ditt värde för r:

$r = \frac{d \sin β}{\cos (θ + β)}$

Tog du x=0 och y=0 för det skulle bli enklast att jobba med? Det förra r jag fick borde väl också funka? Man kan ju få flera olika ekvationer för r.

Okej men nu vet jag varifrån r kommer. Nu vill vi ha $\dot{θ}$ , och dessutom vill vi ha r' i termer utan d och istället med v.

Det som är lite otydligt i patenterameras lösning (tog mig, med min sega hjärna, lång tid till att förstå) är att hen sätter upp en (vektor)ekvation för punkten/vektorn A med origo i O först uttryckt i d (VL) och sedan i $\lambda$ (HL).

förstår jag inte vilken rikting $e_\Theta$ ska vara

Jag tror att riktningen inte spelar någon roll så länge man håller sig till 2 dimensioner. Men man måste alltid vara noga med att följa det koordinatsystem som man har bestämt sig för.

PATENTERAMERA skrev:

Har du förflyttat bilden så att svansen till a och c ligger i O?

Edit: Okej men vi har r, sen ville vi ha r' så jag deriverade r och då fick jag r'=-(d*sinB)/(sin( $θ$ +B)... Jag kan ha deriverat r fel.

PATENTERAMERA skrev:

men hur är det -de_x och inte +de_x (samma med -cos B e_x )_, då går vi ju åt vänster, blir inte vektorerna omvända annars? Jaha nej vänta va, så vi har längden d, vi gångrar med -e_x för att gå vänster precis som vektorn a gör och vi behöver inte ens utgå från origo, alltså vektorn a börjar inte i origo (utan spetsen hamnar där istället). Jag trodde det var det som vara hela grejen med att ha en bas (e_x och e_y). Aja okkk.

Jag har definierat ${\vec{e}}_{x}$ åt höger - se figuren.

PATENTERAMERA skrev:
Jag har definierat ${\vec{e}}_{x}$ åt höger - se figuren.

Ja jag såg det men basen utgår alltid från origo (O) i detta fall så jag trodde att när du skrev -de_x så går vi åt vänster (vilket a gör) men också att svansen för a och skulle hamna vid origo.

Jag börjar ana att det är 1 som är rätt sätt att tänka då. Så man utgår från origo Aha vänta och då är det v_rvi vill ha vilket vi löser ut från

v²= $v_{r}^{2} + v_{θ}^{2}$ ,

Kan man då använda vanlig trigonometri för att få fram att v $θ$ =cos(B+θ), vi kör på det.

Men jag fattar inte, även om vi har hastighetens ekvation för polära koordinater så vill vi inte ha med e_r och e_{$θ$ .}Så de måste försvinna, jag trodde bara vi behövde derivera vårat r så skulle vi få svaret utifrån ekvationen för polära koordinater men då måste vi får bort d och också få med v. Även om vi deriverar m.a.p d så får vi bort variabeln d från ekvationen för r men då behöver vi ett v.

Edit trigonometri funkade.

Så:

$v = \overset{}{\dot{r} e_{r} + r \dot{θ e_{θ}}} \Rightarrow v_{r} = \dot{r} T r i g o n o m e t r i v_{r} = v \sin (β + θ)$

Den sista ekvationen är rätt också. Asså wow denna är tuff helt ärlig, men det de ville ha är förändringstakten av r, inte den där vektorekvationen men man ENBART hur snabbt r ändras. Tack så hemskt mycket för hjälpen även om jag kanske är irriterande lol.

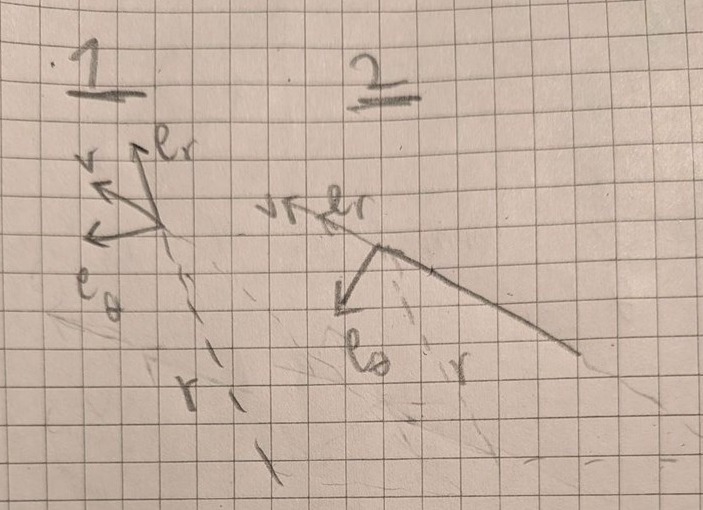
Edit: wait a minute, did I even use what we got for r or did we just use trigonometry?

Tack så mycket för hjälpen, hade inte klarat det utan din hjälp! Min redovisning ser dålig ut men får försöka bli bättre på det.

Svara

Visa senaste svar