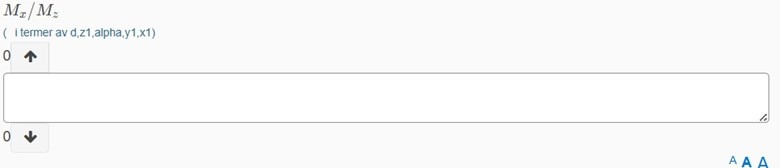
Mekanik 1 - Vridmoment Mx/Mz (Fysik/Universitet)

Det var det tag sedan du ställde frågan. Har du fått ordning på den?

Peter skrev:
Det var det tag sedan du ställde frågan. Har du fått ordning på den?

Nej och jag försökte igen och jag tycker den "klumpig"/mycket att hålla reda på. Liksom när det står Mx så går det att lägga kraften T precis vid punkten B så får man fram dess kraft komponenter. Vid punkten B så hade då komposanten Tz spelat roll om man förflyttat den lite till att vara precis under x-axeln. Avståndet till Tz hade varit $d \sin (α)$ . Det jobbiga är dock att beräkna vad Tz blir för det är så många vinklar och mått och sen så är det inte origo heller sen.. Så för att beräkna vinklarna för BC börjar vi med z-komponenterna, och då är avståndet i z-ledet z1-dcos(alpha), avståndet i x-led x1 och avståndet i y-led y1+dsin(α). Sen får man fram två hypotenusor, en som är sträckan för BC och en som är dess projektion basically, då får man två vinklar där, sen ska man ta de vinklarna och gångra med T (som typ motsvarar hypotenusan/sträckan BC) för att få de olika kraftkomponenterna. SEN efter allt det här ska man beräkna vridmomentet, och sen även dela dem med varandra och samtidigt ska man hålla kolla på vad som tar ut varandra och inte. Asså det är lite för mycket för min smak.

Ja mycket vinklar är det men jag tror att du slipper det mesta men inte allt om du beräknar momentet kring O med en kryssprodukt, se länk nedan (antar/hoppas att ni har gått igenom det) och behandlar momentet som en vektor. Då behöver du inte dela upp momentet i komposanter. Vid O måste det finnas ett motriktat moment eftersom det är jämvikt. Det bökigaste då, är att ta fram koordinaterna för kraften T (sätt origo t.ex vid O). Men det är "bara" geometri. Sen återstår "bara" kraften vid O. Den får du via kraftjämvikt för röret.

Kolla denna: https://share.google/Fmvx23zOeBiw2Iqu4

Peter skrev:
Ja mycket vinklar är det men jag tror att du slipper det mesta men inte allt om du beräknar momentet kring O med en kryssprodukt, se länk nedan (antar/hoppas att ni har gått igenom det) och behandlar momentet som en vektor. Då behöver du inte dela upp momentet i komposanter. Vid O måste det finnas ett motriktat moment eftersom det är jämvikt. Det bökigaste då, är att ta fram koordinaterna för kraften T (sätt origo t.ex vid O). Men det är "bara" geometri. Sen återstår "bara" kraften vid O. Den får du via kraftjämvikt för röret.

Kolla denna: https://share.google/Fmvx23zOeBiw2Iqu4

hmm, intressant, vi hade tenta på mekaniken och det kom en sådan uppgift där de hade skrivit om vridmomentet som en rak pil och jag var chockad för jag är så van med att pilen för vridmoment alltid är böjd. Så nej jag har inte sett det man ska kolla på det nu då.

Edit: Jag har nu läst hela och förstod hyfsat, ska pröva på uppgiften men jag fattar inte en sak: HUR? Kraften går åt ett hål och sen vridmomentet ett helt annat håll, det känns inte intuitivt rätt. I dokumentet tog de upp ett exempel med vridmomentets verkan kan tolkas genom att om man hade haft en skruvmejsel i riktningen av M_o (så spetsen är där M_o slutar, alltså dess storlek) och vrider enligt högerhandsregeln. Jag trodde att vridmomentets verkan var M_o som vi just fick fram?

Det funkade, och det funkade jättebra, man kunde välja en radie och en godtycklig punkt så jag förflyttade kraften T längs dess verkningslinje upp till punkten C och då blev x-koordinaten 0. Då kunde jag få fram radien i vektor form (med basen e_x, e_yoch e_z). T komposanterna fås ut genom geometri beräkning.

DÄREMOT så stötte jag på två problem:

1. Riktningen på kraften, jag vet inte men man kanske måste kolla på figuren för att se om komposanten är negativ eller inte för det känns inte som att det löser sig vanligtvist annars. Det är viktigt för det påverkar även vad det blir för vridmoment. När ska man hålla koll på tumregeln också? Det har varit ett par gånger jag fått fel på riktningen av vridmomentet.

2. Ser du (-dcos(α)+z1) som jag skrivit? Först skrev jag (dcos(α)-z1) för jag trodde att den skulle vara längre och man tar ju alltid störst minus mindre men uppgiften gjorde motsatsen. Alltså problemet är: Hur ska jag veta vilken som är mindre; z1 eller dcos( $α$ )

Kraften går åt ett hål och sen vridmomentet ett helt annat håll

Det är egentligen mest en konvension men den visar sig vara lite användbar i beräkningar. Logiken är att när något roterar så finns det en rotationsaxel. Låt oss då representera t.ex. momentet (i det här fallet) med en vektor längs denna axel. Positiv riktning längs axeln har man sagt ska följa högerhandsregeln (eller skruvmejsel), precis som kryssprodukter. Man kallar det för en pseudovektor. Det är inte bara vridmoment (torque i länken) som kan beskrivas av pseudovektorer.

jag förflyttade kraften T längs dess verkningslinje upp till punkten C

Ett utmärkt val!

Hur ska jag veta vilken som är mindre; z1 eller dcos(α)

Det framgår inte så det kan man inte veta. Om koordinatsystemet ska vara högerorienterat (vilket man "alltid" ska eftersträva) så pekar z-axeln åt vänster i bilden. Så här kan du tänka när det gäller tecknet på $T_{z}$ (eller $F_{z}$ som du kallar den): Om $z_{1} > d\cos\alpha$ så ska $T_{z} > 0$ . Det betyder att $T_{z} = z_{1} - d\cos\alpha$ annars blir det fel tecken. Glöm det där med att subtrahera mista från största. Om $z_{1} < d\cos\alpha$ så blir $T_{z} < 0$ och det stämmer ju med riktningen på z-axeln.

Peter skrev:

Kraften går åt ett hål och sen vridmomentet ett helt annat håll

Det är egentligen mest en konvension men den visar sig vara lite användbar i beräkningar. Logiken är att när något roterar så finns det en rotationsaxel. Låt oss då representera t.ex. momentet (i det här fallet) med en vektor längs denna axel. Positiv riktning längs axeln har man sagt ska följa högerhandsregeln (eller skruvmejsel), precis som kryssprodukter. Man kallar det för en pseudovektor. Det är inte bara vridmoment (torque i länken) som kan beskrivas av pseudovektorer.

jag förflyttade kraften T längs dess verkningslinje upp till punkten C

Ett utmärkt val!

Hur ska jag veta vilken som är mindre; z1 eller dcos(α)

Det framgår inte så det kan man inte veta. Om koordinatsystemet ska vara högerorienterat (vilket man "alltid" ska eftersträva) så pekar z-axeln åt vänster i bilden. Så här kan du tänka när det gäller tecknet på $T_{z}$ (eller $F_{z}$ som du kallar den): Om $z_{1} > d\cos\alpha$ så ska $T_{z} > 0$ . Det betyder att $T_{z} = z_{1} - d\cos\alpha$ annars blir det fel tecken. Glöm det där med att subtrahera mista från största. Om $z_{1} < d\cos\alpha$ så blir $T_{z} < 0$ och det stämmer ju med riktningen på z-axeln.

Jag hänger fortfarande inte med krafterna och tecknet. En axel sträcker sig åt båda hållen.

Jag kan vara med på detta: Om z1 > dcos så måste Tz vara positivt. Ahh kolla man kan fortfarande tänka så med största och minsta.

Fall 1: z1 > dcos ==> Tz > 0

Tz = $T * \frac{z_{1} - d * \cos α}{c_{1}}$ , alltså positivt

Fall 2: z1 < dcos ==> Tz < 0

Tz = $- T * \frac{d * \cos (α) - z_{1}}{c_{1}}$ $= T * \frac{z_{1} - d * \cos (α)}{c_{1}}$

Så Tz blev samma sak oavsett genom att lägga till minus tecken på kraften om den var riktad åt negativa hållet.

Okej men vad det gällde tummen. Så om tummen sammanfaller med positiv riktning på rotationsaxeln så är det positiv vridmoment. Okej men om den är riktat motsatt håll då, då vrider jag bara min tumme åt andra hållet och så funkar det lika bra. Så då måste man hålla koll på vad positiv riktning på rotations axeln är då eller bara de fixa axlarna (x,y,z). Jag hänger inte riktigt med ngl.

Så Tz blev samma sak oavsett

Precis, matten ger dig rätt riktning oberoende av vilken som är störst. Det viktiga är att du subtraherar "åt rätt håll".

hålla koll på vad positiv riktning på rotations axeln

Riktningen på momentet ges av kryssprodukten. Kom ihåg att ordningen spelar roll i en kryssprodukt (den är antikommutativ). Använd högerhandsregeln för att se vilket håll kryssprodukten (momentet I det här fallet) pekar.

Alltså:

$\vec{M} = \vec{r} \times \vec{T} = - \left(\vec{T} \times \vec{r}\right)$

Allt bygger på att du har ett högerorienterat koordinatsystem.

Peter skrev:

Så Tz blev samma sak oavsett

Precis, matten ger dig rätt riktning oberoende av vilken som är störst. Det viktiga är att du subtraherar "åt rätt håll".

hålla koll på vad positiv riktning på rotations axeln

Riktningen på momentet ges av kryssprodukten. Kom ihåg att ordningen spelar roll i en kryssprodukt (den är antikommutativ). Använd högerhandsregeln för att se vilket håll kryssprodukten (momentet I det här fallet) pekar.

Alltså:

$\vec{M} = \vec{r} \times \vec{T} = - \left(\vec{T} \times \vec{r}\right)$

Allt bygger på att du har ett högerorienterat koordinatsystem.

Hmm det där är ett mycket tydligare sätt som du skriver vridmoment på också. Så man byter alltid tecken om man byter position på hävarmen och kraften, uppfattat.