mekanik

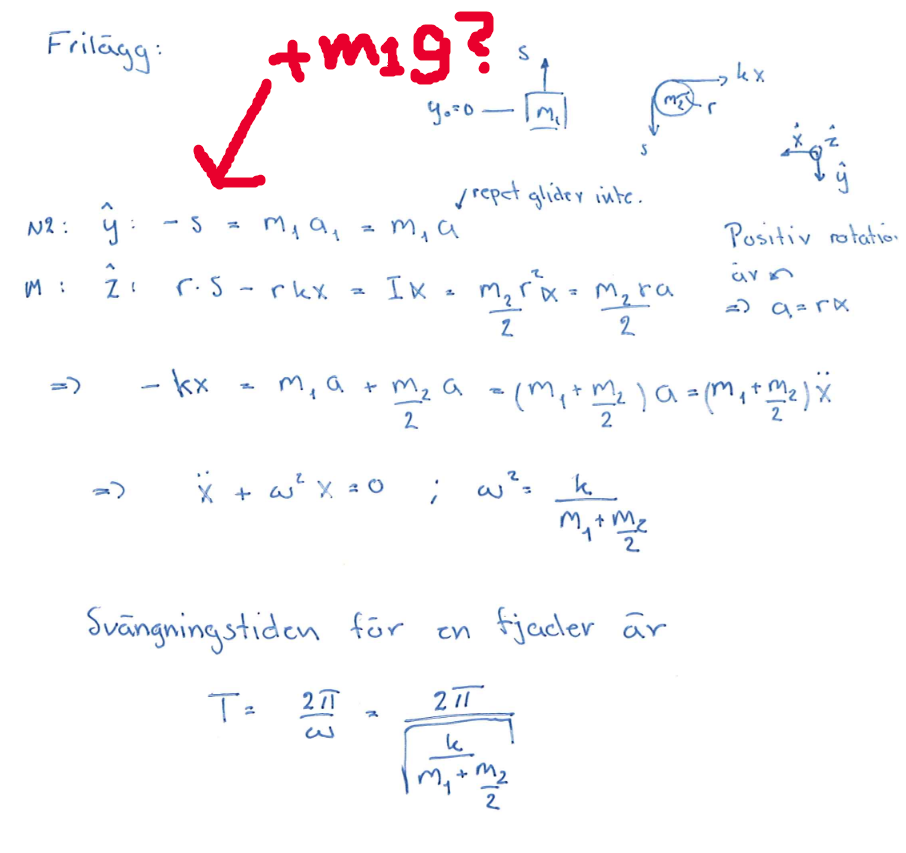
Det verkar ju vara ett opedagogiskt lösningsförslag, men ibland gör man så för harmoniska svängningar eftersom jämviktstermerna ändå tar ut varandra.

Om du vill kan du räkna med $m_1g$ i den första ekvationen och tänka på att fjädern då måste ha en jämviktsspänning $kx_0$ i den andra ekvationen. Alltså

$m_1g-s=m\ddot{x}$ (Newton II)

$-k(x_0+x)r+sr=I\alpha$ (Rörelsemängdsmomentet, $\tau=I\alpha$, $\ddot{x}=r\alpha$)

För jämvikt (när vikten hänger stilla) gäller $m_1g=kx_0$.

D4NIEL skrev:

Det verkar ju vara ett opedagogiskt lösningsförslag, men ibland gör man så för harmoniska svängningar eftersom jämviktstermerna ändå tar ut varandra.

Om du vill kan du räkna med $m_1g$ i den första ekvationen och tänka på att fjädern då måste ha en jämviktsspänning $kx_0$ i den andra ekvationen. Alltså

$m_1g-s=m\ddot{x}$ (Newton II)

$-k(x_0+x)r+sr=I\alpha$ (Rörelsemängdsmomentet, $\tau=I\alpha$, $\ddot{x}=r\alpha$)

För jämvikt (när vikten hänger stilla) gäller $m_1g=kx_0$.

Tack ska du ha Daniel!