Mekanik: att projicera vridmoment på annan axel
Hej, se denna:
Visa spoiler

Jag har några frågor:
- Sist står det att förklara innebörden av tecknet i det slutgiltiga svaret (som är negativt). Jag tänker att det naturliga vridmomentet är normal till planet och pekar bort från hyllan (pga högerregeln). Vektorn BC pekar åt motsatt håll mot planets normal, så därför blir projektionen negativ. Men den fysikaliska innebörden? Vad är det?
- Och jag har en till fråga, varför är inte svaret ? Som svaret står i boken är det en skalär när vridmoment måste vara en vektor (?).
- Jag har svårt att greppa situationen här. På föregående sidor illustreras virdmoment med skiftnyckel som håller fast en bult eller liknande. Då är bulten momentpunkten (en punkt) och skiftnyckelns handtag hävarmen (en vektor), men i denna situation är ju skiftnyckeln utbytt mot en planka som inte sitter fast i en punkt utan i en linje? Det står att momentpunkten kan väljas godtyckligt på linjen BC, varför? Vad blir hävarmsvektorn som vi inte väljer B?
Som jag kommer ihåg var detta i vår mekanikbok helt enkelt en definition.
Momentet map en axel med riktning e definierades som momentet map någon punkt på axeln skalärmultiplicerat med vektorn e. Du får naturligtvis samma värde oavsett vilken punkt på axeln du väljer, annars hade det inte varit en speciellt bra definition.
Tecknet beskriver i vilken riktning kring axeln som kraften tenderar att vrida dörren. Ta högerhanden och tummen längs e och krök resten av fingrarna. Om tecknet är positivt är vridningen i fingrarnas riktning, annars i motsatt riktning.
Tack, jag förstår, men har du ett svar på min andra fråga? I resten av kapitlet och i övningsfrågorna är vridmomentet en vektor, inte en skalär.
Jag hittade denna: https://physics.stackexchange.com/questions/349962/moment-of-a-force-about-a-given-axis-torque-scalar-or-vectorial
Men deras svar duger inte för mig, det finns både komponenter och vektorkomponenter, vi kan minst lika gärna låta vridmomentet längs en axel vara dess vektorkomponent längs axeln. Jag ser ingen anledning varför det inte är det!
Ja, vi har således att göra med två definitioner. Vridmomentet av en kraft med avseende på en punkt och med avseende en axel med riktning e. Notera att i definitionen av det senare utnyttjar det tidigare konceptet.
Men min fråga är varför?
Det är ju svårt att veta exakt varför textboksförfattare väljer sina definitioner på det ena eller andra sättet - jag är inte tankeläsare. Men i detta fall så kan man väl gissa att en skalär storhet är enklare att tolka, det ger direkt en tydlig indikation om hur mycket kraften tenderar att vrida luckan kring upphängningsaxeln. Om du istället gav en vektor tex (2, 7, -3) (Nm) så ger det inte alls samma tydliga insikt.
Tur att författaren och min lärare är samma person! Detta ska jag fråga honom.
Jag förstår... men iförsig går det fortfarande att skriva , alltså undvika att skriva ut basvektorns komponenter.
Jag har inte kommit längre än exakt den sidan jag la upp, men om man behöver addera vridmoment längs olika axlar går det ju inte att ha kvar de som skalärer.
Eftersom läroböckerna från 80-talet hade samma definition så har väl detta hängt med ett tag, och författaren kände väl inte något behov att revolutionera utbildningsväsendet. Jag misstänker att saker kommer se lite annorlunda ut när du blir professor.
Men berätta gärna vad läraren säger om saken.
Det kanske är en petsak egentligen, men jag ska fråga!
Som du kanske vet började jag på teknisk fysik, och det med mer än ett år rostiga fysikkunskaper från gymnasiet. Jag lär få kompromissa med den matematiska strängheten en del framöver.
Det skulle mycket väl kunna vara så att man byter mellan att betrakta den som skalär och vektor beroende på situation och att jag hakar upp mig.
- Den fysikaliska innebörden är att kraften utövar ett moment kring BC-axeln som gör så att luckan ABCD inte roterar på grund av tyngdkraften. Om du stoppar tummen i BC riktningen ser du med högerhandsregeln i vilken riktning en tyngdkraft skulle rotera luckan.
- Ett moment är en skalär om det uttrycks med avseende på en axel eftersom riktningen är underförstådd (tecknet är den enda binära riktningsinformation som behövs). Att addera moment kring olika axlar förekommer väldigt sällan. Vanligt är att reducera det till och hantera det tvådimensionellt inom mekanik även om situationen är tredimensionell.
- Ponera att du väljer enhetsvektorn istället. Den vektorn kan byggas upp av vektorn och men kommer inte ha något bidrag relativt axeln eftersom den är parallell med axeln du projicerar momentet på. Du kan även bevisa för dig själv att oavsett vilken punkt på axeln du väljer kommer det resulterande momentet ha storleken som ges av det vinkelräta avståndet mellan axeln och kraften.
Tack så mycket för dina svar!!
Har du ett någorlunda realistiskt exempel där man behöver addera vridmoment kring axlar? Jag känner inte till mekanik så bra, jag har ingen bra fantasi heller.
Inom statik söker man statisk jämvikt vilket ger följande relationer:

Detta innebär rent praktiskt att du antingen kan titta på plan normala till varje axel i ett ortogonalt koordinatsystem och summera moment eller göra det vektoriellt i tre dimensioner direkt.
Då verkliga mekaniska situationer nästan alltid innehåller redundans och statisk obestämbarhet krävs ofta knep, reduceringar och kloka förenklingar för att systemen ska vara lösbara. Statisk obestämbarhet är när du har fler okända än ekvationer i ditt resulterande ekvationssystem. Något som tvådimensionell reduktion kan hjälpa med.
Typiska problem i tre dimensioner där vektorsumman är att föredra är som denna:
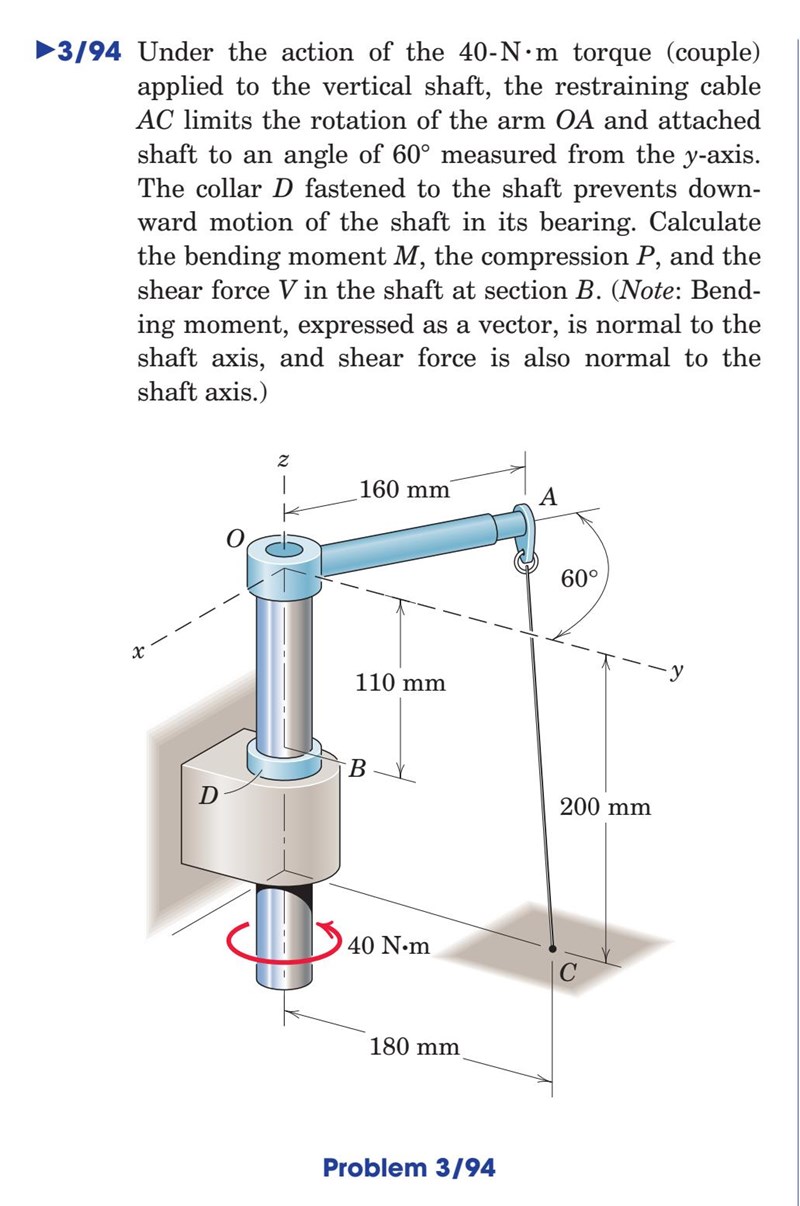
Även inom dynamiken kan det vara högst användbart att veta resulterande moment kring en specifik axel när du vill veta vilken påfrestning en detalj utsätts för. De yttre momenten kan därmed summeras relativt en specifik axel genom att först räkna ut totala momentet och sedan projicera det på en axel. Sedan kommer du också lära dig om Newtons generaliserade andea lag och den förändring av rörelsemängdsmoment som ett resulterande moment ger upphov till. I dynamisk analys kan detta vara ganska viktigt i vissa specifika situationer.
Den där konstruktionen var lite komplicerad, kan du se om jag förstår rätt?
Staven utsätts för två vridmoment, en underifrån (från någon annan okänd konstruktion) med 40Nm, och den vridvektorn är parallell med staven. Det andra vridmomentet orsakas av en kraft längs AC via hävarmen OA? Den är normal till planet OAC?
Dessa två ickeparallella vridmoment ska adderas?
Du har ett böjmoment vid B också som är en reaktion på trådkraftens moment.
Du har alltså ett moment från trådkraften som bidrar till att motverka det yttre momentet så att men även två moment i x- och y-led som orsakar en reaktion i fästet i form av ett böjmoment. Detta böjmoment är då .
Edit: Du har helt rätt i att momentet från trådkraften är normal till planet OAC då det är en kryssprodukt mellan OA och trådkraften som är parallell med AC.
Edit2: Tänkte inte på att förklara närmre men anledningen till att böjmomentet är normalt till z-axeln är för att fästet är format som en glidskena och därför inte kan anbringa moment i z-led.
Förstår!
Och jag gjorde precis en fråga från boken där det krävdes att addera vridmoment, och den var inte så svår!



