Mekanik - cirkelbana
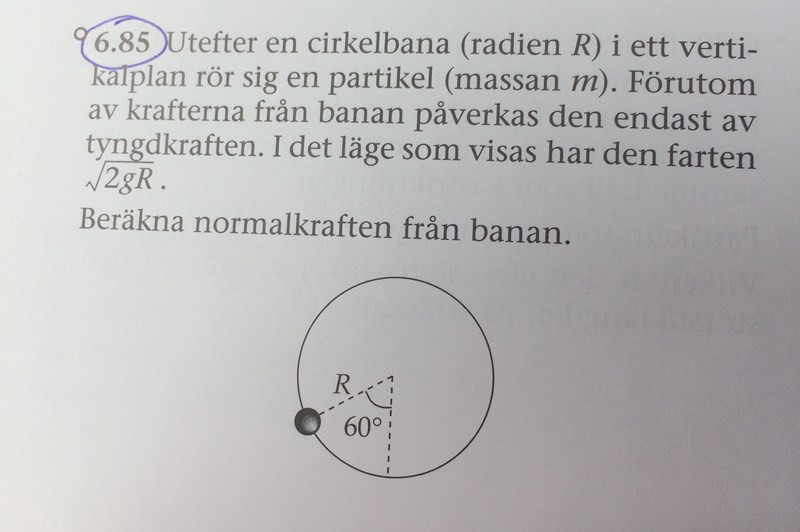
Jag vet inte vad jag gör för fel, för jag får två olika normalkrafter när jag delar upp i x- och y-led. Svaret ska bli 2,5 mg, men jag får 2mg respektive 2,3mg. Jag har bifogat en bild på min lösning nedan.

Förutom centripetalkraften så måste normalkraften kompensera för tyngdkraftens komponent i normalriktningen.
Bo-Erik skrev:Förutom centripetalkraften så måste normalkraften kompensera för tyngdkraftens komponent i normalriktningen.
Okej, jag räknade in tyngdkraften i y-led. Skulle du kunna förklara hur du menar?
Sätt in i uttrycket för centripetalkraften . Tyngdkraften har en komposant med storleken vinkelrät mot banan. Är du med?
Din friläggning är inte korrekt.
Accelerationen är i radiell led, inte i x-led.
I radiell led pekar accelerationen in mot centrum, Normalkraften pekar in mot centrum (som du ritat) och tyngdkraftens komponent i radiell led blir ut från centrum. Newton II (F=ma) i radiell led blir alltså:
Jroth skrev:Din friläggning är inte korrekt.
Accelerationen är i radiell led, inte i x-led.
I radiell led pekar accelerationen in mot centrum, Normalkraften pekar in mot centrum (som du ritat) och tyngdkraftens komponent i radiell led blir ut från centrum.
Jaha då är jag med, tack!


