Mekanik (MOE)

Hur definieras elasticitetsmodulen?

Ebola skrev:

Hur definieras elasticitetsmodulen?

Efter lite research vet jag nu att det är den maximala kraften som ska användas när brott uppstår och den tangenten av kraften vid kompression (tror i varje fall att det är så...) 

Du skrev två olika saker så det är oklart vilken av dem det är du menar.

Elasticitetsmodulen är synonym med styvheten hos materialet och beskriver således lutningen på spänning-töjning-kurvan i det elastiska området (det linjära).

I det här fallet har du en kraft-deformation-kurva vilket medför att du får räkna om lite. Elasticitetsmodulen definieras genom:

$\sigma = E \epsilon$

Där $\sigma$ är spänningen, $\epsilon$ är töjningen och $E$ är elasticitetsmodulen. Ingenjörsspänning är relaterad till kraften som:

$\sigma = F/A_0$

Där alltså $A_0$ är arean innan deformation. Ingenjörstöjning definieras som:

$\epsilon = \Delta L / L_0$

Där alltså $L_0$ är ursprunglig längd innan deformation och $\Delta L$ är förändringen av längden (displacement i din figur). Kombinera dessa storheter och bestäm elasticitetsmodulen genom att ta fram lutningen på kurvan i det elastiska området.

Ebola skrev:

Du skrev två olika saker så det är oklart vilken av dem det är du menar.

Elasticitetsmodulen är synonym med styvheten hos materialet och beskriver således lutningen på spänning-töjning-kurvan i det elastiska området (det linjära).

I det här fallet har du en kraft-deformation-kurva vilket medför att du får räkna om lite. Elasticitetsmodulen definieras genom:

$\sigma = E \epsilon$

Där $\sigma$ är spänningen, $\epsilon$ är töjningen och $E$ är elasticitetsmodulen. Ingenjörsspänning är relaterad till kraften som:

$\sigma = F/A_0$

Där alltså $A_0$ är arean innan deformation. Ingenjörstöjning definieras som:

$\epsilon = \Delta L / L_0$

Där alltså $L_0$ är ursprunglig längd innan deformation och $\Delta L$ är förändringen av längden (displacement i din figur). Kombinera dessa storheter och bestäm elasticitetsmodulen genom att ta fram lutningen på kurvan i det elastiska området.

Det är jag med på, men min fråga är hur jag ska bestämma F, då den varierar. Är det maxkraften man ska använda? 

Ebola skrev:

Du skrev två olika saker så det är oklart vilken av dem det är du menar.

Elasticitetsmodulen är synonym med styvheten hos materialet och beskriver således lutningen på spänning-töjning-kurvan i det elastiska området (det linjära).

I det här fallet har du en kraft-deformation-kurva vilket medför att du får räkna om lite. Elasticitetsmodulen definieras genom:

$\sigma = E \epsilon$

Där $\sigma$ är spänningen, $\epsilon$ är töjningen och $E$ är elasticitetsmodulen. Ingenjörsspänning är relaterad till kraften som:

$\sigma = F/A_0$

Där alltså $A_0$ är arean innan deformation. Ingenjörstöjning definieras som:

$\epsilon = \Delta L / L_0$

Där alltså $L_0$ är ursprunglig längd innan deformation och $\Delta L$ är förändringen av längden (displacement i din figur). Kombinera dessa storheter och bestäm elasticitetsmodulen genom att ta fram lutningen på kurvan i det elastiska området.

Den proportionella gränsen finns ju inte i mitt diagram (likt nedan) och därför vet jag väl inte vart det elastiska området slutar? 

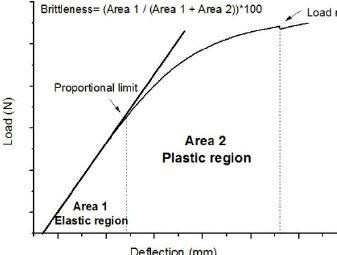
Nej, du är inte med på det jag skrev. Läs igen.

Ta fram lutningen $\Delta F / \Delta L$ och relatera denna till $E$.