Mekanik partikeldynamik

Om mg << kx så kan man försumma den vid m₂. På motsvarande sätt vid m₁. Men det framgår inte av uppgiften att det skulle vara så. Tvärt om är både g och $\theta$ tydligt utsatta i uppgiften så jag förstår inte heller. Kanske fel i facit?

Dämpningsfaktor och period beror inte på statiska krafter då du behandlar dynamisk respons för linjära system. Detta kan du se tydligt genom att definiera koordinaten relativt statiska jämviktspunkten. Det stämmer inte generellt för icke-linjära system men det kommer då framgå från din analys. Har du försökt lösa uppgiften?

Du kan hursomhelst enkelt bevisa detta för dig själv med en fjäder och massa som hänger vertikalt:

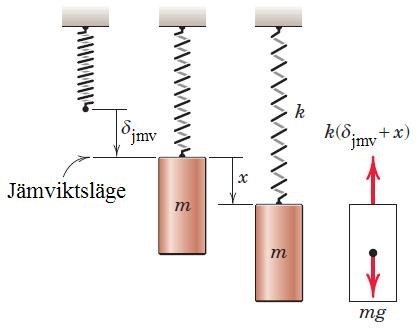Vi får från Newtons andra lag att:

$-k\left({\delta }_{jmv}+x\right)+mg=m\ddot{x}$

Vid jämviktsläget ($x=0$) vet vi att accelerationen är noll och vi får:

$-k\delta_{jmv}+mg=0$

Vi får slutligen:

$m\ddot{x}+kx=0$ vilket ger $\omega_{n} = \sqrt{k/m}$ och $\tau = \dfrac{2\pi}{\sqrt{k/m}}$