Modulo

Hej!

Jag har följande fråga:

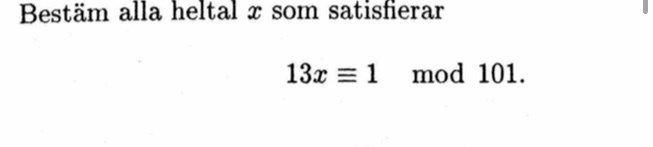
Jag förmodar att det finns någon smart metod för att räkna ut detta så att man inte behöver testa alla x. Vet någon vad det är för metod så kan jag försöka kolla upp den, tack på förhand!

Kongruensekvivalensen betyder att talet 13x ska ha resten 1 vid division med 101. Enligt divisionssatsen finns det heltal x och q så att

$13x=101q+1$

Detta är en linjär diofantisk ekvation. Den löser du enkelt med Euklides algoritm framlänges och baklänges.

Ett alternativt sätt att se på saken är att du söker en multiplikativ invers till 13 (mod101). Alla heltalslösningar ges sedan av $x=(13^{-1})_{101}+101n, n\in \mathbb{Z}$

Svara