Nabla bevis
Tacksam om någon kan förklara hur placerar man nabla...
Upogift;

Lösnikg;
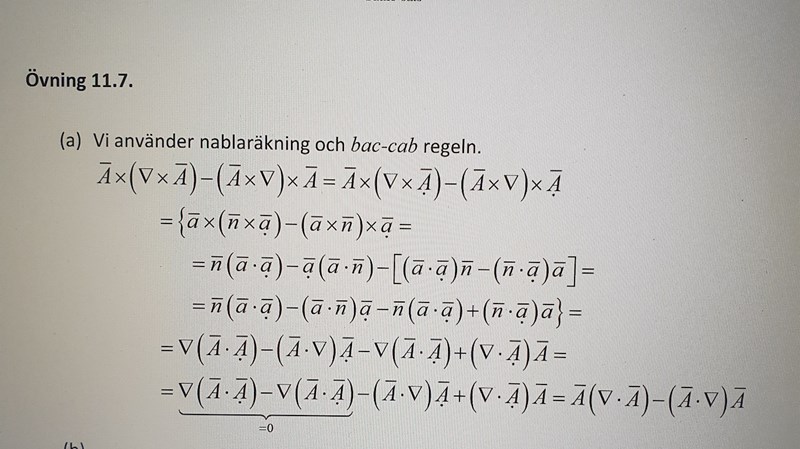
Hej, vad i lösningen är det du tycker är oklart?
Vid nablaräkning använder man operatorn nästan som en vanlig vektor Med betoning på "nästan".
I sitt standardutförande deriverar -operatorn uttryck till höger om sig.
Men ibland vill man kunna förenkla komplicerade produkter mellan vektorer och då behöver man ofta ändra ordningen mellan faktorerna. Ordningen kan dock vara låst av regeln att -operatorn verkar åt höger.
För att komma runt det finns det olika skolor/metoder. Ni tycks använda en prick-notation jag inte sett tidigare. Men prick verkar indikera att vektorn ska nablaseras partiellt samtidigt som andra fält ses som konstanter. Det är helt enkelt ett sätt att hålla ordningen på vilket fält som ska påverkas av nabla, allt annat kan vi gå rakt igenom.
I ditt exempel har man bara bytt tillbaka från till och sedan samlat ihop termerna. Det viktiga är att man när man tar bort prickarna fortfarande har fältet som ska deriveras till höger, så nabla har något att verka på.
Du får vara mer specifikt i vilket steg du inte förstår så kan vi säkert reda ut det.
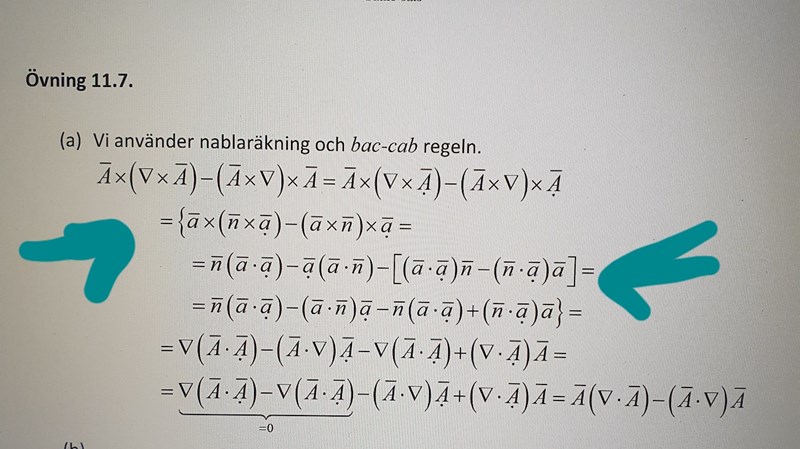 där jag har markerat med pill inom
där jag har markerat med pill inom
[ (a.a)n.......
det blir i nästa rad n(a.a) man flyttade på a men tecknet ändrades inte.
Ahaa ok så det som där A inte har prick betyder att det ser man som konstant. Men varför gör man det?? Man använder ju det som står inom { ...} så det verkar som att man behöver inte änns prickarna.
En till fråga, man säger att nabla är inte vektor så hur påverkar det våra nablaräkning?
Håller med, prick-notationen verkar indikera att vektorn ska opereras på med Nabla operatorn.
Anledningen till att de har skrivit med prickarna i ekvationen inom {} är troligtvis för att du tydligt ska se var termerna hamnar, vilket gör det lättare att applicera denna regel i ditt fall.
Ohh tusen tack ni finns ❤🙏. Åkte till universitetet för att få hjälp av min föreläsare men hittade inte honom.
Vist nabla kan opereras på nabla? så betyder att nabla opereras på båda A och sig själv eller?
Ja, men man får vara lite försiktig. En "minnesregel" som är lurig, men studenter ändå använder är
Eftersom
Men tänk på att t.ex.
I ditt fall kan du använda cyklisk permutation av den skalära trippelprodukten och "minnesregeln":
Jämför hur det blir med det skalära fältet
I min bok det står att man går till index berälning för nabla är begränsad. Hur menar de?
Man använder tensornotation, eller indexnotation.
T.ex kan varje komponent av rotationen uttryckas
Ibland kallar man det också Einsteinnotation efter Albert Einstein.
Ett index som förekommer två gånger summerar man över.
Indexnotation är ett mycket kompakt och effektivt sätt att genomföra beräkningar. Men det krävs att man lär sig räknereglerna.
D4NIEL skrev:Ja, men man får vara lite försiktig. En "minnesregel" som är lurig, men studenter ändå använder är
Eftersom
Men tänk på att t.ex.
I ditt fall kan du använda cyklisk permutation av den skalära trippelprodukten och "minnesregeln":
Jämför hur det blir med det skalära fältet
Hmm vist där hitade du trippelprodukten för att skriva det som ∇⋅(∇×A)=(∇×∇)⋅A=0 , men är det fel att skriva (∇⋅∇)×A = 0 hmm det är fel antar jag
D4NIEL skrev:Man använder tensornotation, eller indexnotation.
T.ex kan varje komponent av rotationen uttryckas
Ibland kallar man det också Einsteinnotation efter Albert Einstein.
Ett index som förekommer två gånger summerar man över.
Indexnotation är ett mycket kompakt och effektivt sätt att genomföra beräkningar. Men det krävs att man lär sig räknereglerna.
Aha ok. Tack för hjälpen!
I am Me skrev:
Hmm vist där hitade du trippelprodukten för att skriva det som ∇⋅(∇×A)=(∇×∇)⋅A=0 , men är det fel att skriva (∇⋅∇)×A = 0 hmm det är fel antar ja
Ja, en annan minnesregel (som återigen bara är en minnesregel) är , vilket är Laplaceoperatorn . Den är skalärvärd (som alla skalärprodukter) och du kan alltså inte bilda en kryssprodukt med den som du skrev.


